RRT*算法的原理简介以及Python实现代码

RRT大致流程
1.初始化随机树tree,以空的随机树开始添加节点,最开始只有Qinit。
2.执行sample函数,在地图中获得一个随机点Qrand。
3.遍历tree中所有节点,找出与Qrand之间代价最小的点Qnearest。
4.执行extend函数,获得Qnearest向Qrand方向上的指定长度的扩展点Qnew。并对Qnew进行碰撞检测,若碰撞检测为真,则结束此次循环,重新选择拓展点。若为假则将Qnearest指定为Qnew的父节点,连接两点之间的连线。
5.判断Qnew是否已经到达指定目标范围,若已经到达,则结束循环,否则继续执行循环知道找到目标范围。
其中sample函数用于,在地图中生成随机点;
def Sample(self, a, b):
Q = [random.randint(0, a), random.randint(0, b)]
return Q
extend函数用于找到拓展点,函数中c为步长。
# 获取Q与最近节点之间的拓展点
def extend(self, a, b, c = 10):
d = [0, 0]
d[0] = a[0] + int(c * (b[0] - a[0]) / math.sqrt((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2))
d[1] = a[1] + int(c * (b[1] - a[1]) / math.sqrt((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2))
return d
整个代码段以输入图片作为地图,以灰度读入作为checkMap,用以碰撞检测;再以正常读入作为drawMap用以画出点与路径。
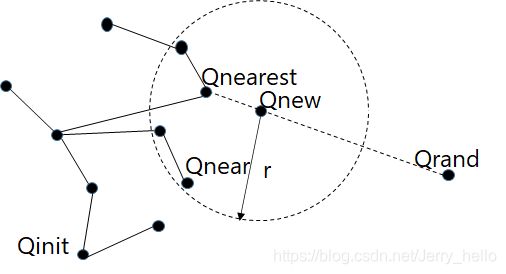
RRT*找Qnew之前的流程与RTT相同,找到Qnew,判断其有效性后。不直接连接Qnew与Qnearest,而是运行函数nearToNew,寻找在指定范围r内的所有节点,遍历所有得到的节点Qnear,判断Qnear中到Qnew与Qnear到Qinit代价和最小的节点,指定其为Qnew的父节点连接两点连线。
再执行函数rewire,遍历剩下的节点Qnear,判断如果以Qnew为父节点,其代价是否会小于原来的代价,若小于,则更改其父节点为Qnew。
其中nearToNew用来寻找距离给定点一定范围内的各个节点返回为一个list;
# 获取指定点周围一定范围内的节点
def nearToNew(self, new):
nearTonew = []
nearCost = []
for item in self.tree:
costToNew = self.cost(item.loc, new)
if costToNew < self.step * 2:
# 判断两点之间的连线是否穿过障碍物
if self.is_block(item.loc, new):
continue
nearTonew.append(item)
nearCost.append(int(costToNew) + int(item.cost))
return nearTonew,nearCost
函数rewire用来重新规划Qnew周围的路径:
# 重新规划新节点new与其周围节点之间的路径
def rewire(self, nearTonew, newPoint):
for item2 in nearTonew:
costToNew = self.cost(item2.loc, newPoint.loc)
if costToNew + newPoint.cost < item2.cost:
# 判断两点之间路线是否穿过障碍物
if self.is_block(item2.loc, newPoint.loc):
continue
cv2.line(self.map.drawMap, tuple(item2.loc), tuple(item2.fatherPoint.loc), (255, 255, 255))
item2.fatherPoint = newPoint
item2.cost = costToNew + newPoint.cost
cv2.line(self.map.drawMap, tuple(item2.loc), tuple(item2.fatherPoint.loc), (0, 255, 0))
cv2.imshow("route", self.map.drawMap)
cv2.waitKey(self.speed)
以上代码都是我在整个RRT*代码中截取出来的片段,仅供参考大致思路。
以下是RRT*完整代码,初写代码,可能不太标准,仅供参考,也算是对于自己学习的记录。
# -*- coding = utf-8 -*-
# @Time : 2021/4/14 9:07
import random
import cv2
import math
import copy
import time
from numpy import mean
class Point(object):
def __init__(self,loc, cost, fatherPoint = None):
self.loc = loc
self.cost = cost
self.fatherPoint = fatherPoint
class Map(object):
point = []
def __init__(self, img):
self.drawMap = cv2.imread(img)
self.checkMaps = cv2.imread(img, cv2.IMREAD_GRAYSCALE)
self.width = self.checkMaps.shape[1]
self.height = self.checkMaps.shape[0]
def on_EVENT_LBUTTONDOWN(self,event, x, y, flags, param):
# point = []
if event == cv2.EVENT_LBUTTONDOWN:
xy = '%d,%d' % (x, y)
# global point
self.point.append([x,y])
# print('x, y = {}, {}'.format(x, y))
cv2.circle(self.drawMap, (x, y), 1, (255, 0, 0), thickness=-1)
cv2.putText(self.drawMap, xy, (x, y), cv2.FONT_HERSHEY_PLAIN,1.0, (0, 0, 0), thickness=1)
cv2.imshow('image', self.drawMap)
def start_end(self):
cv2.namedWindow('image')
cv2.imshow('image', self.checkMaps)
cv2.setMouseCallback('image', self.on_EVENT_LBUTTONDOWN)
cv2.waitKey(0)
cv2.destroyAllWindows()
print("起点:", self.point[0], "终点:", self.point[1])
return self.point
def is_block(self,a):
if self.checkMaps[a[1], a[0]] == 0:
return True
else:
return False
def Route(self,point,v):
a = point.loc
b = point.fatherPoint.loc
cv2.line(self.drawMap,tuple(a),tuple(b),(0,0,255),3)
cv2.imshow('route', self.drawMap)
cv2.waitKey(v)
return point.fatherPoint
class RRTStar(object):
tree = []
def __init__(self,map,step,speed = 10):
self.step = step
self.map = map
self.speed = speed
return
# 获得随机点Q的坐标
def Sample(self, a, b):
Q = [random.randint(0, a), random.randint(0, b)]
return Q
# 计算两点之间的代价
def cost(self, a, b):
c = math.sqrt((a[0] - b[0])**2 + (a[1] - b[1])**2)
return c
# 找到离随机点Q最近的节点
def nearest(self, q, tree):
a = []
for item in tree:
a.append(self.cost(q, item.loc))
b = tree[a.index(min(a))]
return b
# 获取Q与最近节点之间的拓展点
def extend(self, a, b, c = 10):
d = [0, 0]
d[0] = a[0] + int(c * (b[0] - a[0]) / math.sqrt((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2))
d[1] = a[1] + int(c * (b[1] - a[1]) / math.sqrt((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2))
return d
# 取得指定点之间的的碰撞监测点
def checkPoint(self, point1, point2):
a = copy.deepcopy(point1)
b = copy.deepcopy(point2)
if a[0] > b[0]:
a[0],b[0] = b[0],a[0]
a[1],b[1] = b[1],a[1]
q = 3
c = []
if a[0] == b[0]:
if a[1] > b[1]:
a[1],b[1] = b[1],a[1]
for i in range(a[1] - q, b[1] + q):
c.append([a[0], i])
c.append([a[0] - q, i])
c.append([a[0] + q, i])
else:
for i in range(a[0] - q,b[0] + q):
d = (b[1] - a[1])/(b[0] - a[0]) * (i - a[0]) + a[1]
e = (b[1] - a[1])/(b[0] - a[0]) * (i - a[0]) + a[1] + q
f = (b[1] - a[1])/(b[0] - a[0]) * (i - a[0]) + a[1] - q
c.append([i, int(d)])
c.append([i, int(e)])
c.append([i, int(f)])
return c
# 利用梯度下降法生对路径进行平滑处理
def smoothPoint(self,path, weight_data=0.5, weight_smooth=0.5, tolerance=0.00001):
N = len(path)
newpath = copy.deepcopy(path)
err = 2 * tolerance
while err > tolerance:
err = 0.
for i in range(1, N - 1):
for j in range(2):
delta = weight_data * (path[i][j] - newpath[i][j]) + \
weight_smooth * (newpath[(i - 1) % N][j] + newpath[(i + 1) % N][j] - 2.0 * newpath[i][j])
newpath[i][j] += delta
err += abs(delta)
return newpath
# 碰撞检测
def is_block(self, a, b):
for i in self.checkPoint(a, b):
if 0 < i[0] < self.map.width and 0 < i[1] < self.map.height:
if self.map.is_block(i):
return True
else:
return True
return False
# 获取指定点周围一定范围内的节点
def nearToNew(self, new):
nearTonew = []
nearCost = []
for item in self.tree:
costToNew = self.cost(item.loc, new)
if costToNew < self.step * 2:
# 判断两点之间的连线是否穿过障碍物
if self.is_block(item.loc, new):
continue
nearTonew.append(item)
nearCost.append(int(costToNew) + int(item.cost))
return nearTonew,nearCost
# 重新规划新节点new与其周围节点之间的路径
def rewire(self, nearTonew, newPoint):
for item2 in nearTonew:
costToNew = self.cost(item2.loc, newPoint.loc)
if costToNew + newPoint.cost < item2.cost:
# 判断两点之间路线是否穿过障碍物
if self.is_block(item2.loc, newPoint.loc):
continue
cv2.line(self.map.drawMap, tuple(item2.loc), tuple(item2.fatherPoint.loc), (255, 255, 255))
item2.fatherPoint = newPoint
item2.cost = costToNew + newPoint.cost
cv2.line(self.map.drawMap, tuple(item2.loc), tuple(item2.fatherPoint.loc), (0, 255, 0))
cv2.imshow("route", self.map.drawMap)
cv2.waitKey(self.speed)
# 在图上画出路径
def drawRoute(self, point):
routePoint = []
c = point
routePoint.append(point.loc)
while True:
c = self.map.Route(c, self.speed)
routePoint.append(c.loc)
if c.loc == start:
break
return routePoint
# 在图上画出平滑处理后的路径
def Smooth(self, routePoint):
s = self.smoothPoint(routePoint)
for i in range(len(s)):
if i == len(s) - 1:
break
x = (int(s[i][0]), int(s[i][1]))
y = (int(s[i + 1][0]), int(s[i + 1][1]))
cv2.line(self.map.drawMap, x, y, (0, 0, 255), 2)
cv2.imshow("route", self.map.drawMap)
cv2.waitKey(self.speed)
cv2.imshow("route", self.map.drawMap)
cv2.waitKey(0)
def Path(self, start, end):
speed = self.speed
tree = self.tree
tree.append(Point(start,0))
t = 0
while t < 2000:
tag = 0
# 取得随机点q
q = self.Sample(self.map.width, self.map.height)
# 取得离随机点最近的点
nearest = self.nearest(q, tree)
if q == nearest.loc:
continue
# 获得拓展点new
new = self.extend(nearest.loc, q, self.step)
# 获得在拓展点两个步长范围内的所有点,取得其中到拓展点代价最小的点,作为拓展点父节点
nearTonew,nearCost = self.nearToNew(new)
#如果拓展点附近没有复合要求的点,则结束此次循环,重新选择拓展点
if nearCost:
pass
else:
continue
minCostPoint = nearTonew[nearCost.index(min(nearCost))]
nearTonew.remove(minCostPoint)
newPoint = Point(new, min(nearCost), minCostPoint)
t += 1
# 标出拓展点位置,画出拓展点与其父节点之间的线
cv2.circle(self.map.drawMap, tuple(new), 2, (255, 0, 0), thickness=-1)
cv2.line(self.map.drawMap, tuple(newPoint.loc), tuple(newPoint.fatherPoint.loc), (0, 255, 0))
tree.append(newPoint)
cv2.imshow("route", self.map.drawMap)
cv2.waitKey(speed)
# 浏览拓展点周围的其他点,判断以拓展点为父节点的代价与原本的代价的大小,若小于原本的代价,则将拓展点改为其父节点
self.rewire(nearTonew, newPoint)
# 判断是否到达终点,画出路径,并进行平滑处理
if abs(new[0] - end[0]) < 20 and abs(new[1] - end[1]) < 20:
tag = 1
routePoint = self.drawRoute(newPoint)
# self.Smooth(routePoint)
break
if tag == 1:
print("RRT*寻路成功")
else:
print("RRT*寻路失败")
if __name__ == "__main__":
t0 = 0
T = []
while t0 < 10:
map = Map("../work/testmap.png")
time1 = time.time()
start = [50, 50]
end = [800, 400]
cv2.circle(map.drawMap, (start[0], start[1]), 2, (255, 0, 0), thickness=-1)
cv2.rectangle(map.drawMap, (end[0] - 20, end[1] - 20), (end[0] + 20, end[1] + 20), (255, 0, 0))
a = RRTStar(map, 30, 1)
print(len(a.tree))
a.Path(start, end)
a.tree.clear()
time2 = time.time()
T.append(time2 - time1)
t0 += 1
cv2.destroyAllWindows()
print(mean(T))
print(T)
