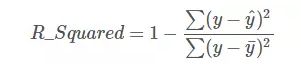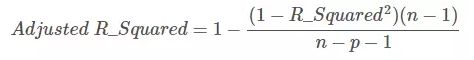机器学习常见笔试题
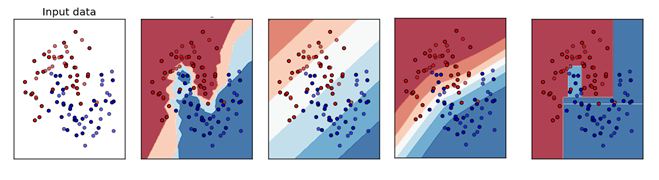
Q1. 下面哪个对应的是正确的 KNN 决策边界?
A. A
B. B
C. C
D. D
答案:A
解析:本题考查的是 KNN 的相关知识点。
KNN 分类算法是一个比较成熟也是最简单的机器学习(Machine Learning)算法之一。该方法的思路是:如果一个样本在特征空间中与K个实例最为相似(即特征空间中最邻近),那么这 K 个实例中大多数属于哪个类别,则该样本也属于这个类别。其中,计算样本与其他实例的相似性一般采用距离衡量法。离得越近越相似,离得越远越不相似。因此,决策边界可能不是线性的。
Q2. 如果一个经过训练的机器学习模型在测试集上达到 100% 的准确率,这是否意味着该模型将在另外一个新的测试集上也能得到 100% 的准确率呢?
A. 是的,因为这个模型泛化能力已经很好了,可以应用于任何数据
B. 不行,因为还有一些模型不确定的东西,例如噪声
答案:B
解析:本题考查的是机器学习泛化能力与噪声。
现实世界的数据并不总是无噪声的,所以在这种情况下,我们不会得到 100% 的准确度。
Q3. 下面是交叉验证的几种方法:
1. Bootstrap
2. 留一法交叉验证
3. 5 折交叉验证
4. 重复使用两次 5 折交叉验证
请对上面四种方法的执行时间进行排序,样本数量为 1000。
A. 1 > 2 > 3 > 4
B. 2 > 3 > 4 > 1
C. 4 > 1 > 2 >3
D. 2 > 4 > 3 > 1
答案:D
解析:本题考查的是 k 折交叉验证和 Bootstrap 的基本概念。
Bootstrap 是统计学的一个工具,思想就是从已有数据集 D 中模拟出其他类似的样本 Dt。Bootstrap 的做法是,假设有 N 笔资料,先从中选出一个样本,再放回去,再选择一个样本,再放回去,共重复 N 次。这样我们就得到了一个新的 N 笔资料,这个新的 Dt 中可能包含原 D 里的重复样本点,也可能没有原 D 里的某些样本,Dt 与 D 类似但又不完全相同。值得一提的是,抽取-放回的操作不一定非要是 N,次数可以任意设定。例如原始样本有 10000 个,我们可以抽取-放回 3000 次,得到包含 3000 个样本的 Dt 也是完全可以的。因此,使用 bootstrap 只相当于有 1 个模型需要训练,所需时间最少。
留一法(Leave-One-Out)交叉验证每次选取 N-1 个样本作为训练集,另外一个样本作为验证集,重复 N 次。因此,留一法相当于有 N 个模型需要训练,所需的时间最长。
5 折交叉验证把 N 个样本分成 5 份,其中 4 份作为训练集,另外 1 份作为验证集,重复 5 次。因此,5 折交叉验证相当于有 5 个模型需要训练。
2 次重复的 5 折交叉验证相当于有 10 个模型需要训练。
Q4. 变量选择是用来选择最好的判别器子集, 如果要考虑模型效率,我们应该做哪些变量选择的考虑?(多选)
A. 多个变量是否有相同的功能
B. 模型是否具有解释性
C. 特征是否携带有效信息
D. 交叉验证
答案:ACD
解析:本题考查的是模型特征选择。
如果多个变量试图做相同的工作,那么可能存在多重共线性,影响模型性能,需要考虑。如果特征是携带有效信息的,总是会增加模型的有效信息。我们需要应用交叉验证来检查模型的通用性。关于模型性能,我们不需要看到模型的可解释性。
Q6. 如果在线性回归模型中额外增加一个变量特征之后,下列说法正确的是?
A. R-Squared 和 Adjusted R-Squared 都会增大
B. R-Squared 保持不变 Adjusted R-Squared 增加
C. R-Squared 和 Adjusted R-Squared 都会减小
D. 以上说法都不对
答案:D
解析:本题考查的是线性回归模型的评估准则 R-Squared 和 Adjusted R-Squared。
线性回归问题中,R-Squared 是用来衡量回归方程与真实样本输出之间的相似程度。其表达式如下所示:
上式中,分子部分表示真实值与预测值的平方差之和,类似于均方差 MSE;分母部分表示真实值与均值的平方差之和,类似于方差 Var。根据 R-Squared 的取值,来判断模型的好坏:如果结果是 0,说明模型拟合效果很差;如果结果是 1,说明模型无错误。一般来说,R-Squared 越大,表示模型拟合效果越好。R-Squared 反映的是大概有多准,因为,随着样本数量的增加,R-Square必然增加,无法真正定量说明准确程度,只能大概定量。
单独看 R-Squared,并不能推断出增加的特征是否有意义。通常来说,增加一个特征,R-Squared 可能变大也可能保持不变,两者不一定呈正相关。
如果使用校正决定系数(Adjusted R-Square):
其中,n 是样本数量,p 是特征数量。Adjusted R-Square 抵消样本数量对 R-Square的影响,做到了真正的 0~1,越大越好。若增加的特征有效,则 Adjusted R-Square 就会增大,反之则减小。
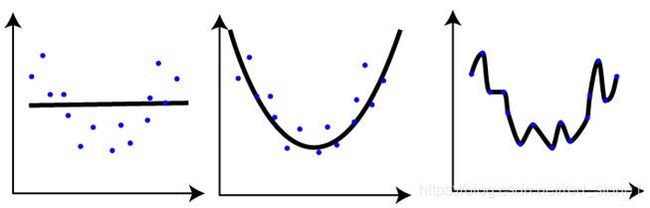
Q7. 如下图所示,对同一数据集进行训练,得到 3 个模型。对于这 3 个模型的评估,下列说法正确的是?(多选)
A. 第一个模型的训练误差最大
B. 第三个模型性能最好,因为其训练误差最小
C. 第二个模型最稳健,其在测试集上表现应该最好
D. 第三个模型过拟合
答案:ACD
解析:本题考查的是机器学习模型欠拟合、过拟合概念。
很简单,第一个模型过于简单,发生欠拟合,训练误差很大,在训练样本和测试样本上表现都不佳。第二个模型较好,泛化能力强,模型较为健壮,在训练样本和测试样本上表现都不错。第三个模型过于复杂,发生过拟合,训练样本误差虽然很小,但是在测试样本集上一般表现很差,泛化能力很差。
模型选择应该避免欠拟合和过拟合,对于模型复杂的情况可以选择使用正则化方法。
Q8. 如果使用线性回归模型,下列说法正确的是?
A. 检查异常值是很重要的,因为线性回归对离群效应很敏感
B. 线性回归分析要求所有变量特征都必须具有正态分布
C. 线性回归假设数据中基本没有多重共线性
D. 以上说法都不对
答案:A
解析:本题考查的是线性回归的一些基本原理。
异常值是数据中的一个非常有影响的点,它可以改变最终回归线的斜率。因此,去除或处理异常值在回归分析中一直是很重要的。
了解变量特征的分布是有用的。类似于正态分布的变量特征对提升模型性能很有帮助。例如,数据预处理的时候经常做的一件事就是将数据特征归一化到(0,1)分布。但这也不是必须的。
当模型包含相互关联的多个特征时,会发生多重共线性。因此,线性回归中变量特征应该尽量减少冗余性。C 选择绝对化了。
Q9. 建立线性模型时,我们看变量之间的相关性。在寻找相关矩阵中的相关系数时,如果发现 3 对变量(Var1 和 Var2、Var2 和 Var3、Var3 和 Var1)之间的相关性分别为 -0.98、0.45 和 1.23。我们能从中推断出什么呢?(多选)
A. Var1 和 Var2 具有很高的相关性
B. Var1 和 Var2 存在多重共线性,模型可以去掉其中一个特征
C. Var3 和 Var1 相关系数为 1.23 是不可能的
答案:ABC
解析:本题考查的是相关系数的基本概念。
Var1 和 Var2 之间的相关性非常高,并且是负的,因此我们可以将其视为多重共线性的情况。此外,当数据中存在多重线性特征时,我们可以去掉一个。一般来说,如果相关大于 0.7 或小于 -0.7,那么我们认为特征之间有很高的相关性。第三个选项是不言自明的,相关系数介于 [-1,1] 之间,1.23 明显有误。
Q10. 如果自变量 X 和因变量 Y 之间存在高度的非线性和复杂关系,那么树模型很可能优于经典回归方法。这个说法正确吗?
A. 正确
B. 错误
答案:A
解析:本题考查的是回归模型的选择。
当数据是非线性的时,经典回归模型泛化能力不强,而基于树的模型通常表现更好。
更多原创内容请点击文末的阅读原文查看!
参考文献:
https://www.analyticsvidhya.com/blog/2016/11/solution-for-skilltest-machine-learning-revealed/