感知机对偶算法

知识源于——《统计学习方法（第二版）》李航

感知机（perception)一种二分类的线性分类模型。输入为实例的特征向量，输出为实例的类别（二分类类别为-1，+1二值）。

        用算法2.2（感知机学习算法的对偶形式）代码实现例2.2：

一，实验目的

        用算法2.2（感知机学习算法的对偶形式）完成例2.2：

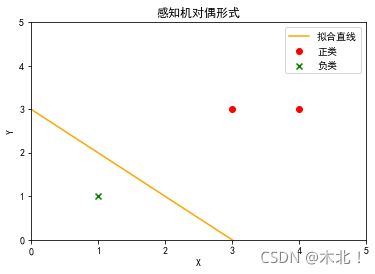
        正样本点是x1=(3,3)T, x2=(4,3)T,负样本点x3=(1,1)T，用感知机学习对偶形式求感知机模型。

二，实验内容

        1.根据拉格朗日对偶性，可将原始算法的极小极大问题转化为对偶算法的极大极小问题。感知机模型：f(x)= sign(w*x+b)，即

         2.最后参考P44算法2.2，实现P45例题，绘制出分类图像。

三，实验步骤与方法

算法过程为：        

        输入：线性可分的数据集T={x1,y1,x2,y2,…(xn,yn)},其中xi∈Rn,yi∈{-1,+1}，i=1,2,…N;学习率η（0<η≤1）

        输出：α，β；感知机模型    ,其中α={α1,α2,…,αn}T

1. 首先取α1，α2，α3为0，取b=0，学习率为1
2. 计算Gram矩阵    
3. 判断误分类条件 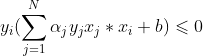   ，为误分类
4. 若误分类，更新参数αi，b
5. 重复第三四步，直到无误分类点，停止迭代，
6. 取得感知机模型的分离超平面，求出感知机模型。

四，代码实现

# -*- coding: utf-8 -*-
"""
Created on Wed Sep 29 01:38:37 2021

@author: lx
"""

import numpy as np
import matplotlib.pyplot as plt
 
def Gram(x_list): 
    ''' 计算Gram矩阵 '''
    G = [[0 for j in range(len(x_list))] for i in range(len(x_list))]
    for i in range(len(x_list)):
        for j in range(i, len(x_list)):
           G[i][j] = x_list[i][0]*x_list[j][0] + x_list[i][1]*x_list[j][1]
           G[j][i] = G[i][j]
    return G
 
def Perceptron_Study_antithesis(x_list, y_list):
    alpha = np.zeros(len(y_list))
    b = 0
    rate = 1 # 学习率
    item = 0 # 迭代次数
    G = Gram(x_list) # 计算Gram矩阵
    while True:
        flag = 0
        for i in range(len(y_list)):
            temp = 0
            for j in range(len(y_list)):
                temp += alpha[j]*y_list[j]*G[j][i]
            
            if y_list[i]*(temp + b) > 0:
                flag += 1
                continue
            else:
                item += 1
                alpha[i] += rate
                b += y_list[i]*rate
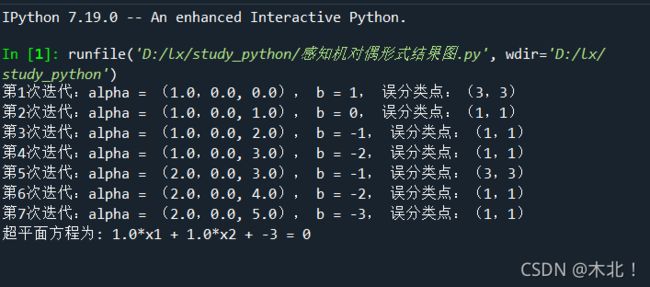
                print('第{}次迭代：alpha = （{}，{}, {}）， b = {}， 误分类点：（{}，{}）'.format(item, alpha[0], alpha[1], alpha[2], b, x_list[i][0], x_list[i][1]))
                break
        if flag == len(y_list): # 全部分对，不再调整方程
            w = [0, 0]
            for i in range(len(y_list)):
                w[0] += alpha[i]*y_list[i]*x_list[i][0]
                w[1] += alpha[i]*y_list[i]*x_list[i][1]
            print('超平面方程为: {}*x1 + {}*x2 + {} = 0'.format(w[0], w[1], b))
            plt.rcParams['font.sans-serif']=['SimHei']
            plt.rcParams['axes.unicode_minus'] = False
            plt.xlabel('X')
            plt.ylabel('Y')
            plt.xlim(xmax=5,xmin=0)
            plt.ylim(ymax=5,ymin=0)
            
            x1=np.array([3,4])
            y1=np.array([3,3])
            
            x3 = np.array([1])
            y3 = np.array([1])
             
            plt.scatter(x1, y1, marker = 'o', alpha=1,color="red", label='正类')
            plt.scatter(x3, y3, marker = 'x', alpha=1,color="green", label='负类')
            
            x2 = np.arange(0,5,0.1)
            y2 = -((w[0])*x2 +b)/(w[1]+0.000001)
            
            plt.plot(x2,y2,label="拟合直线",c='orange')
             
            plt.legend()
            plt.title('感知机对偶形式')#图的标题
            plt.show()
            break
        
if __name__ == '__main__':
    x_list = [(3,3), (4,3), (1,1)]
    y_list = [1, 1, -1]
    Perceptron_Study_antithesis(x_list, y_list)
    
            

五，实验结果

 

 欢迎大佬指点交流。感谢浏览。学习的文章：

1.  感知机理论知识（知识点相同，但用c写的代码）：感知机的原始形式和对偶形式在解决问题的计算上是一致的，但是他们的思想不同，原始形式的基本思想是对于误分类点，调整w和b，使分类超平面向该误分类点的一侧移动，以减少该误分类点与超平面的距离，直到超平面越过该误分类点使其被正确分类为止。 而对偶形式的基本思想是将w和b表示成x和y的线性组合形式，从而求出w和b。 
   《李航：统计学习方法》笔记之感知机_龙在天涯-CSDN博客
2. 感知机python代码实现《李航统计学习方法》第二章：感知机学习算法 - 算法代码_potato_cyy的博客-CSDN博客
3. 另一种实现感知机思路统计学习方法第2章 感知机 Python实现_sinat_41758351的博客-CSDN博客