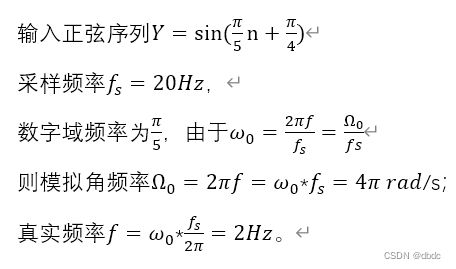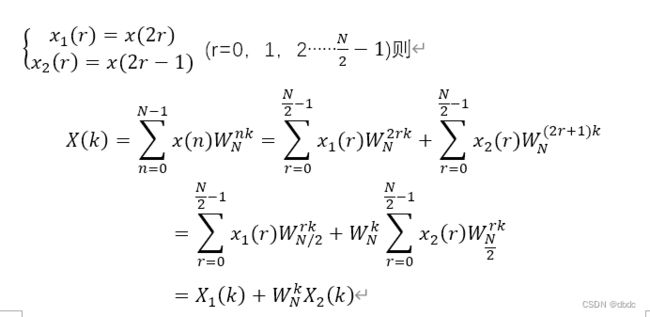基于matlab环境下的自定义fft函数实现

名称：

基于matlab环境下的fft函数实现

目的：

初步掌握matlab编程，实现fft函数，掌握数字信号处理中各种频率的基本关系，掌握窗函数的使用及其原理。

过程：

FFT是通过蝶形运算实现快速计算DFT的函数。

程序流程：

一：实现序列的倒序

1：输入序列X;

2：计算序列的长度；

3：求出序列长度的对数；

4：设置中介序列Y;

5：设置模拟值K进行比较运算实现序列X倒序并存储到序列Y中。

二：进行蝶形运算

    主要计算旋转因子和蝶形运算等级

三：结果输出

数据：

一：频率不同的正弦序列输入：

Y=sin(（π/5）n+π/4)

取采样频率fs=1000Hz ;采样点数N为1024;则采样分辨率∆f=fs/N  ;时间序列t=n/fs ；（其中n为1-1024的整数序列），真实频率f=100Hz

输出数据：

 

图3

Y=sinπ（（π/5）n+π/4）

取采样频率fs=1000Hz ;采样点数N为512;真实频率f=100Hz 输出数据：

 

图4

Y=sin(（3π/10）n+π/4)

取采样频率fs=1000Hz ;采样点数N为1024;真实频率f=150Hz

输出数据：

 

图5

Y=sin(（39π/100）n+π/4)

取采样频率fs=1000Hz ;采样点数N为1024;真实频率f=195Hz

输出数据：

 

图6

Y=sin(（3π/5）n+π/4)

取采样频率fs=1000Hz ;采样点数N为1024;真实频率f=300Hz

输出数据：

 

图7

Y=sin(（233π/250）n+π/4)

取采样频率fs=1000Hz ;采样点数N为1024;真实频率f=466Hz

输出数据：

 

图8

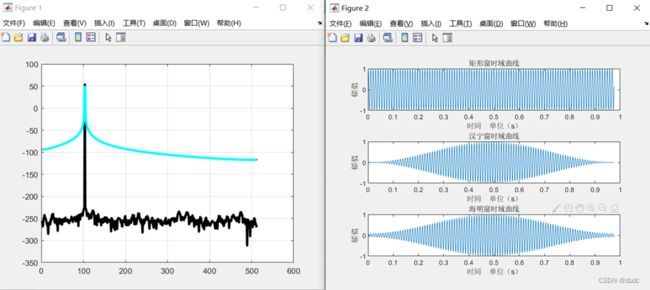
与随机序列相同，将两组输出数据放置同一图像中，易见两数据相同。

三.同频率信号在不同窗函数下在的区别

Y=sin（（π/5）n+π/4）

黑：矩形窗

红：汉宁窗

蓝：海明窗

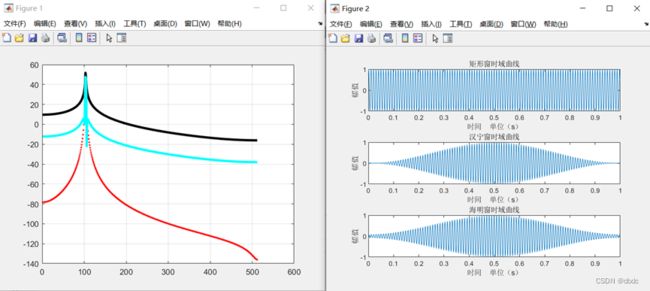
当窗函数取整周期时：

取采样频率fs=1000Hz ;采样点数N为1000。

 

图9

矩形窗后的信号能量值：Ex1 =500.0000     

汉宁窗后的信号能量值：Ex2 =187.3125

海明窗后的信号能量值：Ex3 =198.5045

当窗函数取非整周期时：

取采样频率fs=1000Hz ;采样点数N为1024。

 

图10

矩形窗后的信号能量值：Ex1 =512.4755

汉宁窗后的信号能量值：Ex2 =191.8125

海明窗后的信号能量值：Ex3 =203.2763

讨论与分析

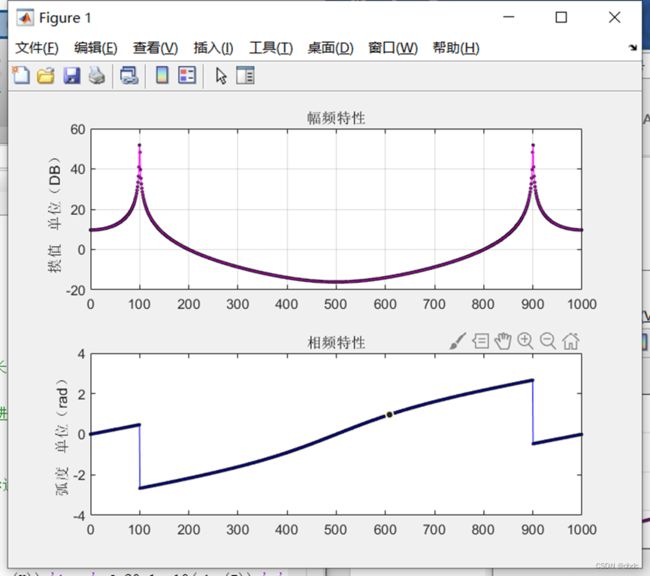
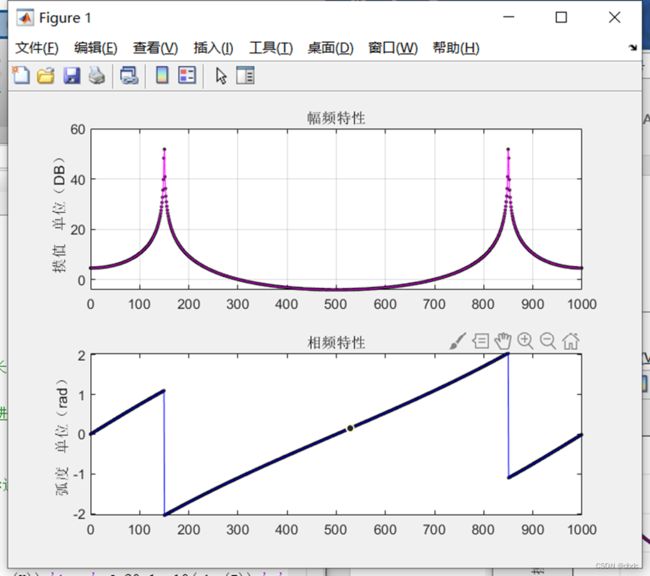
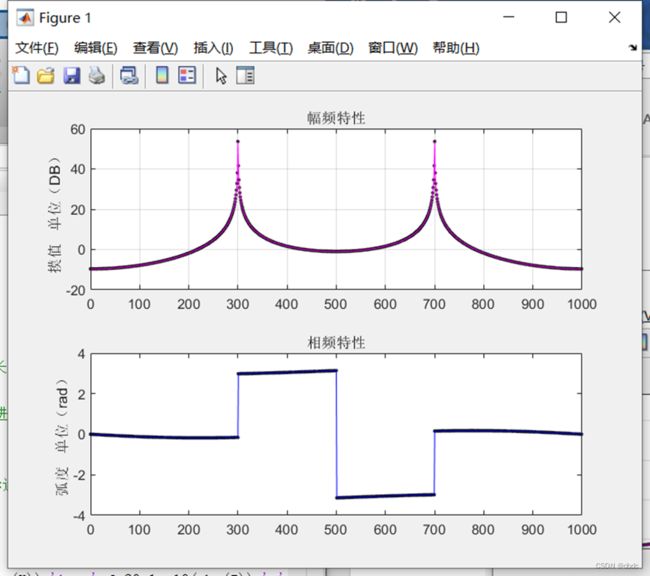
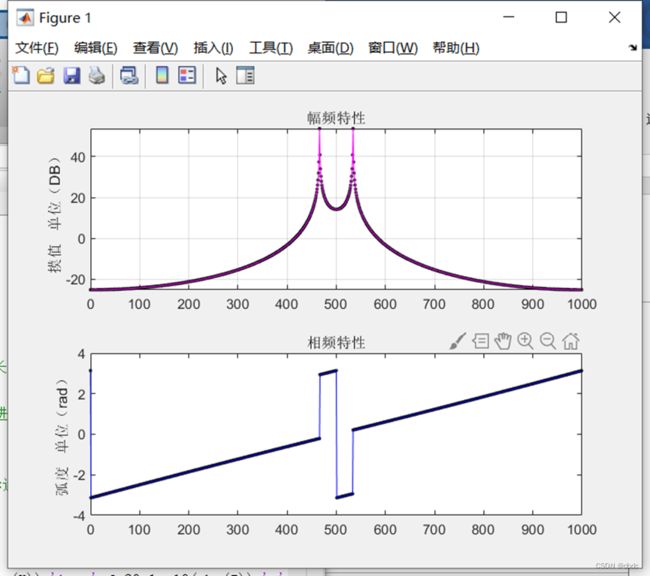
fft后频域图，幅频关于fs/2偶对称，相频关于fs/2奇对称，因此画频域图时支取采样分辨率的一半即可。

FFT、DFT的计算量比较：

直接DFT计算复数加法次数为N*(N-1);复数乘法次数为N*N；

而DIT_FFT计算复数加法次数为 ;复数乘法次数为N*log2N 。

（在matlab中只有序列的长度 时，傅里叶变换采用FFT，若长度不满足条件则采用DFT，所以取样时保证采样点个数等于 可提高运算速度）

正弦函数数字域频率、真实频率、采样率之间的关系：

 

 

窗的影响：

对于截取后的序列仍为周期序列，理论上则不会产生截断效应即采用矩形窗误差更小；对于截取后的序列不为周期序列，采用合理的窗函数后可有效减少截断效应;

加窗后会使信号的幅值失真即能量变小;

主瓣越窄的窗函数的频率识别精度越高；旁瓣衰减越大的窗函数的幅度识别精度越高。

海明窗与汉宁窗相比，能量更集中于主瓣

倒位序：将数n的二进制码的位序颠倒后的数。

倒位序的实现方法：0的倒位序为0，所以我们从第一个数开始逐步求出序列的所有倒位序，将该位数的二进制数与其最高位相比较（也就是N/2的二进制数，N为序列的长度），若小于最高位，下一个数则等于该数的最高位加1；若不小于最高位，则先将该数的最高位减1，再将结果数与次高位相比较……其中N/2为特殊序列，这时可将其直接等于1。

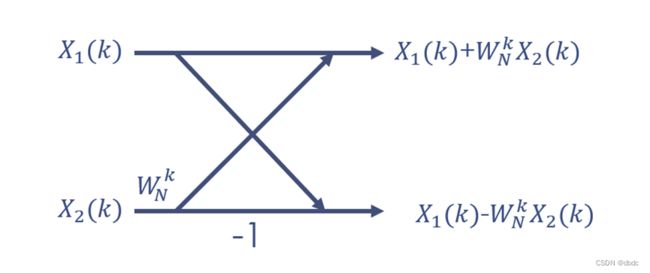
蝶形运算：

设序列x(n) 的序列长度为N，对其进行DFT则（k=0，1，2……N-1;）,若将N非为奇数序列与偶数序列

 

 

可得x(n)的前半部分的DFT变换，复数乘法计算量为 与直接DFT相比计算量减少了一半，后半部分为

 

由于后半部分与前半部分的区别只存在于旋转因子的正负，所有后半部分的复数乘法计算量可忽略不计。

 

最小蝶形运算单元。

上述为将序列按奇偶分为了2部分，若再将x1(r) 和x2(r) 再分为两部分，计算量将再次减少，如此不断的分解直到剩下最后的2点DFT，       FFT完成。

旋转因子的确定：

旋转因子：

 

其中L为当前蝶形运算的级数；M为序列长度的对数；J=0,1,2…（2L-1-1） ；N为序列的长度。