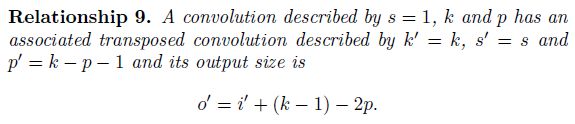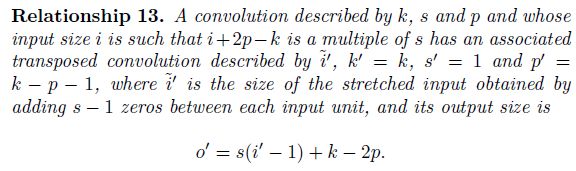深度学习入门 (九):卷积层和池化层的实现
目录
- 卷积神经网络 CNN 整体结构
- 卷积层
-
- 全连接层存在的问题
- 卷积运算
-
- 乘积累加运算
- 偏置
- 填充 (padding)
- 步幅 (stride)
- 小结:卷积层的输出特征图的大小
- 3 维数据的卷积运算
- 结合方块思考卷积运算
- 卷积运算的批处理
- 1 × 1 1\times 1 1×1 卷积层
-
- 与全连接层的相似性
- 减小通道数 (bottleneck layer)
- 池化层
-
- Max 池化
- 全局平均池化层 (Global Average Pooling, GAP)
- 池化层的特征
- 卷积层和池化层的实现
-
- 基于 `im2col` 的展开
- 卷积层的实现
-
- 正向传播
- 反向传播
- 代码实现
- Max 池化层的实现
-
- 正向传播
- 反向传播
- 代码实现
- 空洞卷积 (Dilated Convolution)
-
- 空洞卷积
- Hybrid Dilated Convolution (HDC)
- Deformable Convolution (可变形卷积)
-
- Deformable Convolution
- Deformable RoI Pooling (Deformable-RFCN)
- Octave Convolution (降频卷积)
- Transposed convolution (转置卷积)
-
- Convolution as a matrix operation
- Transposed convolution
- No zero padding, unit strides, transposed
- Zero padding, unit strides, transposed
-
- Half (same) padding, transposed
- Full padding, transposed
- No zero padding, non-unit strides, transposed
- Zero padding, non-unit strides, transposed
- 1D Conv
- 参考文献
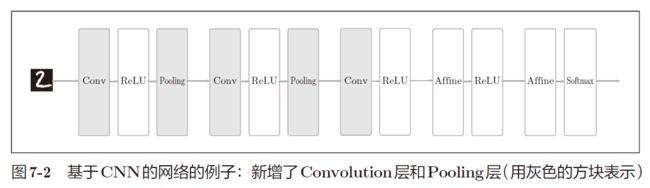
卷积神经网络 CNN 整体结构
CNN: Convolutional Neural Network
- CNN 层的连接顺序是“Convolution - ReLU - (Pooling)”(Pooling 层有时会被省略)。还需要注意的是,在上面的 CNN 中,靠近输出的层中使用了之前的“Affine - ReLU”组合。此外,最后的输出层中使用了之前的“Affine - Softmax”组合。这些都是一般的 CNN 中比较常见的结构
- 卷积层负责进行特征提取,池化层负责降采样:保留显著特征、降低特征维度的同时增大感受野。最后的全连接层负责对特征图进行降维后进行激活分类
- 最后的全连接层参数多,易造成过拟合。因此在很多场景中,可以使用全局平均池化层 (Global Average Pooling, GAP) 来取代最后的全连接层进行降维。因为 GAP 是利用池化实现降维,因此减少了参数量,防止过拟合;同时可以实现任意图像尺度的输入
卷积层
- 将卷积层的输入输出数据称为特征图(feature map)。其中,卷积层的输入数据称为输入特征图(input feature map),输出数据称为输出特征图(output feature map)
全连接层存在的问题
- 数据的形状被“忽视”了。比如,输入数据是图像时,图像通常是高、长、通道方向上的3维形状。但是,向全连接层输入时,需要将3维数据拉平为1维数据。图像是3维形状,这个形状中应该含有重要的空间信息。比如,空间上邻近的像素为相似的值、RBG的各个通道之间分别有密切的关联性、相距较远的像素之间没有什么关联等,3维形状中可能隐藏有值得提取的本质模式。但是,因为全连接层会忽视形状,将全部的输入数据作为相同的神经元(同一维度的神经元)处理,所以无法利用与形状相关的信息
- 在输入输出的数据形状相同的情况下,全连接层所需要训练的参数远远多于卷积层
- 例如,输入为 32 × 32 × 3 32\times 32\times 3 32×32×3, 输出为 28 × 28 × 6 28\times 28\times 6 28×28×6,如果使用全连接层,则需要 32 × 32 × 3 × 28 × 28 × 6 ≈ 14 m ( m i l l i o n ) 32\times 32\times 3 \times 28\times 28\times 6 \approx 14m(million) 32×32×3×28×28×6≈14m(million) 个参数,而如果使用卷积层 (6 个 5 × 5 5 \times 5 5×5 的滤波器)则只需要 150 个参数,加上偏置也只需要 156 个参数
总结:
- 相比于全连接层,卷积层可以用较少的参数提取有效特征
- Parameter sharing: A feature detector (such as a vertical edge detector) that’s useful in one part of the image is probably useful in another part of the image.
卷积运算
乘积累加运算
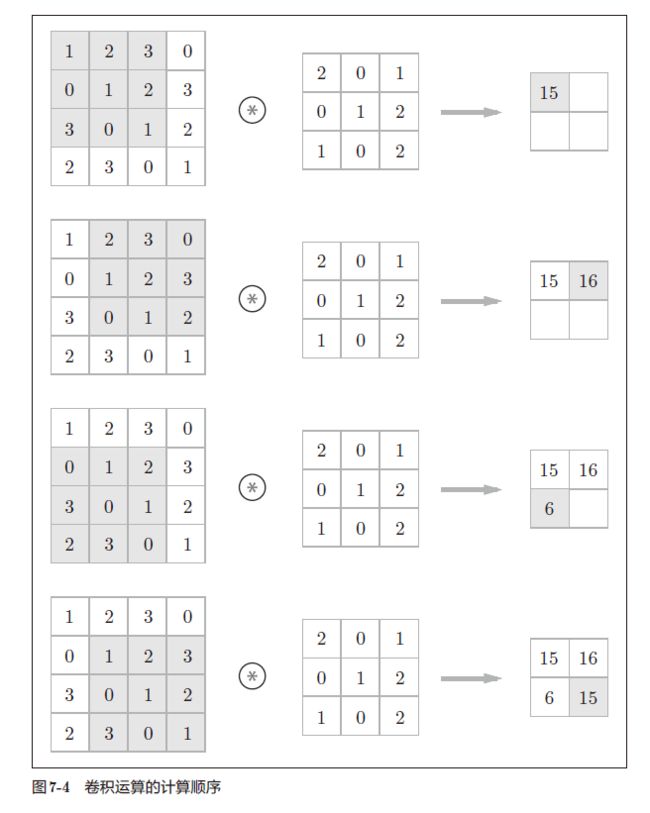
- 对于输入数据,卷积运算以一定间隔滑动滤波器的窗口并应用。如下图所示,将各个位置上滤波器的元素和输入的对应元素相乘,然后再求和,将这个结果保存到输出的对应位置。把这个过程在所有位置都进行一遍,就可以得到卷积运算的输出
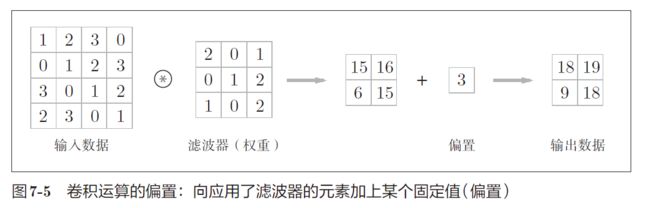
偏置
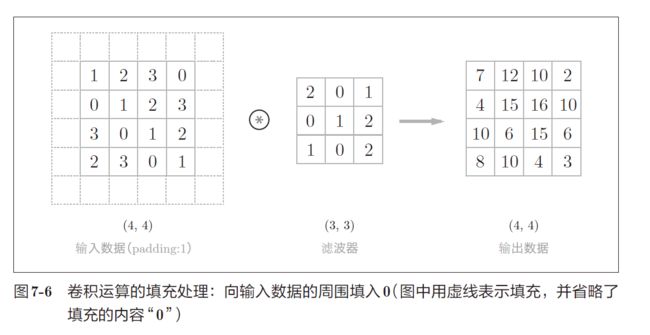
填充 (padding)
- 使用填充主要是为了调整输出的大小
- 比如,对大小为 ( 4 , 4 ) (4, 4) (4,4) 的输入数据应用 ( 3 , 3 ) (3, 3) (3,3) 的滤波器时,输出大小变为 ( 2 , 2 ) (2, 2) (2,2),相当于输出大小比输入大小缩小了 2 2 2 个元素。这在反复进行多次卷积运算的深度网络会成为问题。为什么呢?因为如果每次进行卷积运算都会缩小空间,那么在某个时刻输出大小就有可能变为 1,导致无法再应用卷积运算。为了避免出现这样的情况,就要使用填充。在刚才的例子中,将填充的幅度设为 1,那么相对于输入大小 ( 4 , 4 ) (4, 4) (4,4),输出大小也保持为原来的 ( 4 , 4 ) (4, 4) (4,4)。因此,卷积运算就可以在保持空间大小不变的情况下将数据传给下一层
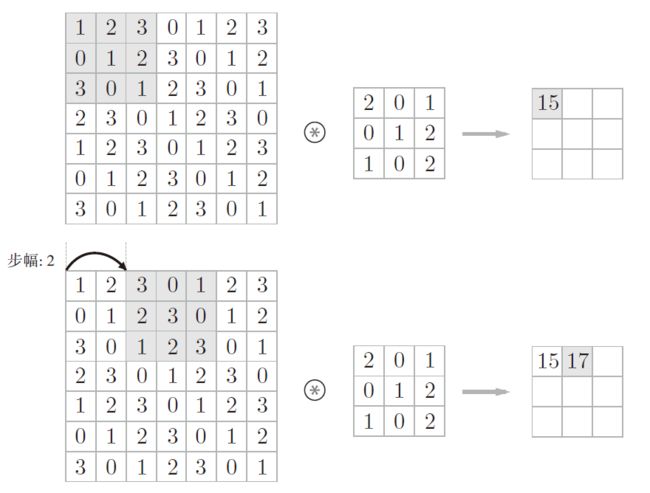
步幅 (stride)
小结:卷积层的输出特征图的大小
- 假设输入大小为 ( H , W ) (H,W) (H,W),滤波器大小为 ( F H , F W ) (FH, FW) (FH,FW),输出大小为 ( O H , O W ) (OH,OW) (OH,OW),填充为 P P P,步幅为 S S S。此时,输出大小为:
O H = H + 2 P − F H S + 1 OH = \frac{H+2P-FH}{S} + 1 OH=SH+2P−FH+1 O W = W + 2 P − F W S + 1 OW = \frac{W+2P-FW}{S} + 1 OW=SW+2P−FW+1 - 设定的卷积核参数必须使上面两式都能除尽,当输出大小无法除尽时(结果是小数时),需要采取报错或四舍五入等对策
- 常用滤波器: 3 × 3 3\times3 3×3 滤波器, P = 1 P=1 P=1, S = 1 S=1 S=1; 这样输出特征图长宽与输入特征图一致
3 维数据的卷积运算
- 图像是 3 维数据,除了高、长方向之外,还需要处理通道方向。通道方向上有多个特征图时,按通道进行输入数据和滤波器的卷积运算,并将结果相加,从而得到输出
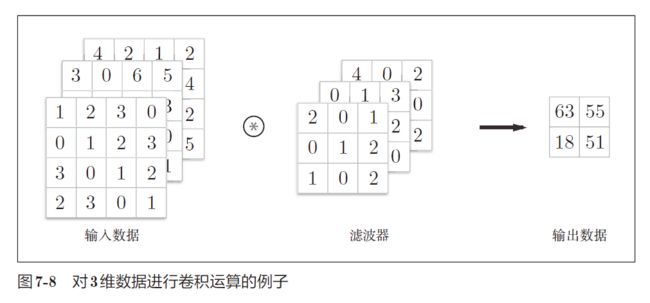 在 3 维数据的卷积运算中,输入数据和滤波器的通道数要设为相同的值。每个通道的滤波器大小要全部相同
在 3 维数据的卷积运算中,输入数据和滤波器的通道数要设为相同的值。每个通道的滤波器大小要全部相同
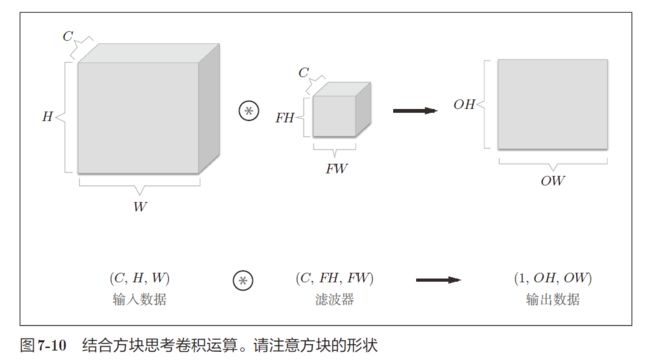
结合方块思考卷积运算
- 如果要在通道方向上也拥有多个卷积运算的输出,就需要用到多个滤波器(权重)
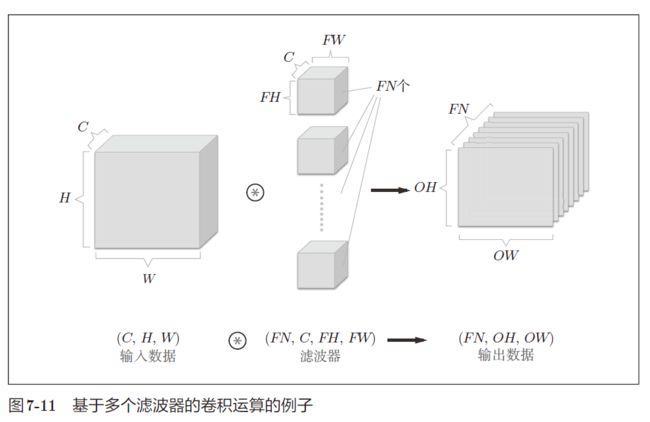
因此,滤波器的形状可以写为 ( o u t p u t _ c h a n n e l , i n p u t _ c h a n n e l , h e i g h t , w i d t h ) (output\_channel, input\_channel, height, width) (output_channel,input_channel,height,width) - 如果再加上偏置运算,则结果如下图所示:
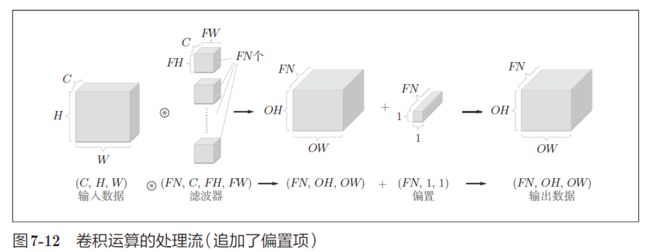
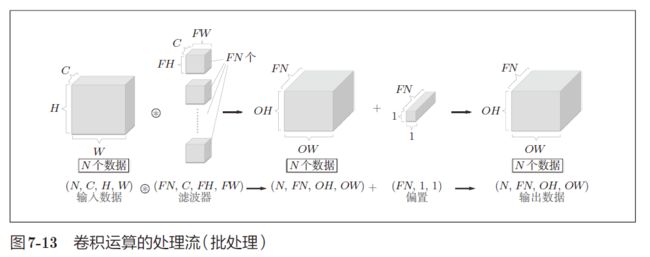
卷积运算的批处理
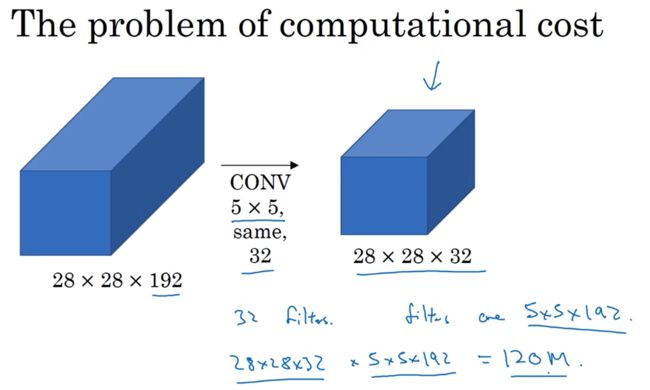
1 × 1 1\times 1 1×1 卷积层
参考: D i v e Dive Dive i n t o into into D e e p Deep Deep L e a r n i n g Learning Learning,吴恩达深度学习视频
与全连接层的相似性
- 1 × 1 1×1 1×1 卷积层即为卷积窗口形状为 1 × 1 1×1 1×1 的多通道卷积层。因为使用了最小窗口, 1 × 1 1×1 1×1 卷积失去了卷积层可以识别高和宽维度上相邻元素构成的模式的功能。实际上, 1 × 1 1×1 1×1 卷积的主要计算发生在通道维上
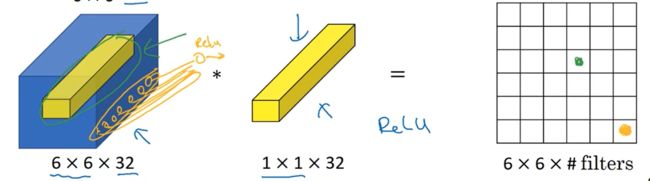 如上图所示,输出中的每个元素来自输入中在高和宽上相同位置的元素在不同通道之间的按权重累加,这就类似于全连接层
如上图所示,输出中的每个元素来自输入中在高和宽上相同位置的元素在不同通道之间的按权重累加,这就类似于全连接层
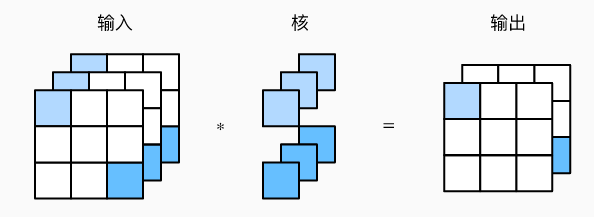 假设我们将通道维当作特征维,将高和宽维度上的元素当成数据样本,那么 1 × 1 1×1 1×1 卷积层的作用与全连接层等价,而且还使空间信息自然地传递到后面的层。即 1 × 1 1×1 1×1 卷积层中可以把通道当作特征,高和宽上的每个元素相当于样本。将输出的通道数设置为类别数之后,再接上后面要讲的全局平均池化层,就可以做到用卷积层代替全连接层了!
假设我们将通道维当作特征维,将高和宽维度上的元素当成数据样本,那么 1 × 1 1×1 1×1 卷积层的作用与全连接层等价,而且还使空间信息自然地传递到后面的层。即 1 × 1 1×1 1×1 卷积层中可以把通道当作特征,高和宽上的每个元素相当于样本。将输出的通道数设置为类别数之后,再接上后面要讲的全局平均池化层,就可以做到用卷积层代替全连接层了!
- 可以这么理解:把每个通道上的二维数据都看作是全连接层上的一个神经元,那么上图就可以看作是一个 3 输入 2 输出的全连接层, ( 2 × 3 ) (2\times3) (2×3) 个卷积核就是全连接层的权重
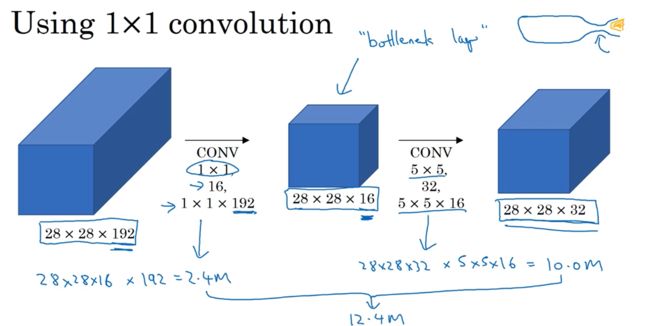
减小通道数 (bottleneck layer)
- 1 × 1 1×1 1×1 卷积层还可以达到减小通道数的作用。虽然其他大小的卷积核在配置适当的 padding 和 srtide 之后也可以在保持宽高不变的情况下减小通道数,但是 1 × 1 1×1 1×1 卷积层所需的乘法运算次数要少一个数量级
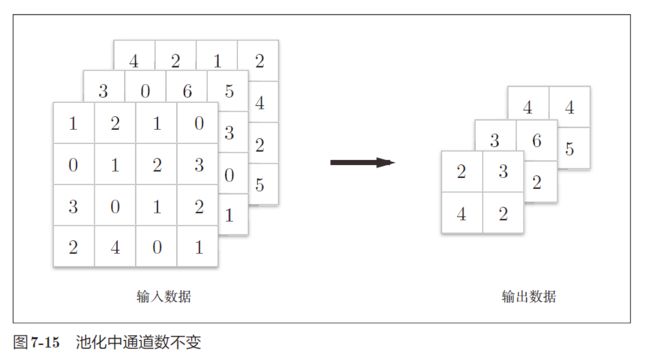
池化层
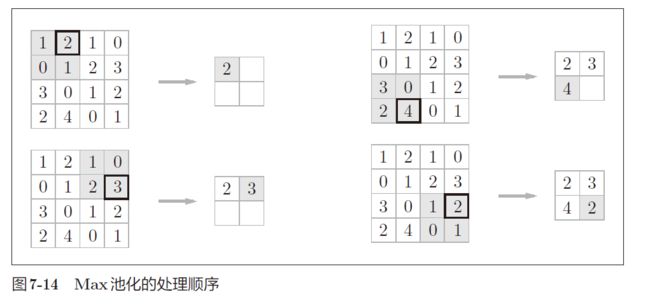
Max 池化
全局平均池化层 (Global Average Pooling, GAP)
参考:https://www.jianshu.com/p/510072fc9c62
- 在常见的卷积神经网络中,全连接层之前的卷积层负责对图像进行特征提取,在获取特征后,传统的方法是接上全连接层之后再进行激活分类,而 GAP 的思路是使用 GAP 来替代该全连接层(即使用池化层的方式来降维) (在 NiN 网络中,它的前面还接了一个 NiN 块,其中使用了 1 × 1 1\times 1 1×1 卷积层), 更重要的一点是保留了前面各个卷积层和池化层提取到的空间/语义信息, 所以在实际应用中效果提升也较为明显。另外, GAP 去除了对输入大小的限制, 而且在卷积可视化 Grad-CAM 中也有重要的应用
- GAP 直接从 feature map 的通道信息下手,比如我们现在的分类有 N N N 种,那么最后一层的卷积输出的 feature map 就只有 N N N 个通道,然后对这个 feature map 进行全局池化操作,获得长度为 N N N 的向量,这就相当于直接赋予了每个通道类别的意义
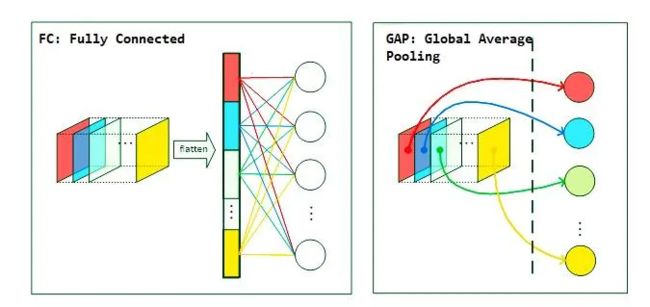
GAP 优点:
- 由于有 GAP,特征图的各个通道可以更直观的被解读为图片属于每个类别的概率
- 利用池化实现了降维,减少了参数量,防止过拟合
- 保留了前面各个卷积层和池化层提取到的空间信息/语义信息,更具有鲁棒性
- 可以实现任意图像尺度的输入
池化层的特征
- 因此,池化层可以降低特征图的参数量,提升计算速度,增加感受野,是一种降采样的操作。可使模型更关注全局特征而非局部出现的位置,提升容错能力,一定程度上防止过拟合
卷积层和池化层的实现
基于 im2col 的展开
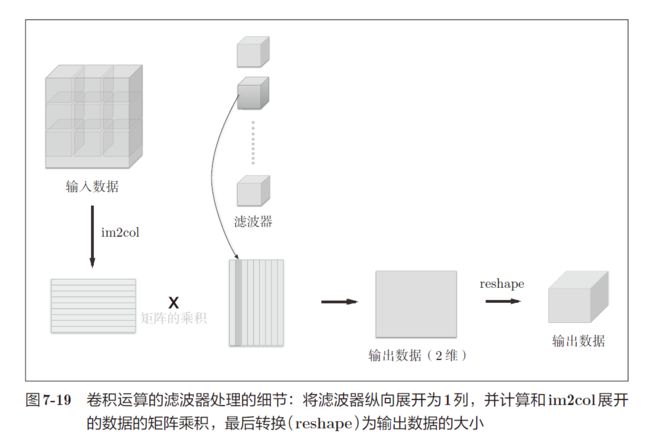
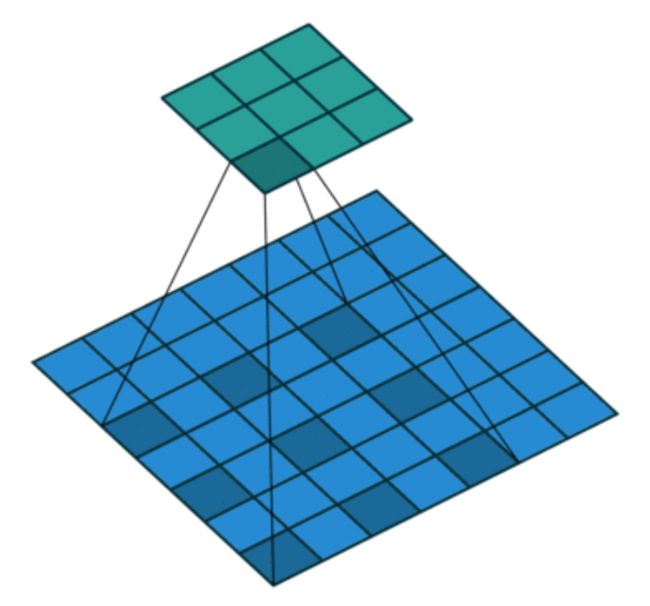
im2col是一个函数,将输入数据展开以适合滤波器(权重)。如下图所示,对 3 维的输入数据应用im2col后,数据转换为 2 维矩阵(正确地讲,是把包含批数量的 4 维数据转换成了 2 维数据)
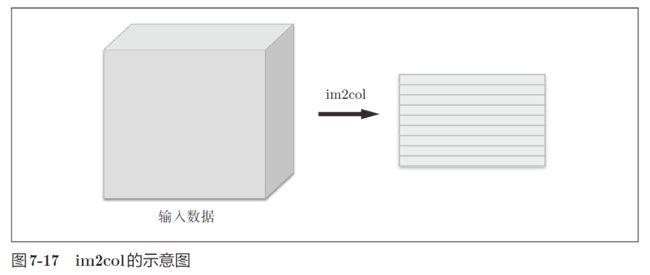
im2col对于输入数据,将应用滤波器的区域(3 维方块)横向展开为 1 行。im2col会在所有应用滤波器的地方进行这个展开处理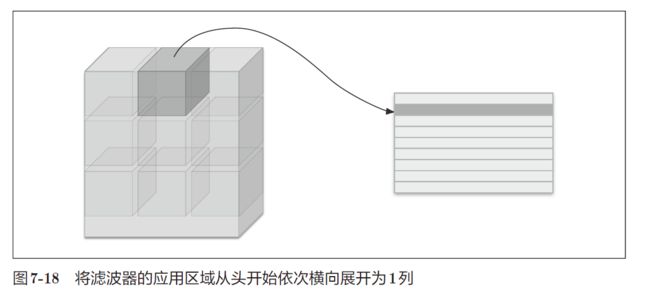
- 在上图中,为了便于观察,将步幅设置得很大,以使滤波器的应用区域不重叠。而在实际的卷积运算中,滤波器的应用区域几乎都是重叠的。在滤波器的应用区域重叠的情况下,使用
im2col展开后,展开后的元素个数会多于原方块的元素个数。因此,使用im2col的实现比普通的实现消耗更多内存。但是,汇总成一个大的矩阵进行计算,对计算机的计算颇有益处
- 在上图中,为了便于观察,将步幅设置得很大,以使滤波器的应用区域不重叠。而在实际的卷积运算中,滤波器的应用区域几乎都是重叠的。在滤波器的应用区域重叠的情况下,使用
- 下面写一下变换后的各个矩阵的形状以便理解:
- 输入数据: ( N , C , H , W ) (N, C, H, W) (N,C,H,W)
im2col转换之后的输入数据: ( N × O H × O W , C × F H × F W ) (N \times OH\times OW, C\times FH\times FW) (N×OH×OW,C×FH×FW)- 滤波器: ( F N , C , F H , F W ) (FN, C, FH, FW) (FN,C,FH,FW)
- F N FN FN 个滤波器转换之后的矩阵: ( C × F H × F W , F N ) (C\times FH\times FW, FN) (C×FH×FW,FN)
- 偏置 b b b: ( F N , ) (FN, ) (FN,)
- 输出数据 (2维): ( N × O H × O W , F N ) (N \times OH\times OW, FN) (N×OH×OW,FN). 在输出数据 (2维) 中,矩阵的一列即为输入特征图经过一个滤波器之后的结果
- 输出数据: ( N , F N , O H , O W ) (N, FN, OH, OW) (N,FN,OH,OW)
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
N, C, H, W = input_data.shape
out_h = (H + 2 * pad - filter_h) // stride + 1 # 向下取整
out_w = (W + 2 * pad - filter_w) // stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, out_h, out_w, filter_h, filter_w))
# x_min 和 y_min 用于界定一个滤波器作用的方块区域
for y in range(out_h):
y_min = y * stride
for x in range(out_w):
x_min = x * stride
col[:, :, y, x, :, :] = img[:, :, y_min:y_min+filter_h, x_min:x_min+filter_w]
col = col.transpose(0, 2, 3, 1, 4, 5).reshape(N*out_h*out_w, -1)
return col
- 当然,在反向传播的时候还需要
im2col函数的逆处理col2im函数。由于在卷积运算的过程中,滤波器的作用区域可能是重合的,因此 img 中的一个元素可能会多次出现在 col 中,根据链式法则,img 中元素的偏导即为 col 中所有该元素所在位置的偏导之和
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
N, C, H, W = input_shape # padding之前的图像大小
out_h = (H + 2 * pad - filter_h) // stride + 1
out_w = (W + 2 * pad - filter_w) // stride + 1
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 1, 2, 4, 5)
img = np.zeros((N, C, H + 2 * pad, W + 2 * pad))
for y in range(out_h):
y_min = y * stride
for x in range(out_w):
x_min = x * stride
# 要注意这里是 += 而非 = ,原因就是上面的那段话
img[:, :, y_min:y_min+filter_h, x_min:x_min+filter_w] += col[:, :, y, x, :, :]
return img[:, :, pad:H+pad, pad:W+pad]
卷积层的实现
正向传播
- 利用前面讲的
im2col进行快速矩阵运算
反向传播
- 反向传播类似于全连接层,唯一的区别就是在求得 d x dx dx 之后还要通过
col2im函数变换形状
- 简单推导一下反向传播的计算 (与全连接层的推导是一模一样的)
- 为了推理上方便书写,先引入克罗内克符号:
δ i , j = 1 i f i = j \delta_{i,j} = 1 \ \ \ \ \ \ \ \ \ \ \ \ \ if \ i = j δi,j=1 if i=j δ i , j = 0 i f i ≠ j \delta_{i,j} = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ if \ i \neq j δi,j=0 if i=j
下面正式进行推导:
∂ L ∂ w a b = ∑ i , j ∂ L ∂ y i j ∂ y i j ∂ w a b = ∑ i , j ∂ L ∂ y i j ∂ ( ∑ k ( x i k ∗ w k j ) + b j ) ∂ w a b = ∑ i , j ∂ L ∂ y i j x i k δ a k δ b j = ∑ i ∂ L ∂ y i b x i a ∴ ∂ L ∂ W = X T ⋅ ∂ L ∂ Y \begin{aligned} \frac{\partial L}{\partial w_{ab}} &= \sum_{i,j} \frac{\partial L}{\partial y_{ij}} \frac{\partial y_{ij}}{\partial w_{ab}} \\&= \sum_{i,j} \frac{\partial L}{\partial y_{ij}} \frac{\partial (\sum_{k} (x_{ik} * w_{kj}) + b_{j})}{\partial w_{ab}} \\&= \sum_{i,j} \frac{\partial L}{\partial y_{ij}} x_{ik } \delta_{ak} \delta_{bj} \\&= \sum_{i} \frac{\partial L}{\partial y_{ib}} x_{ia} \\ \therefore \frac{\partial L}{\partial W} &= X^T \cdot \frac{\partial L}{\partial Y} \end{aligned} ∂wab∂L∴∂W∂L=i,j∑∂yij∂L∂wab∂yij=i,j∑∂yij∂L∂wab∂(∑k(xik∗wkj)+bj)=i,j∑∂yij∂Lxikδakδbj=i∑∂yib∂Lxia=XT⋅∂Y∂L
∂ L ∂ x a b = ∑ i , j ∂ L ∂ y i j ∂ y i j ∂ x a b = ∑ i , j ∂ L ∂ y i j ∂ ( ∑ k ( x i k ∗ w k j ) + b j ) ∂ x a b = ∑ i , j ∂ L ∂ y i j w k j δ a i δ b k = ∑ j ∂ L ∂ y a j w b j ∴ ∂ L ∂ X = ∂ L ∂ Y ⋅ W T \begin{aligned} \frac{\partial L}{\partial x_{ab}} &= \sum_{i,j} \frac{\partial L}{\partial y_{ij}} \frac{\partial y_{ij}}{\partial x_{ab}} \\&= \sum_{i,j} \frac{\partial L}{\partial y_{ij}} \frac{\partial (\sum_{k} (x_{ik} * w_{kj}) + b_{j})}{\partial x_{ab}} \\&= \sum_{i,j} \frac{\partial L}{\partial y_{ij}} w_{kj } \delta_{ai} \delta_{bk} \\&= \sum_{j} \frac{\partial L}{\partial y_{aj}} w_{bj} \\ \therefore \frac{\partial L}{\partial X} &= \frac{\partial L}{\partial Y} \cdot W^T \end{aligned} ∂xab∂L∴∂X∂L=i,j∑∂yij∂L∂xab∂yij=i,j∑∂yij∂L∂xab∂(∑k(xik∗wkj)+bj)=i,j∑∂yij∂Lwkjδaiδbk=j∑∂yaj∂Lwbj=∂Y∂L⋅WT
∂ L ∂ b a = ∑ i , j ∂ L ∂ y i j ∂ y i j ∂ b a = ∑ i , j ∂ L ∂ y i j ∂ ( ∑ k ( x i k ∗ w k j ) + b j ) ∂ b a = ∑ i , j ∂ L ∂ y i j δ a j = ∑ i ∂ L ∂ y i a ∴ ∂ L ∂ B = ∂ L ∂ Y 的 第 0 轴 上 的 和 \begin{aligned} \frac{\partial L}{\partial b_{a}} &=\sum_{i,j} \frac{\partial L}{\partial y_{ij}} \frac{\partial y_{ij}}{\partial b_{a}} \\&= \sum_{i,j} \frac{\partial L}{\partial y_{ij}} \frac{\partial (\sum_{k} (x_{ik} * w_{kj}) + b_{j})}{\partial b_{a}} \\&= \sum_{i,j} \frac{\partial L}{\partial y_{ij}} \delta_{aj}\\&= \sum_{i} \frac{\partial L}{\partial y_{ia}} \\ \therefore \frac{\partial L}{\partial B} &= \frac{\partial L}{\partial Y} 的第0轴上的和 \end{aligned} ∂ba∂L∴∂B∂L=i,j∑∂yij∂L∂ba∂yij=i,j∑∂yij∂L∂ba∂(∑k(xik∗wkj)+bj)=i,j∑∂yij∂Lδaj=i∑∂yia∂L=∂Y∂L的第0轴上的和
- 为了推理上方便书写,先引入克罗内克符号:
代码实现
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
self.x = None
self.col = None
self.col_W = None
self.db = None
self.dW = None
def forward(self, x):
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
out_h = (H + 2 * self.pad - FH) // self.stride + 1
out_w = (W + 2 * self.pad - FW) // self.stride + 1
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T
out = (np.dot(col, col_W) + self.b).reshape(N, out_h, out_w, FN).transpose(0, 3, 1, 2)
self.x = x
self.col = col
self.col_W = col_W
return out
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)
self.db = dout.sum(axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.T.reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
Max 池化层的实现
正向传播
- 池化层的实现和卷积层相同,都使用
im2col展开输入数据。不过,池化的情况下,在通道方向上是独立的,这一点和卷积层不同。池化的应用区域应该按通道单独展开
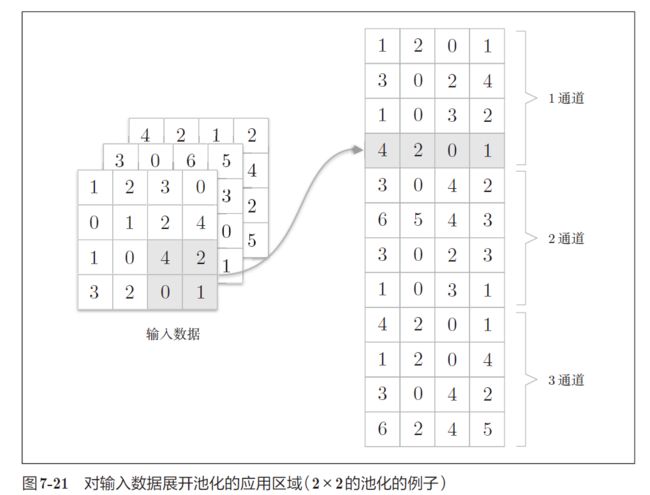
也就是说, ( N , C , H , W ) (N, C, H, W) (N,C,H,W) 的输入数据在im2col之后形状变为 ( N × O H × O W , C × F H × F W ) (N \times OH\times OW, C\times FH\times FW) (N×OH×OW,C×FH×FW),因此还要多加一步,将其 reshape 为 ( N × C × O H × O W , F H × F W ) (N \times C \times OH \times OW, FH \times FW) (N×C×OH×OW,FH×FW) - 像这样展开之后,只需对展开的矩阵求各行的最大值,并转换为合适的形状即可。转换为最大值之后的矩阵形状为 ( N × C × O H × O W , 1 ) (N \times C \times OH \times OW, 1) (N×C×OH×OW,1),最后将其 reshape 为 ( N , C , O H , O W ) (N , C, OH, OW) (N,C,OH,OW) 即可
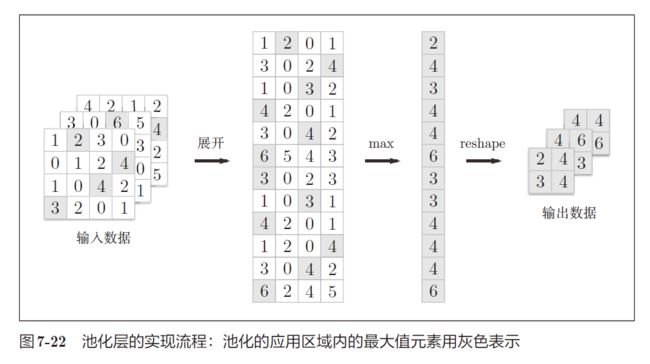
反向传播
- 反向传播类似于
Relu的反向传播,只要在正向传播时保存好各个滤波器中最大值的索引位置即可
代码实现
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.mask = None
def forward(self, x):
N, C, H, W = x.shape
out_h = (H + 2 * self.pad - self.pool_h) // self.stride + 1
out_w = (W + 2 * self.pad - self.pool_w) // self.stride + 1
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(N, out_h * out_w, C, self.pool_h * self.pool_w).transpose(0, 2, 1, 3).reshape(N * C * out_h * out_w, self.pool_h * self.pool_w)
mask = np.argmax(col, axis=1)
out = col[np.arange(mask.size), mask]
out = out.reshape(N, C, out_h, out_w)
self.mask = mask
self.input_shape = x.shape
return out
def backward(self, dout):
N, C, H, W = self.input_shape
out_h = (H + 2 * self.pad - self.pool_h) // self.stride + 1
out_w = (W + 2 * self.pad - self.pool_w) // self.stride + 1
dout = dout.reshape(N * C * out_h * out_w)
dcol = np.zeros((N * C * out_h * out_w, self.pool_h * self.pool_w))
dcol[np.arange(self.mask.size), self.mask] = dout
dcol = dcol.reshape(N, C, out_h * out_w, self.pool_h * self.pool_w).transpose(0, 2, 1, 3).reshape(N * out_h * out_w, C * self.pool_h * self.pool_w)
dx = col2im(dcol, self.input_shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
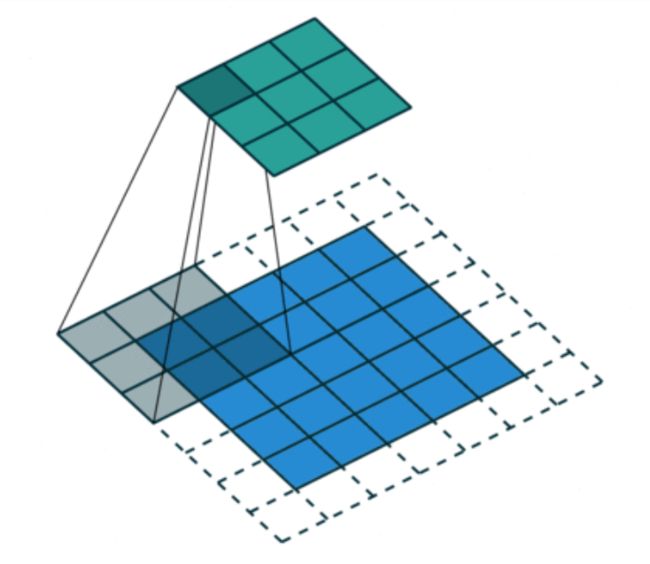
空洞卷积 (Dilated Convolution)
参考:https://www.zhihu.com/question/54149221
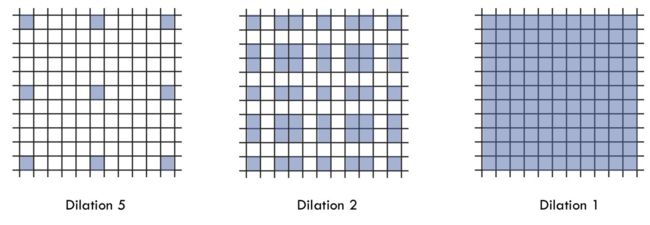
- 空洞卷积最初是为解决图像分割而提出的。常见的图像分割算法通常使用池化层来增大感受野,同时也缩小了特征图尺寸,然后再利用上采样还原图像尺寸。特征图缩小再放大的过程造成了精度损失。而空洞卷积则可以在增大感受野的同时保持特征图的尺寸不变,解决了这个问题
空洞卷积
缺陷:
- 网格效应 (Gridding Effect):由于空洞卷积是一种稀疏的采样方式,当多个空洞卷积叠加时,有些像素根本没有被利用,会损失信息的连续性与相关性
- 远距离的信息没有相关性
- 大的空洞数 (dilation rate) 对于大物体分割与检测有利,但是对于小物体则有弊无利,如何处理好多尺度问题的检测,是空洞卷积设计的重点
Hybrid Dilated Convolution (HDC)
参考:https://www.zhihu.com/question/54149221
- 为了弥补空洞卷积的缺陷,HDC 被设计了出来
HDC 的设计准则:
- 叠加卷积的 dilation rate 不能有大于 1 的公约数
- 将 dilation rate 设计成锯齿状结构,例如 [1, 2, 5, 1, 2, 5] 的循环结构
- 满足下列式子:
M i = m a x ⌈ M i + 1 − 2 r i , M i + 1 − 2 ( M i + 1 − r i ) , r i ⌉ M_i = max \lceil M_{i+1} - 2r_i, M_{i+1} - 2(M_{i+1} - r_i), r_i \rceil Mi=max⌈Mi+1−2ri,Mi+1−2(Mi+1−ri),ri⌉其中 r i r_i ri 是 i i i 层的 dilation rate , M i M_i Mi 是在 i i i 层的最大 dilation rate,那么假设总共有 n n n 层的话,默认 M n = r n M_n=r_n Mn=rn
Deformable Convolution (可变形卷积)
- paper: Deformable Convolutional Networks
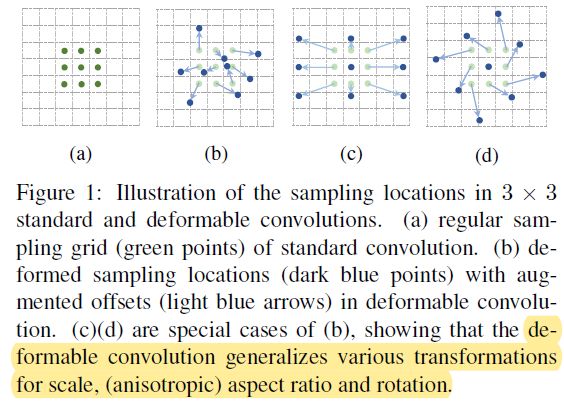
Deformable Convolution
- 标准 2D 卷积:
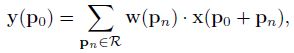 其中, y y y 为输出特征图, x x x 为输入特征图, p 0 p_0 p0 为特征图上的某个位置, w w w 为卷积核权重, p n p_n pn 为卷积核上的某个位置, R \mathcal R R 为卷积核覆盖位置的偏置,例如 3 × 3 3\times3 3×3 卷积对应的 R \mathcal R R 为
其中, y y y 为输出特征图, x x x 为输入特征图, p 0 p_0 p0 为特征图上的某个位置, w w w 为卷积核权重, p n p_n pn 为卷积核上的某个位置, R \mathcal R R 为卷积核覆盖位置的偏置,例如 3 × 3 3\times3 3×3 卷积对应的 R \mathcal R R 为
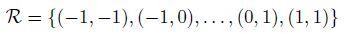
- 可变形卷积:
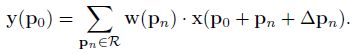 其中, Δ p n \Delta p_n Δpn 为卷积核的位置偏移量。偏移量 p n p_n pn 由另一个卷积分支得到,一般是小数,因此需要使用双线性插值得到 x ( p 0 + p n + Δ p n ) x(p_0+p_n+\Delta p_n) x(p0+pn+Δpn):
其中, Δ p n \Delta p_n Δpn 为卷积核的位置偏移量。偏移量 p n p_n pn 由另一个卷积分支得到,一般是小数,因此需要使用双线性插值得到 x ( p 0 + p n + Δ p n ) x(p_0+p_n+\Delta p_n) x(p0+pn+Δpn):
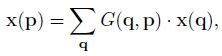 其中, q q q 需要枚举输入特征图 x x x 上的每一个位置, G G G 为双线性插值核:
其中, q q q 需要枚举输入特征图 x x x 上的每一个位置, G G G 为双线性插值核:
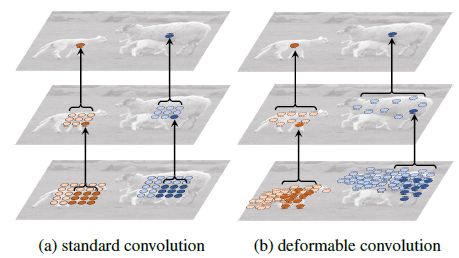
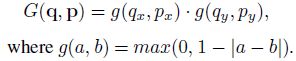 如下图所示,卷积核的位置偏移量由绿色的卷积分支得到,该分支输出的 offset fields 大小与输入特征图一样,通道数则变为原来的两倍,用来代表输入特征图上每个点对应的 x x x 和 y y y 轴偏移量
如下图所示,卷积核的位置偏移量由绿色的卷积分支得到,该分支输出的 offset fields 大小与输入特征图一样,通道数则变为原来的两倍,用来代表输入特征图上每个点对应的 x x x 和 y y y 轴偏移量
Deformable RoI Pooling (Deformable-RFCN)
虽然 RoI Pooling 已经属于目标检测领域了,但由于 Deformable RoI Pooling 是和 Deformable Convolution 在一篇论文中被提出的,因此还是一起介绍一下,不熟悉目标检测可以跳过
- 标准 RoI Pooling:
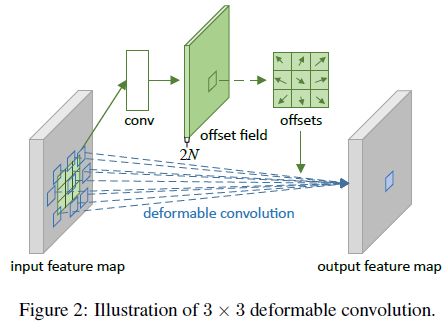
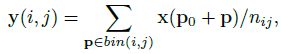 其中, y y y 为 k × k k\times k k×k 的输出特征图 (i.e. 感兴趣区域特征图), x x x 为输入特征图。RoI 大小为 w × h w\times h w×h,被划分为 k × k k\times k k×k 个子区域。 p 0 p_0 p0 为 RoI 的左上位置, b i n ( i , j ) bin(i,j) bin(i,j) ( 0 ≤ i , j ≤ k 0\leq i,j\leq k 0≤i,j≤k) 为 RoI 的某个子区域, n i j n_{ij} nij 为该子区域包含的像素点个数
其中, y y y 为 k × k k\times k k×k 的输出特征图 (i.e. 感兴趣区域特征图), x x x 为输入特征图。RoI 大小为 w × h w\times h w×h,被划分为 k × k k\times k k×k 个子区域。 p 0 p_0 p0 为 RoI 的左上位置, b i n ( i , j ) bin(i,j) bin(i,j) ( 0 ≤ i , j ≤ k 0\leq i,j\leq k 0≤i,j≤k) 为 RoI 的某个子区域, n i j n_{ij} nij 为该子区域包含的像素点个数 - Deformable RoI Pooling:
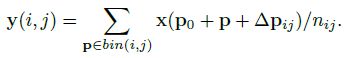 其中, Δ p i j \Delta p_{ij} Δpij 为卷积核子区域 ( i , j ) (i,j) (i,j) 的位置偏移量,也就是说,每个子区域中所有点的偏移量都是一样的。类似可变形卷积, x ( p 0 + p + Δ p i j ) x(p_0+p+\Delta p_{ij}) x(p0+p+Δpij) 也需要经过双线性插值得到。如下图所示,每个子区域的位置偏移量由绿色的网络分支得到。首先使用标准的 RoI Pooling 生成 C × k × k C\times k\times k C×k×k 的特征图,然后使用全连接层得到 C × k × k × 2 C\times k\times k\times2 C×k×k×2 个归一化偏移量 Δ p ^ i j \Delta\hat p_{ij} Δp^ij,接着将 Δ p ^ i j \Delta\hat p_{ij} Δp^ij 与 ( w , h ) (w,h) (w,h) 作逐元素乘再乘上尺度因子 γ = 0.1 \gamma=0.1 γ=0.1 后得到最终的位置偏移量 Δ p i j \Delta p_{ij} Δpij ( Δ p i j = γ ⋅ Δ p ^ i j ⊙ ( w , h ) \Delta p_{ij}=\gamma\cdot\Delta\hat p_{ij}\odot(w,h) Δpij=γ⋅Δp^ij⊙(w,h)) ,这里与 ( w , h ) (w,h) (w,h) 相乘是为了使得位置偏移量的学习独立于 RoI 的大小, γ \gamma γ 为经验参数
其中, Δ p i j \Delta p_{ij} Δpij 为卷积核子区域 ( i , j ) (i,j) (i,j) 的位置偏移量,也就是说,每个子区域中所有点的偏移量都是一样的。类似可变形卷积, x ( p 0 + p + Δ p i j ) x(p_0+p+\Delta p_{ij}) x(p0+p+Δpij) 也需要经过双线性插值得到。如下图所示,每个子区域的位置偏移量由绿色的网络分支得到。首先使用标准的 RoI Pooling 生成 C × k × k C\times k\times k C×k×k 的特征图,然后使用全连接层得到 C × k × k × 2 C\times k\times k\times2 C×k×k×2 个归一化偏移量 Δ p ^ i j \Delta\hat p_{ij} Δp^ij,接着将 Δ p ^ i j \Delta\hat p_{ij} Δp^ij 与 ( w , h ) (w,h) (w,h) 作逐元素乘再乘上尺度因子 γ = 0.1 \gamma=0.1 γ=0.1 后得到最终的位置偏移量 Δ p i j \Delta p_{ij} Δpij ( Δ p i j = γ ⋅ Δ p ^ i j ⊙ ( w , h ) \Delta p_{ij}=\gamma\cdot\Delta\hat p_{ij}\odot(w,h) Δpij=γ⋅Δp^ij⊙(w,h)) ,这里与 ( w , h ) (w,h) (w,h) 相乘是为了使得位置偏移量的学习独立于 RoI 的大小, γ \gamma γ 为经验参数
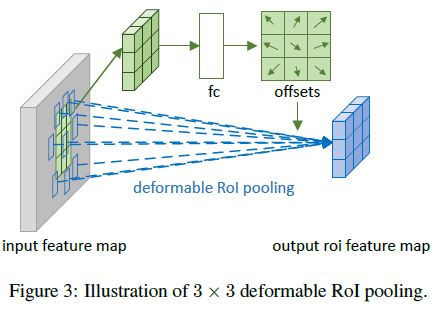
- Position-Sensitive (PS) RoI Pooling: 全连接层的使用会极大地增加网络参数,增加过拟合风险。为此,作者将可变形 RoI 池化和 R-FCN 的位置敏感 RoI 池化相结合,提出了可变形位置敏感 RoI 池化,其中上方的卷积分支输出归一化位置偏移量,经过与可变形 RoI 池化同样的过程后得到最终的位置偏移量:
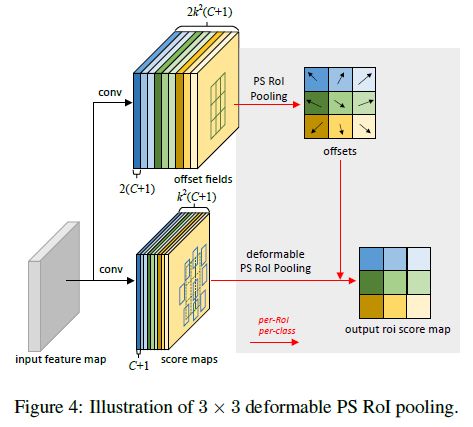
Octave Convolution (降频卷积)
- paper: Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution
- 在图像处理领域,图像可以分为描述基础背景结构的低频特征与描述快速变化细节的高频特征两部分,其中高频特征占据了主要的图像信息。与此类似,卷积特征也可以分为高频特征与低频特征两种,Octave 卷积通过相邻位置的特征共享,减小了低频特征的尺寸,进而减小了特征的冗余,提升了卷积计算的速度
Octave 一词本意是八音阶,在音乐里每降低八个音阶,频率就会减半,而 Octave 卷积的思想正是通过降低了低频率特征的尺寸,从而减少了计算量,因此取名 Octave 卷积
- 实验结果表明,Octave 卷积可以即插即用,能够方便地部署到 ResNet、MobileNet 等多种经典的卷积结构中,并且性能会有明显的提升
降频卷积
- 对于一个特征图 X X X,降频卷积按照比例 α ∈ [ 0 , 1 ] \alpha\in[0,1] α∈[0,1] 将其按通道分为两个部分, α \alpha α 的通道为低频通道 X L X^L XL, 1 − α 1-\alpha 1−α 的通道为高频通道 X H X^H XH (i.e. X = [ X H , X L ] X=[X^H,X^L] X=[XH,XL]),随后将低频通道的长宽各缩减一半,由此得到特征图的高频和低频两个部分
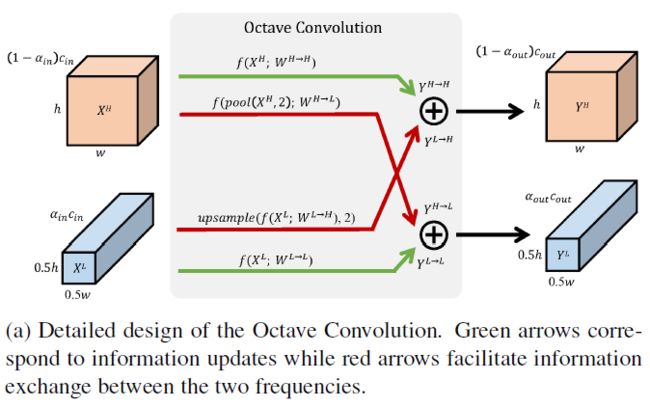
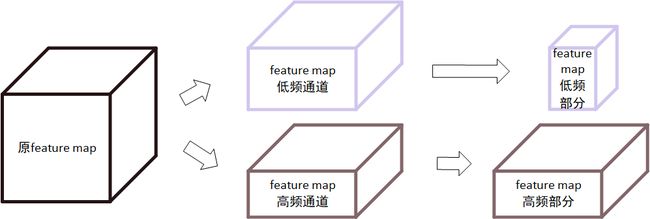 为了处理这种结构的特征图,其使用了如下所示的降频卷积操作:
为了处理这种结构的特征图,其使用了如下所示的降频卷积操作:
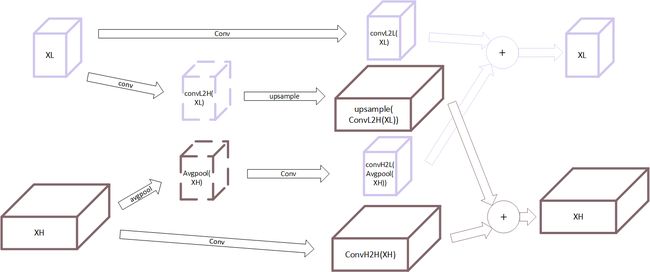
- 首先考虑低频部分输入,该部分进行两个部分的操作:
- (1) X L → X H X^L \to X^H XL→XH: 从低频到高频,首先使用指定卷积核 W L → H W^{L \to H} WL→H 进行卷积,随后进行上采样操作生成与高频部分长宽相同的特征图,最终产生 Y L → H = U p s a m p l e ( C o n v ( X L , W L → H ) , 2 ) Y^{L\to H} = Upsample(Conv(X^L,W^{L \to H}),2) YL→H=Upsample(Conv(XL,WL→H),2)
- (2) X L → X L X^L \to X^L XL→XL: 从低频到低频,这个部分为直接进行卷积操作 Y L → L = C o n v ( X L , W L → L ) Y^{L \to L} = Conv(X^L,W^{L \to L}) YL→L=Conv(XL,WL→L)
- 随后考虑高频部分输入,与低频部分类似有两个部分的操作:
- (1) X H → X H X^H \to X^H XH→XH: 从高频到高频,直接进行卷积操作 Y H → H = C o n v ( X H , W H → H ) Y^{H \to H} = Conv(X^H,W^{H \to H}) YH→H=Conv(XH,WH→H)
- (2) X H → X L X^H \to X^L XH→XL: 从高频到低频,首先进行步长和卷积核均为 2 的平均值池化,再进行卷积操作,生成与 Y L Y^L YL 通道数相同的特征图,最终产生 Y H → L = c o n v ( a v g p o o l ( X H , 2 ) , W H → L ) ) Y^{H \to L} = conv(avgpool(X^H,2),W^{H \to L})) YH→L=conv(avgpool(XH,2),WH→L))
- 最终共有 W H → H , W H → L , W L → H , W L → L W^{H\to H},W^{H\to L},W^{L\to H},W^{L\to L} WH→H,WH→L,WL→H,WL→L 4 个权值。高频和低频输出为
Y L = Y H → L + Y L → L = c o n v ( a v g p o o l ( X H , 2 ) , W H → L ) ) + C o n v ( X L , W L → L ) Y H = Y H → H + Y L → H = C o n v ( X H , W H → H ) + U p s a m p l e ( C o n v ( X L , W L → H ) , 2 ) Y^L = Y^{H \to L} + Y^{L \to L} = conv(avgpool(X^H,2),W^{H \to L})) + Conv(X^L,W^{L \to L}) \\ Y^H = Y^{H \to H} +Y^{L \to H} = Conv(X^H,W^{H \to H}) + Upsample(Conv(X^L,W^{L \to H}),2) YL=YH→L+YL→L=conv(avgpool(XH,2),WH→L))+Conv(XL,WL→L)YH=YH→H+YL→H=Conv(XH,WH→H)+Upsample(Conv(XL,WL→H),2) - 另外进行使用时,在网络的输入和输出需要将两个频率上的 Tensor 聚合,做法如下:
- (1) 网络输入:取 α i n = 0 , α o u t = α \alpha_{in}=0,\alpha_{out}=\alpha αin=0,αout=α,即有 X H = X , X L = 0 X^H=X,X^L=0 XH=X,XL=0,仅进行 H → L H\to L H→L 和 H → H H\to H H→H 操作,输出的高频和低频部分分别为 Y H = Y H → H Y^H = Y^{H \to H} YH=YH→H 和 Y L = Y H → L Y^L = Y^{H \to L} YL=YH→L
- (2) 网络输出:取 α i n = α , α o u t = 0 \alpha_{in}=\alpha,\alpha_{out}=0 αin=α,αout=0,仅进行 L → H L\to H L→H 和 H → H H\to H H→H 操作,最终输出为 Y = Y L → H + Y H → H Y = Y^{L \to H} + Y^{H \to H} Y=YL→H+YH→H
- 其余情况均取 α i n = α o u t = α \alpha_{in}=\alpha_{out}=\alpha αin=αout=α
计算量分析
- 设输入特征图尺寸为 C i n × W × H C_{in}\times W\times H Cin×W×H,输出特征图尺寸为 C o u t × W × H C_{out}\times W\times H Cout×W×H,卷积核尺寸为 C o u t × C i n × K × K C_{out}\times C_{in}\times K\times K Cout×Cin×K×K
- 标准卷积的计算量为
C c o n v = C o u t × W × H × C i n × K × K C_{conv}=C_{out}\times W\times H\times C_{in}\times K\times K Cconv=Cout×W×H×Cin×K×K - 降频卷积的四部分计算量分别为:
C L → L = α 2 × ( C o u t × W 2 × H 2 ) × ( C i n × K × K ) = α 2 4 × C c o n v C L → H = ( ( 1 − α ) × C o u t × W 2 × H 2 ) × ( α × C i n × K × K ) = α ( 1 − α ) 4 × C c o n v C H → L = ( α × C o u t × W 2 × H 2 ) × ( ( 1 − α ) × C i n × K × K ) = α ( 1 − α ) 4 × C c o n v C H → H = ( ( 1 − α ) × C o u t × W × H ) × ( ( 1 − α ) × C i n × K × K ) = ( 1 − α ) 2 × C c o n v C_{L \to L} = \alpha^2 \times (C_{out}\times \frac{W}{2} \times \frac{H}{2}) \times (C_{in} \times K \times K) = \frac{\alpha^2}{4} \times C_{conv}\\ C_{L \to H} = ((1 - \alpha) \times C_{out} \times \frac{W}{2} \times \frac{H}{2}) \times ( \alpha \times C_{in} \times K \times K) = \frac{\alpha(1-\alpha)}{4} \times C_{conv}\\ C_{H \to L} = (\alpha \times C_{out} \times \frac{W}{2} \times \frac{H}{2}) \times ((1 - \alpha) \times C_{in} \times K \times K) = \frac{\alpha(1-\alpha)}{4} \times C_{conv}\\ C_{H \to H} = ((1 - \alpha) \times C_{out} \times W \times H) \times ((1 - \alpha) \times C_{in} \times K \times K) = (1 - \alpha)^2 \times C_{conv} CL→L=α2×(Cout×2W×2H)×(Cin×K×K)=4α2×CconvCL→H=((1−α)×Cout×2W×2H)×(α×Cin×K×K)=4α(1−α)×CconvCH→L=(α×Cout×2W×2H)×((1−α)×Cin×K×K)=4α(1−α)×CconvCH→H=((1−α)×Cout×W×H)×((1−α)×Cin×K×K)=(1−α)2×Cconv总计算量
C o c t a v e C c o n v = α 2 + 2 α ( 1 − α ) + 4 ( 1 − α ) 2 4 = 1 − 3 4 α ( 2 − α ) \frac{C_{octave}}{C_{conv}} = \frac{\alpha^2 + 2\alpha(1-\alpha) + 4 (1 - \alpha)^2}{4} = 1 - \frac{3}{4}\alpha(2- \alpha) CconvCoctave=4α2+2α(1−α)+4(1−α)2=1−43α(2−α)在 α ∈ [ 0 , 1 ] \alpha\in[0,1] α∈[0,1] 中单调递减,当取 α = 1 \alpha=1 α=1 时,有 C o c t a v e C c o n v = 1 4 \frac{C{octave}}{C{conv}} = \frac{1}{4} CconvCoctave=41
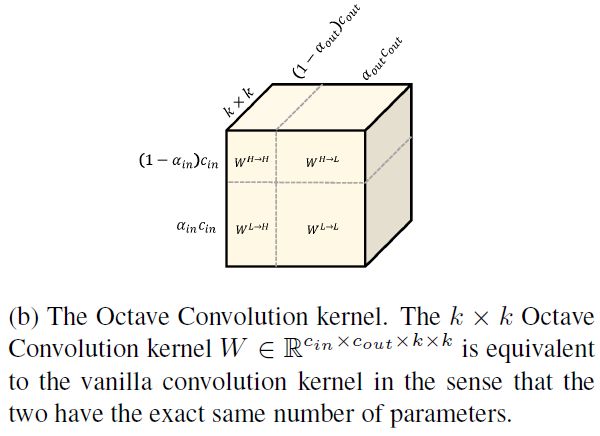
参数量分析
- 如下图所示,降频卷积的参数量与标准卷积一样,均为 C o u t × C i n × K × K C_{out} \times C_{in} \times K \times K Cout×Cin×K×K,因此该方法无法减少参数量
Transposed convolution (转置卷积)
- 当我们想要进行卷积操作的反向变换时就可以使用转置卷积,它可以将具有某个卷积操作输出 shape 的张量变换为具有该卷积操作输入 shape 的张量,同时还能与该卷积操作具有相同的连通模式。例如,我们可以将转置卷积用作卷积自编码器的解码层,或者是单纯地用转置卷积将特征图投影到高维空间
Convolution as a matrix operation
- 考虑上述卷积操作,如果将输入 x x x 和输出 y y y 都拉直为向量,那么我们就可以将卷积操作用一个矩阵乘法 y = C x y=Cx y=Cx 来表示,其中稀疏矩阵 C C C 为
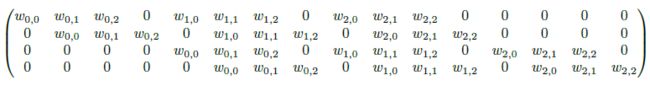 也就是说,上述卷积操作可以看作在正向传播时输入乘 C C C,在反向传播时梯度乘 C T C^T CT; C C C 和 C T C^T CT 分别在正向和反向传播时被使用
也就是说,上述卷积操作可以看作在正向传播时输入乘 C C C,在反向传播时梯度乘 C T C^T CT; C C C 和 C T C^T CT 分别在正向和反向传播时被使用
Transposed convolution
- 转置卷积就是交换了卷积操作的前向和反向过程,也就是在前向传播时乘 C T C^T CT,反向传播时乘 C C C
可以看出,转置卷积仅仅是为了恢复卷积操作的 shape,而非真的是卷积操作的逆操作,因此不太推荐将其称为 “反卷积” (Deconvolution)
等价的卷积操作
- 每个转置卷积都可以用一个等价的卷积操作表示,下面将会列举出几种情况下转置卷积等价的卷积操作
转置卷积的工程实现
- 每个转置卷积都可以用一个等价的卷积操作表示,这意味着我们可以直接用等价的卷积操作去实现转置卷积。但这个等价的卷积操作需要给输入添加很多零行和零列,这使得等价的卷积操作往往不那么高效,因此在实现时一般不会采用等价的卷积操作,而是直接去实现转置卷积操作
- 我们可以将转置卷积的 input 看作卷积操作反向传播时输入的梯度,也就是说将卷积层的反向传播和正向传播函数对调一下就行了。具体而言,如果使用
im2col和col2im进行实现,那么在转置卷积的正向传播中就将 ( N , F N , O H , O W ) (N, FN, OH, OW) (N,FN,OH,OW) 的输入 reshape 为 ( N × O H × O W , F N ) (N\times OH\times OW,FN) (N×OH×OW,FN),与卷积核组成的 ( F N , C × F H × F W ) (FN,C\times FH\times FW) (FN,C×FH×FW) 的矩阵相乘,得到 ( N × O H × O W , C × F H × F W ) (N\times OH\times OW,C\times FH\times FW) (N×OH×OW,C×FH×FW) 的输出,再用col2im函数还原为 ( N , C , H , W ) (N,C,H,W) (N,C,H,W) 的输出即可;而转置卷积的反向传播过程则与卷积的正向传播过程一致
No zero padding, unit strides, transposed
- 我们还是以下图 i = 4 , k = 3 , s = 1 , p = 0 i=4,k=3,s=1,p=0 i=4,k=3,s=1,p=0 的卷积操作为例:
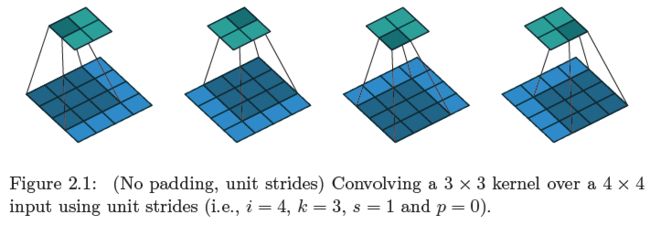 该卷积操作对应的 C C C 矩阵为:
该卷积操作对应的 C C C 矩阵为:
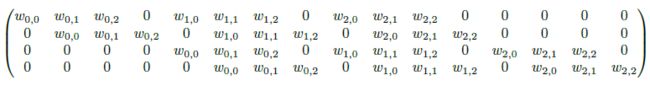
- 现在考虑该卷积操作对应的转置卷积操作 y = C T x y=C^Tx y=CTx,其中 y ∈ R 16 , x ∈ R 4 y\in\R^{16},x\in\R^4 y∈R16,x∈R4。由该矩阵乘法可知, y y y 的第一个元素 ( 4 × 4 4\times4 4×4 输出的左上角元素) 为 w 0 , 0 x 0 w_{0,0}x_0 w0,0x0,第四个元素 ( 4 × 4 4\times4 4×4 输出的右上角元素) 为 w 0 , 2 x 1 w_{0,2}x_1 w0,2x1… 因此可以想到转置卷积等价的卷积操作需要对 x x x 进行 zero padding 并且 padding 大小 p ′ = k − 1 p'=k-1 p′=k−1,这样在输出 y y y 的左上角元素时卷积核就会只与 x 0 x_0 x0 连通,输出 y y y 的右上角元素时卷积核就会只与 x 1 x_1 x1 连通。综合考虑下,等价的卷积操作如下图所示:
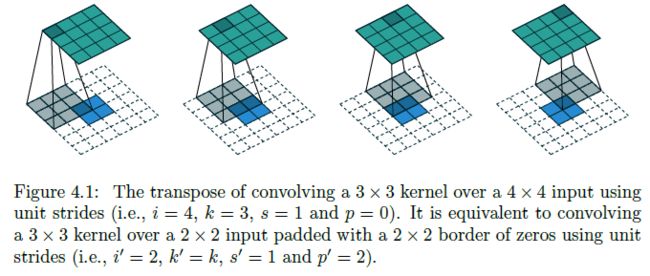
- 再进一步,我们可以总结出如下规律:No zero padding, unit strides 的卷积操作对应的转置卷积为 Full padding, unit strides 的卷积操作

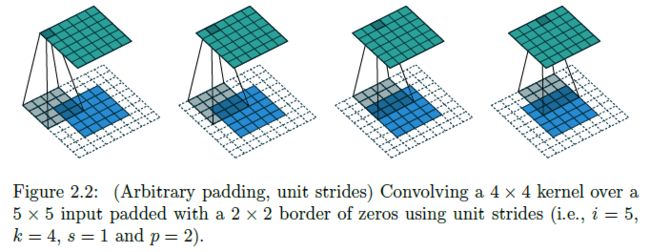
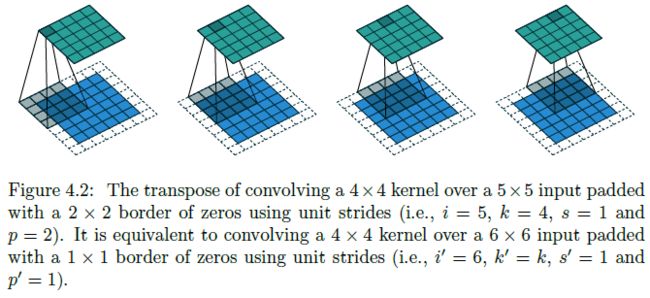
Zero padding, unit strides, transposed
Half (same) padding, transposed
- 考虑 Zero padding, unit strides 的一种特殊情况:当 o ′ = o o'=o o′=o (i.e. 2 p = k − 1 2p=k-1 2p=k−1) 时,转置卷积操作与卷积操作相同:
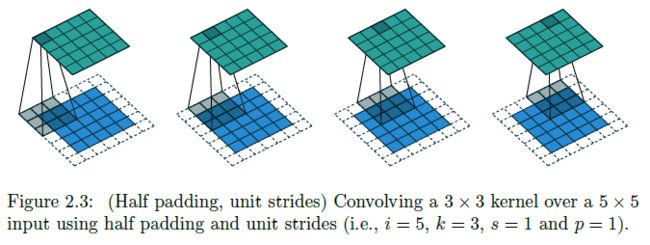
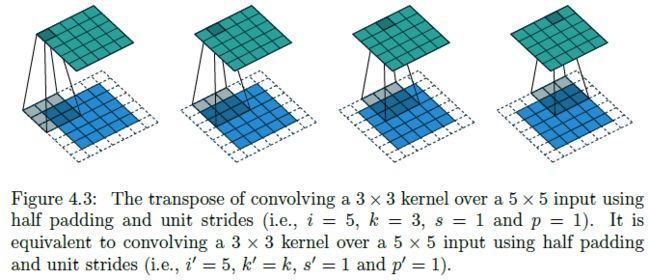
- Half padding, unit strides 的卷积操作对应的转置卷积仍为 Half padding, unit strides 的卷积操作
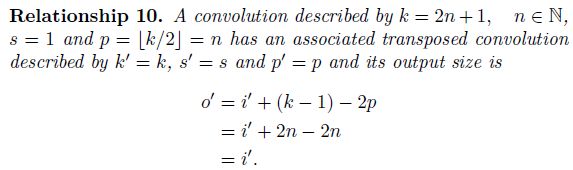
Full padding, transposed
- 再考虑 Zero padding, unit strides 的一种特殊情况: p = k − 1 p=k-1 p=k−1 (i.e. full padding):
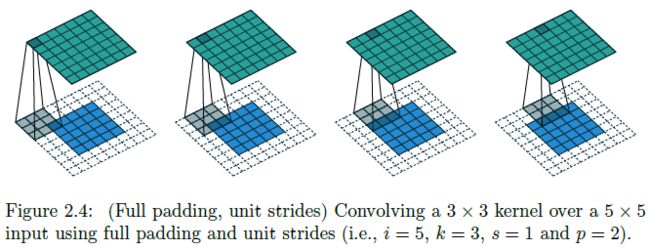
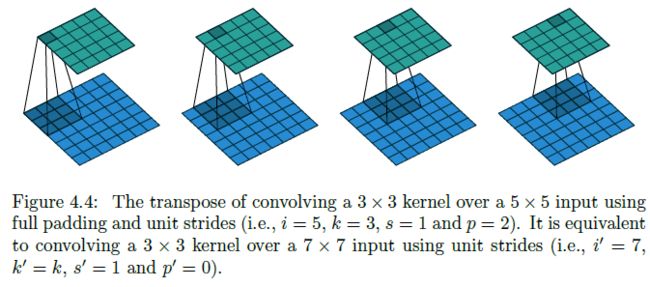
- Full padding, unit strides 的卷积操作对应的转置卷积为 Zero padding, unit strides 的卷积操作

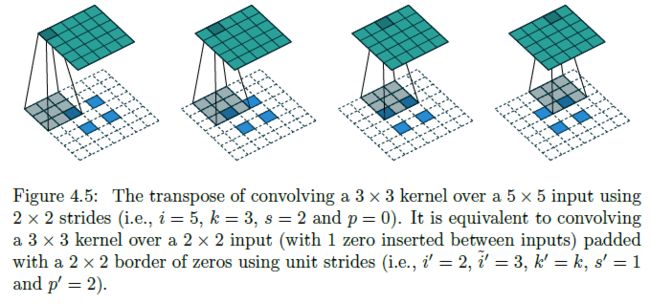
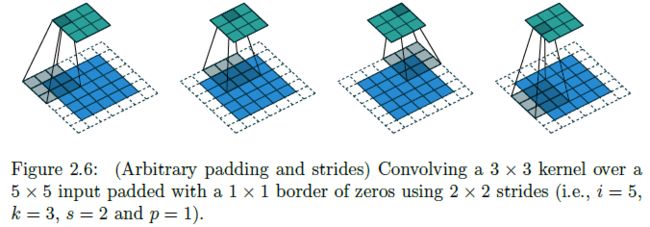
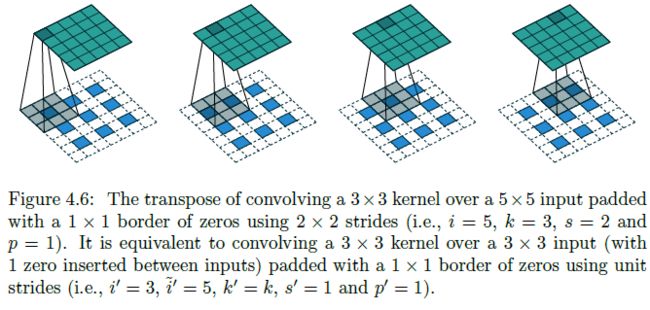
No zero padding, non-unit strides, transposed
- No zero padding, non-unit strides 的卷积操作对应的转置卷积为在 stretched input 上进行的 Zero padding, unit strides 的卷积操作

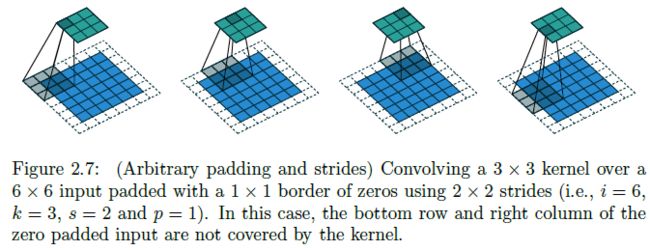
Zero padding, non-unit strides, transposed
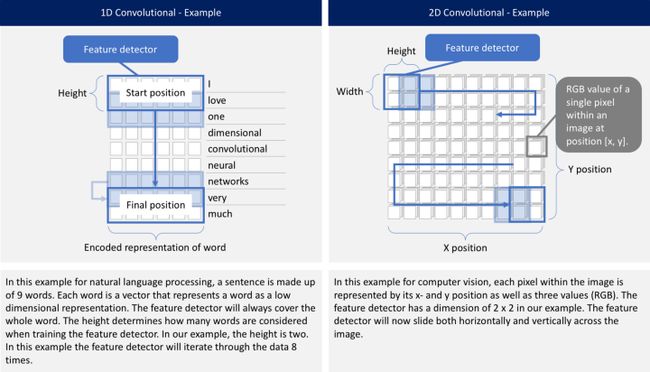
1D Conv
1D Conv
nn.Conv1d
torch.nn.Conv1d(
in_channels, # 输入信号的通道。在文本分类中,即为词向量的维度
out_channels, # 卷积产生的通道。有多少个 out_channels,就需要多少个 1 维卷积
kernel_size, # 卷积核的尺寸 (Height),卷积核的大小为 (k,),第二个维度是由 in_channels 来决定的,所以实际上卷积大小为 kernel_size * in_channels
stride=1, # 卷积步长
padding=0, # 输入的每一条边补充 0 的层数
dilation=1, # 卷积核元素之间的间距
groups=1, # 从输入通道到输出通道的阻塞连接数
bias=True # 添加偏置
)
Example
conv1 = nn.Conv1d(
in_channels=256,
out_channels=100,
kernel_size=2
)
input = torch.randn(32, 35, 256) # batch_size x text_len x embedding_size
input = input.permute(0, 2, 1) # batch_size x embedding_size x text_len
out = conv1(input) # batch_size x out_channels x (text_len + 2 * padding - kernel_size) // stride + 1
print(out.size()) # 32 x 100 x 34
参考文献
- 《深度学习入门 – 基于 Python 的理论与实现》
- 吴恩达深度学习视频
- A guide to convolution arithmetic for deep learning
- Deformable Convolution
- Octave 卷积
- pytorch 之 nn.Conv1d 详解
- Introduction to 1D Convolutional Neural Networks in Keras for Time Sequences