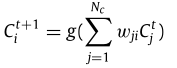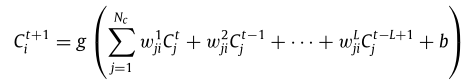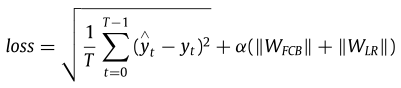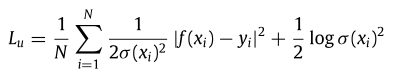CNN-FCM:系统建模用于提高深度学习在时间序列预测中的稳定性
1. 文章信息
文章题为《CNN-FCM: System modeling promotes stability of deep learning in time series prediction》是一篇有关时间序列预测的文章,发表在Knowledge-Based Systems期刊。
2. 摘要
时间序列数据通常是非平稳的,并且会随着时间而演变。即使深度学习在处理顺序数据方面被发现是有效的,深度神经网络在处理训练阶段看不到的情况时的稳定性也很重要。文章基于一种将高阶模糊认知图的学习嵌入深度学习架构的模糊认知块(FCB)来解决这一问题。此后,计算机可以自动对产生观测结果的复杂系统建模,而不是简单地对现有数据进行回归。我们分别设计了一种深度神经网络CNN-FCM,它将现有的卷积网络与FCB相结合。为了验证我们的设计的优势和验证FCB的有效性,文章使用了12个基准数据集,并引入了经典的深度学习架构作为比较。实验结果表明,当前许多流行的深度学习架构在处理偏离训练集的数据时性能下降。在相应的实验中,FCB对CNN-FCM的性能起到了重要的促进作用。结果表明,系统建模可以提高深度学习在时间序列预测中的稳定性。
文章的创新点总结如下:
(1) 文章设计了一种具有良好稳定性的深度神经网络来处理时间序列预测任务。
(2) 文章首次将fcm应用于深度学习,并提高了其在解析时间序列预测中的稳定性。
(3) 文章揭示了系统建模可以促进深度学习在时间序列预测中的稳定性。
(4) CNN-FCM可以看作是一种基于FCM的方法,文章为实现这种方法的端到端训练提供了一种新思路。
3. 模糊认知图(FCB)
一般来说,现实系统通常可以看作是由多个关键组件所构成的网络。对于时间序列数据,可以通过学习潜在变量之间的内在关系从而预测最终的观测结果。为了实现这一目的,一些研究者引入FCM来说明不同潜在变量之间的关系。
假定FCM由Nc个潜在变量构成,对应激活标记为![]() ,潜在变量的关联信息被定义为一个Nc×Nc的矩阵,如下式所示,其中元素值均介于[-1,1]。
,潜在变量的关联信息被定义为一个Nc×Nc的矩阵,如下式所示,其中元素值均介于[-1,1]。
给定激活变量C以及关系矩阵W,下一个时刻的激活值可由下式计算。其中,g(x)表示Sigmoid函数。
上式表示1阶的FCM公式,进一步可以将公式推广至高阶,如下所示。其中,L表示阶数。
现有的基于FCM的时间序列预测方法多由三个阶段组成:(1)利用某些方法从输入中获得分解后的信号。(2)学习前一阶段得到的这些分解信号(潜变量)之间的相关性,预测潜变量在t + 1时的激活状态。(3)根据FCM的输出,利用回归模型预测下一次观测。
4. 模型细节
模糊认知块(Fuzzy cognitive block,FCB):
基于前文对FCM的基本介绍,文章提出了模糊认知块,用于结合深度学习网络学习复杂系统。具体而言,文章首先利用TCN将输入时序数据进行分解,分解元素表示为![]() 作为观测结果的潜变量。基于FCM的计算公式,可以转化为如下公式。
作为观测结果的潜变量。基于FCM的计算公式,可以转化为如下公式。
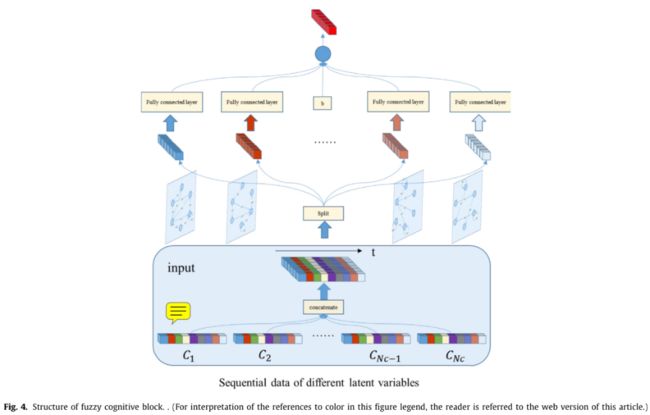
其中表示图对应的邻接矩阵的转置。由上式可知,高阶的FCM本质上是一个可分离的多层网络,每层的邻接矩阵记为Wi。文章通过使用全连接层实现上述计算过程,该结构也成为模糊认知块(FCB),如下图所示。
值得注意的是,在训练过程中,全连接层(Wi)中的参数通过反向传播更新,计算机学习产生观测结果的复杂系统。由于在大多数现实的复杂系统中,Wi趋于稀疏,因此通常将权值衰减项应用于FCM的学习。
结合高阶FCM的卷积神经网络(CNN-FCM):
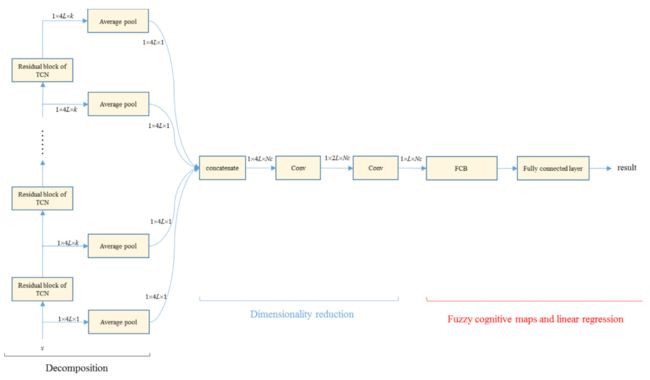
与传统的分解方式不同,文章采用TCN方法提取潜在变量的时间序列数据,而不是将时间序列数据手工分解成一些部分。首先基于TCN提取的序列数据,通过FCB实现高阶FCM的学习。最后,根据FCB的输出,用回归模型预测下一次观测。CNN-FCM的结构如下图所示。
时序数据首先输入至Nc-1个由TCN构成的残差块中,每个残差块的输出被整合并输入至两个卷积层中用于获取Nc个潜变量。进一步,所有潜变量被输入至FCB中用于学习变量间的相互关系。FCM的阶数与输入的数据维度相关,若输入的数据长度为4L,则潜变量的长度为L,并且FCM的阶数也为L。
为充分利用潜变量的激活值,文章利用线性回归对时序数据的未来值进行预测。需要注意的是,由于FCM的激活范围通常在−1到1之间,所以CNN-FCM的残差块使用Leaky-Relu作为激活函数。
该模型的损失函数定义如下。损失函数的前一部分表示真实值和预测值之间的RMSE,后一部分为FCB和回归模型提供了一个权值衰减项,以避免过拟合,该权值衰减项设定为0.0005。
5. 实验
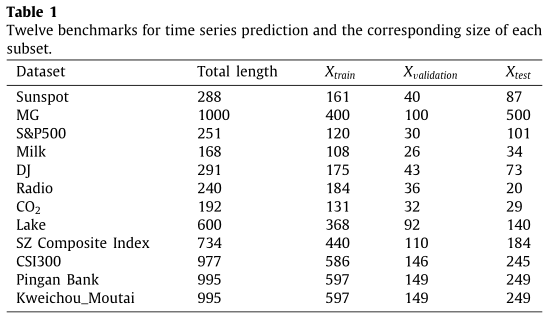
文章使用如下12个数据集用于验证模型的有效性,如下表所示。
文章将CNN-FCM与四种常见的深度学习模型(TCN、LSTM、RNN、GRU)进行比对,并进行了参数灵敏度分析。
与TCN、LSTM、RNN、GRU模型进行比对:
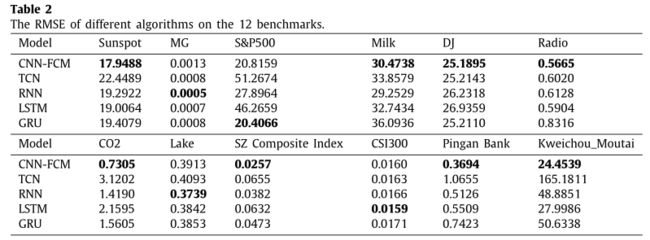
RMSE比对表。
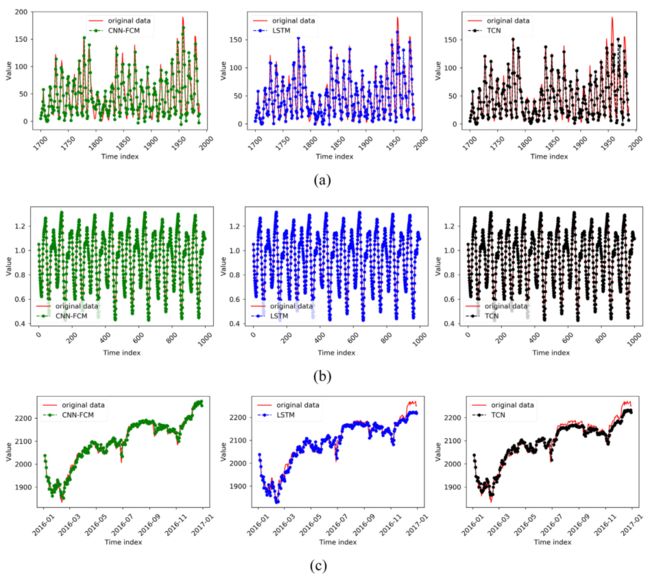
部分预测结果展示。图中(a)、(b)和(c)分别对应数据集中的1-3。
上述12个基准被广泛应用于真实的数据集。为了研究系统建模在促进深度学习稳定性方面的作用,文章利用下式进一步分析了12个基准中的数据不确定性。
不同数据集的不确定性如下表所示。
由RMSE结果比对表可知,CNN-FCM在数据集不确定性的前五个数据集中,其中四个数据集取得了最好的预测效果。
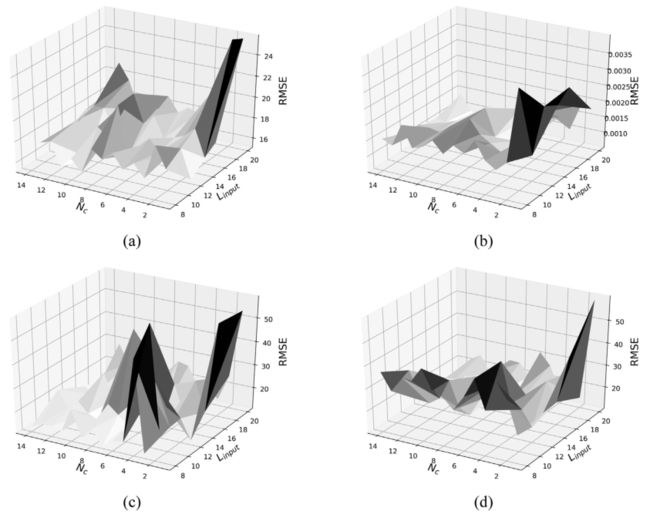
CNN-FCM参数灵敏度分析:
文章分析参数L和Nc对CNN-FCM模型性能的影响。基于上述12个数据集进行实验,下图展示了前四个数据集的实验结果。
6. 总结
深度学习在时间序列预测问题中的应用研究日益突出。目前可用的深度学习架构通常对可用数据进行回归,但忽略了对偏离训练集的数据进行预测的稳定性。由于时间序列数据通常会随着时间的推移而演变,因此相应的模型对这些数据的稳定性是很重要的。
文章提出了一种深度神经网络CNN-FCM,通过集成系统建模来实现对产生观测的复杂系统的学习目的。相对于偏离训练数据集的数据,学习出来的复杂系统能够提供相对更合理的数据处理。这种情况下,可以提高深度学习在时间序列预测中的稳定性。文
章在12个时间序列预测基准上的实验结果验证了我们设计的有效性。该文章是第一篇将FCM应用于深度学习的文章,促进了深度学习在时间序列预测中的稳定性。文章还分析了FCM超参数选择的难点,并将在今后的工作中进一步考虑。
Attention
欢迎关注微信公众号《当交通遇上机器学习》!如果你和我一样是轨道交通、道路交通、城市规划相关领域的,也可以加微信:Dr_JinleiZhang,备注“进群”,加入交通大数据交流群!希望我们共同进步!