目录
- 一元线性回归
-
-
- 1. 确定因变量与自变量之间的关系
-
-
- 1.1 查看变量间有没有相关关系
- 1.2计算相关系数
- 1.3 检验相关系数
- 2.建立模型,并对模型进行估计和检验
-
-
- 2.1 回归模型的拟合
- 2.2 计算回归系数的置信区间
- 2.3 绘制拟合图
- 3.利用回归方程进行预测
-
-
- 3.1 利用回归方程进行预测
- 3.2 绘制置信带和预测带
- 3.3 计算 x0 = 500 时销售收入的点预测值、置信区间和预测区间
- 4. 对回归模型进行诊断
-
-
- 4.1 回归预测值(pre)、残差(res)、标准化残差(zre)
- 4.2 检验线性关系
- 4.3 检验正太性
- 4.4 检验方差齐性
- 4.5 检验独立性
- 数据连接
一元线性回归
- 因变量:研究者特别关注的被预测或被解释的变量,又称为响应变量
- 自变量:用来预测或解释因变量的一个或多个变量,由成为解释变量
- 在回归分析中,只涉及一个自变量时称为【一元回归】,涉及多个自变量时成为【多元回归】
- 如果因变量与自变量之间是线性关系,则称为【线性回归 (linear regression)】
- 如果因变量与自变量之间是非线性关系,则成为【非线性回归 (nonlinear regression)】
一元线性回归建模的大致思路如下:
- 第1步:确定因变量与自变量之间的关系
- 第2步:建立线性关系模型,并对模型进行估计和检验
- 第3步:利用回归方程进行预测
- 第4步:对回归模型进行诊断
1. 确定因变量与自变量之间的关系
1.1 查看变量间有没有相关关系
data = read.csv('***.csv')
library(carData)
library(car)
scatterplot(销售收入~广告支出,data=data,pch=19,xlab="广告支出",ylab="销售收入",cex.lab=0.8)
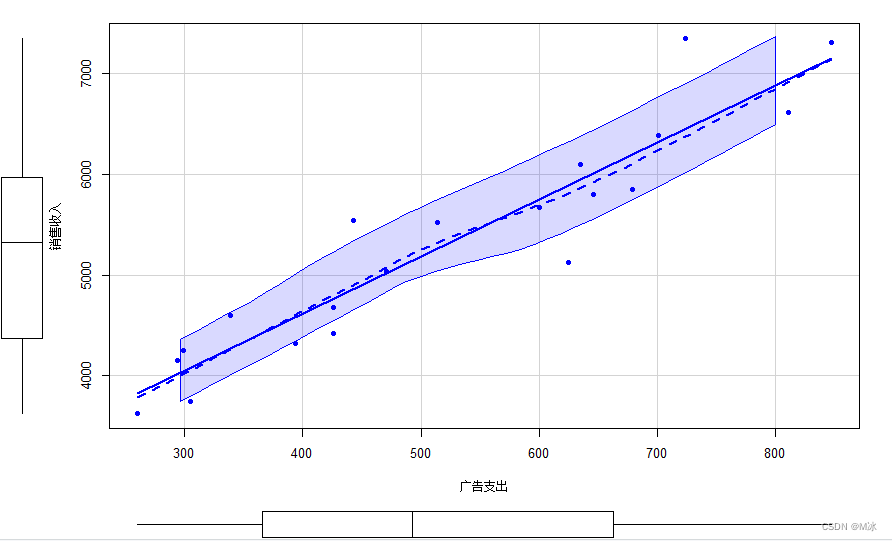
1.2计算相关系数
cor(data$销售收入,data$广告支出)
0.937114
1.3 检验相关系数
cor.test(data$销售收入,data$广告支出)

2.建立模型,并对模型进行估计和检验
2.1 回归模型的拟合
model = lm(销售收入~广告支出,data=data)
summary(model)
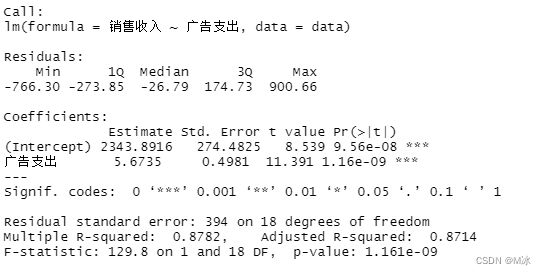
- 模型分析:
- t检验统计量 t =11.391,P = 1.16e-09,P<0.05接近于0,表示广告支出时影响销售收入的一个显著因素。
- 残差标准误(Residual standard error) S_e = 394,表示用广告支出来预测销售收入时平均的预测误差为394万元。
- 决定系数(Multiple R-squared) R^2 = 0.8782 = 87.82%,表示在销售收入取值的总误差中,有87.82%可以由销售收入与广告支出之间的线性关系来解析,模型的拟合程度较高。
- 模型给出的检验统计量(F-statistic) F = 129.8,P = 1.161e-09,P<0.05接近于0,表示销售收入与广告支出之间的线性关系显著。
2.2 计算回归系数的置信区间
confint(model,level = 0.95)

- 根据模型计算出的置信区间表示,广告支出每变动1万元,销售收入的平均改变量在4.627092万~6.719825万元之间。
2.3 绘制拟合图
plot(data$销售收入~data$广告支出)
text(data$销售收入~data$广告支出,labels=data$企业编号,cex=0.6,adj=c(-0.6,0.25),col=4)
abline(model,col=2,lwd=2)
n = nrow(data)
for (i in 1:n){segments(data[i,3],data[i,2],data[i,3],model$fitted[i])}
mtext(expression(hat(y)==2343.8916+5.6735%*%广告支出),cex=0.7,side=1,line=-5,adj=0.6)
arrows(550,4500,550,5350,code=2,angle=15,length=0.1)
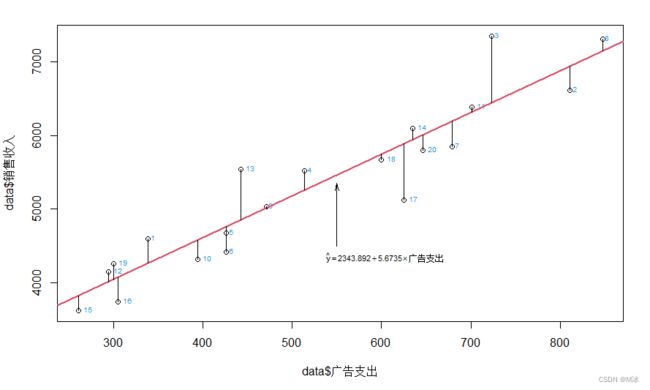
3.利用回归方程进行预测
3.1 利用回归方程进行预测
x0 = data$广告支出
pre_model = predict(model)
con_int = predict(model,data.frame(广告支出=x0),interval="confidence",level=0.95)
pre_int = predict(model,data.frame(广告支出=x0),interval="prediction",level=0.95)
data.frame(销售收入=data$销售收入,点预测值=pre_model,置信下限=con_int[,2],置信上限=con_int[,3],预测下限=pre_int[,2],预测上限=pre_int[,3])

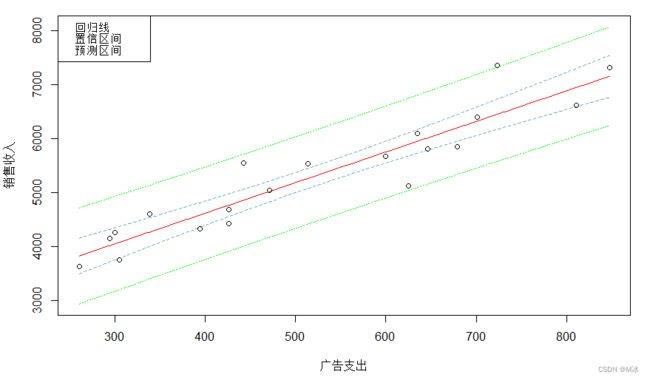
3.2 绘制置信带和预测带
library(investr)
plotFit(model,data=data,interval = "both",level=0.95,col.conf = "skyblue3",col.pred = "green",col.fit = "red2")
legend(x="topleft",legend = c("回归线","置信区间","预测区间"),col=c("red2","skyblue3","green"),cex=0.8)
3.3 计算 x0 = 500 时销售收入的点预测值、置信区间和预测区间
x0 = data.frame(广告支出 = 500)
predict(model,newdata = x0)
5180.621
predict(model,data.frame(广告支出=500),interval="confidence",level=0.95)
fit lwr upr
1 5180.621 4994.127 5367.115
predict(model,data.frame(广告支出=500),interval="prediction",level=0.95)
fit lwr upr
1 5180.621 4332.199 6029.043
4. 对回归模型进行诊断
4.1 回归预测值(pre)、残差(res)、标准化残差(zre)
pre = fitted(model)
res = residuals(model)
zre = model$residuals/(sqrt(deviance(model)/df.residual(model)))
data.frame(销售收入 = data$销售收入,点预测值=pre,残差=res,标准化残差=zre)
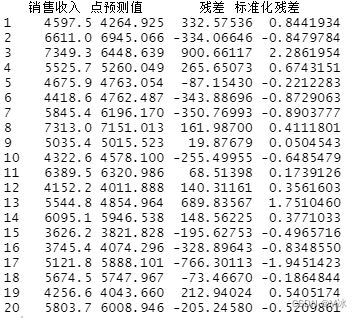
plot(zre)
- 残差图:通过残差图可看出,所有的点基本都以0为中心随机分布在一条水平带
4.2 检验线性关系
library(car)
crPlots(model)

- 从拟合曲线可以看出,销售收入与广告支出之间没有明显的非线性模式,说明二者之间的线性关系假定成立。
- 如果由明显的非线性关系,就需要考虑建立非线性模型
4.3 检验正太性
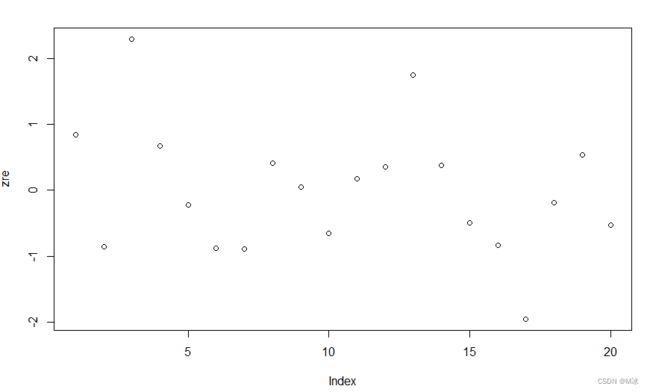
par(mfrow=c(2,2),cex=0.8,cex.main=0.7)
plot(model)
- Normal Q-Q 图:时标准化残差的正态Q-Q,该图可用于检验残差的正太性假定,从该图中可以看出,各个点基本上在直线周围随机分布,没有固定模式,因此,在销售收入与广告支出的线性模型中,关于ε正太性的假定基本成立。
- Residuals vs Fitted 图:残差值与拟合值图,可用于判断因变量与自变量之间的线性关系假定是否成立。如果因变量与自变量之间为线性关系,那么残差值与拟合值之间就没有任何系统关系。从该图可以看出,各残差值基本上在0轴水平线附近随机波动,图中的曲线与残差的0轴水平线没有什么差异,也接近于直线。因此,销售收入与广告支出之间的线性关系成立。
- Scale-Location 图:位置尺图,可用于判断残差的方差齐性假定是否成立。如果ε满足方差齐性,则各个点在水平线周围随机分布。从该图可以看出,在销售收入与广告支出的线性模型中,关于ε方差齐性的假定基本成立。
- Residuals vs Leverage 图:残差与杠杆图,该图可用于鉴别样本数据中是否由离群点,高杠杆值点和强影响点。
4.4 检验方差齐性
ncvTest(model)

spreadLevelPlot(model)
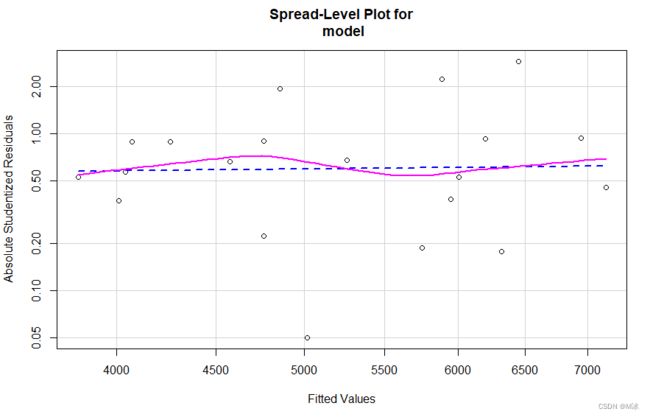
- 检验结论:方差齐性检验的原假设为误差项满足方差齐性,P=0.28854,不拒绝原假设,建立的回归模型满足方差齐性。
4.5 检验独立性
durbinWatsonTest(model)

- 独立性检验结论:该检验的原假设为残差无自相关,P=0.49,不拒绝原假设,显示残差无相关
数据连接










