机器学习 Multivariate Linear Regression——多变量线性回归

完整的数据和代码已经更新至GitHub,欢迎 fork~GitHub链接

Description
In this exercise, you will investigate multivariate linear regression using gradient descent and the normal equations. You will also examine the relationship
between the cost function J(θ), the convergence of gradient descent, and the
learning rate α.

1. 首先读入数据，一共47组数据，其中x为多元变量，一元表示房屋面积，一元表示卧室的数量；y表示房价
2. 将x增加，值为1的一列，即bias
3. 这里需要 preprocess 数据，对数据进行预处理，求出数据的标准差和均值，对数据进行预处理上，来对x进行预处理，将x的值缩放到[-1,1]之间，即一个归一化的操作，让计算更加方便这样便于在后来的梯度下降中，提高效率，而且x更好的收敛（convergence）
4. 实现梯度下降：
   计算出 h(x)的值：
   
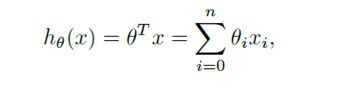
   使用如下BGD 批梯度下降公式：来更新梯度，一次喂入所有数据
   
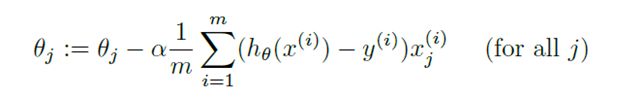
5. 计算损失函数，使用如下的公式：
   
   计算出损失函数，由于x，y都为向量，我们可以将x,y向量化即：
   
   
6. 接下来的问题就是如何确定 学习率了，本次实验也是探讨学习率的变化，对损失函数收敛的影响，而且本次一共迭代50轮，所以，我按照实验要求，将学习率，依次设置为 0.01, 0.03, 0.1, 0.3来看函数收敛的效果，这四根直线的学习率依次为：0.01,0.03,0.1,0.3
   
   下图为当 学习率为0.5时的图像，可见当学习率变大的时候，损失函数下降明显
   
   下图为学习率为 1.5时的图像，损失函数不降反增，发散出去了
   
   可见，学习率，不能过大，过大会导致发散
7. 当学习率为0.4时，参数 theta的值为：
   
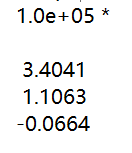
   此时可以预估出 当 x为 1650 square feet and 3 bedrooms时的 y值（房价）为
   
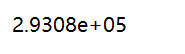
8. 使用另一种方法Normal Equation来计算 theta，这个方法的原理就是使用了最小二乘的方法
   
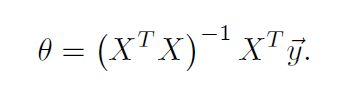
   直接得出线性回归的答案

%加载数据，数据预处理
x=load('F:\Machine Learning\exp\ex2Data\ex2x.dat');
y=load('F:\Machine Learning\exp\ex2Data\ex2y.dat');

m=47;
x=[ones(m,1),x];

sigma=std(x);
mu=mean(x);
x(:,2)=(x(:,2)-mu(2))./sigma(2);
x(:,3)=(x(:,3)-mu(3))./sigma(3);
%数据初始化，定义了四个学习率
theta=zeros(size(x(1,:)))';
theta1=zeros(size(x(1,:)))';
theta2=zeros(size(x(1,:)))';
theta3=zeros(size(x(1,:)))';
alpha=0.01;
alpha1=0.03;
alpha2=0.1;
alpha3=0.3;
J=zeros(50,1);
J1=zeros(50,1);
J2=zeros(50,1);
J3=zeros(50,1);
%函数定义
h=@(x,theta) x*theta;
loss=@(theta,x,y) mean((h(x,theta)-y).^2)/2;
iteration=@(theta,alpha,y,x) theta-alpha*(x'*(h(x,theta)-y))/m;

%开始循环迭代,使用四个学习率上来尝试
for num_iterations=1:50
J(num_iterations)=loss(theta,x,y);
theta=iteration(theta,alpha,y,x);
%第二个
J1(num_iterations)=loss(theta,x,y);
theta1=iteration(theta1,alpha1,y,x);
%第三个
J2(num_iterations)=loss(theta2,x,y);
theta2=iteration(theta2,alpha2,y,x);
%第四个
J3(num_iterations)=loss(theta3,x,y);
theta3=iteration(theta3,alpha3,y,x);
end
figure;
plot(0:49,J(1:50),'b-');
hold on;
plot(0:49,J1(1:50),'r-');
plot(0:49,J2(1:50),'k-');
plot(0:49,J3(1:50),'g-');
xlabel ( 'Number of iterations' );
ylabel ( ' Cost J ' );

theta=zeros(size(x(1,:)))';
alpha=0.4;
J=zeros(50,1);
for num_iterations=1:50
J(num_iterations)=loss(theta,x,y);
theta=iteration(theta,alpha,y,x);
end
plot(0:49,J(1:50),'b-');
xlabel ( 'Number of iterations' );
ylabel ( ' Cost J ' );
disp(theta);
% 数据预处理
t1=(1650-mu(2))./sigma(2);
t2=(3-mu(3))./sigma(3);
disp(h([1,t1,t2],theta));

% 使用 正则方程
u=(x'*x)\x'*y
%u=x\y
disp(u)
t1=(1650-mu(2))./sigma(2);
t2=(3-mu(3))./sigma(3);
disp(h([1,t1,t2],u));