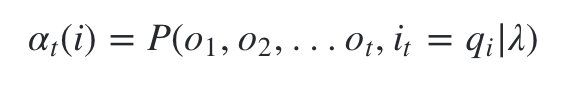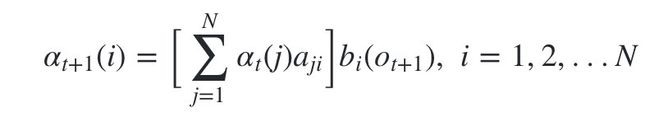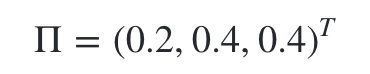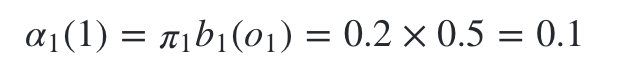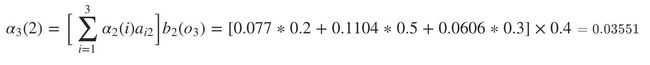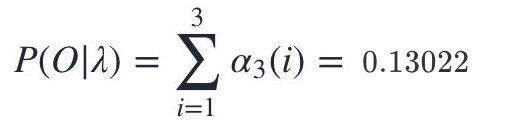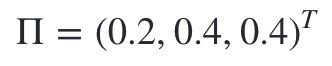机器学习基础 HMM模型(隐马尔科夫)
文章目录
- 一、马尔科夫链
-
- 1. 简介
- 2. 经典举例
- 3. 小结
- 二、HMM简介
-
- 1. 简单案例
- 2. 三个基本问题
- 三、HMM模型基础
-
- 1. 什么样的问题需要HMM模型
- 2. HMM模型的定义
- 3. 一个HMM模型实例
- 4. HMM观测序列的生成
- 5. HMM模型的三个基本问题
- 四、前向后向算法评估观察序列概率
-
- 1. 回顾HMM问题一:求观测序列的概率
- 2. 用前向算法求HMM观测序列的概率
-
- 2.1 流程梳理
- 2.2 算法总结
- 3. HMM前向算法求解实例
- 五、维特比算法解码隐藏状态序列
-
- 1. HMM最可能隐藏状态序列求解概述
- 2. 维特比算法概述
- 3. 维特比算法流程总结
- 4. HMM维特比算法求解实例
- 六、鲍姆-韦尔奇算法简介
-
- 1. 简介
- 2. 鲍姆-韦尔奇算法原理
- 七、HMM模型API介绍
-
- 1. API的安装:
- 2. hmmlearn介绍
- 3. MultinomialHMM实例
推荐参考:https://juejin.cn/post/6844903891834781703
一、马尔科夫链
在机器学习算法中,马尔可夫链(Markov chain)是个很重要的概念。马尔可夫链(Markov chain),又称离散时间马尔可夫链(discrete-time Markov chain),因俄国数学家安德烈·马尔可夫(俄语:Андрей Андреевич Марков)得名。
1. 简介
马尔科夫链即为状态空间中从一个状态到另一个状态转换的随机过程。
-
该过程要求具备“无记忆”的性质:
- 下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性”称作马尔可夫性质。
-
马尔科夫链作为实际过程的统计模型具有许多应用。
-
在马尔可夫链的每一步,系统根据概率分布,可以从一个状态变到另一个状态,也可以保持当前状态。
-
状态的改变叫做转移,与不同的状态改变相关的概率叫做转移概率。
-
既然某一时刻状态转移的概率只依赖前一个状态,那么只要求出系统中任意两个状态之间的转移概率,这个马尔科夫链的模型就定了。
2. 经典举例
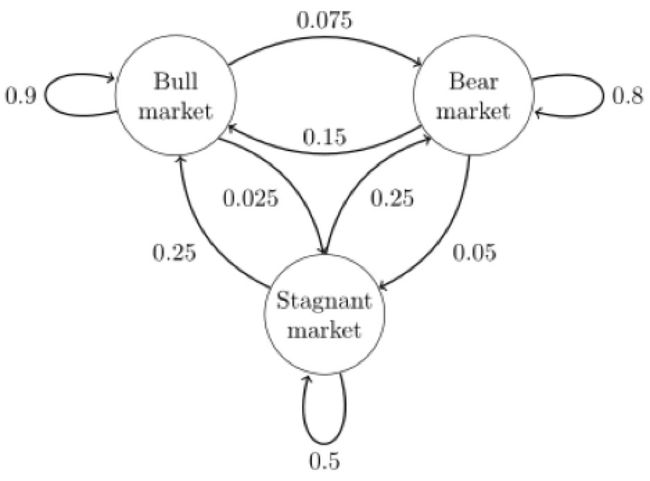
下图中的马尔科夫链是用来表示股市模型,共有三种状态:牛市(Bull market), 熊市(Bear market)和横盘(Stagnant market)。
每一个状态都以一定的概率转化到下一个状态。比如,牛市以0.025的概率转化到横盘的状态。
- 这个状态概率转化图可以以矩阵的形式表示。
- 如果我们定义矩阵阵P某一位置P(i, j)的值为P(j|i),即从状态i变为状态j的概率。
- 另外定义牛市、熊市、横盘的状态分别为0、1、2,这样我们得到了马尔科夫链模型的状态转移矩阵为:
当这个状态转移矩阵P确定以后,整个股市模型就已经确定!
3. 小结
- 马尔科夫链即为
- 状态空间中从一个状态到另一个状态转换的随机过程。
- 该过程要求具备“无记忆”的性质:
- 下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。
二、HMM简介
隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来描述一个含有隐含未知参数的马尔可夫过程。
其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析,例如模式识别。
1. 简单案例
下面我们一起用一个简单的例子来阐述:
- 假设我手里有三个不同的骰子。
- 第一个骰子是我们平常见的骰子(称这个骰子为D6),6个面,每个面(1,2,3,4,5,6)出现的概率是1/6。
- 第二个骰子是个四面体(称这个骰子为D4),每个面(1,2,3,4)出现的概率是1/4。
- 第三个骰子有八个面(称这个骰子为D8),每个面(1,2,3,4,5,6,7,8)出现的概率是1/8。
- 我们开始掷骰子,我们先从三个骰子里挑一个,挑到每一个骰子的概率都是1/3。
- 然后我们掷骰子,得到一个数字,1,2,3,4,5,6,7,8中的一个。不停的重复上述过程,我们会得到一串数字,每个数字都是1,2,3,4,5,6,7,8中的一个。
- 例如我们可能得到这么一串数字(掷骰子10次):1 6 3 5 2 7 3 5 2 4
- 这串数字叫做可见状态链。
但是在隐马尔可夫模型中,我们不仅仅有这么一串可见状态链,还有一串隐含状态链。
- 在这个例子里,这串隐含状态链就是你用的骰子的序列。
- 比如,隐含状态链有可能是:D6 D8 D8 D6 D4 D8 D6 D6 D4 D8
一般来说,HMM中说到的马尔可夫链其实是指隐含状态链,因为隐含状态(骰子)之间存在转换概率(transition probability)。
- 在我们这个例子里,D6的下一个状态是D4,D6,D8的概率都是1/3。D4,D8的下一个状态是D4,D6,D8的转换概率也都一样是1/3。
- 这样设定是为了最开始容易说清楚,但是我们其实是可以随意设定转换概率的。
- 比如,我们可以这样定义,D6后面不能接D4,D6后面是D6的概率是0.9,是D8的概率是0.1。
- 这样就是一个新的HMM。
同样的,尽管可见状态之间没有转换概率,但是隐含状态和可见状态之间有一个概率叫做输出概率(emission probability)。
- 就我们的例子来说,六面骰(D6)产生1的输出概率是1/6。产生2,3,4,5,6的概率也都是1/6。
- 我们同样可以对输出概率进行其他定义。比如,我有一个被赌场动过手脚的六面骰子,掷出来是1的概率更大,是1/2,掷出来是2,3,4,5,6的概率是1/10。
其实对于HMM来说,如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率,做模拟是相当容易的。但是应用HMM模型时候呢,往往是缺失了一部分信息的。
- 有时候你知道骰子有几种,每种骰子是什么,但是不知道掷出来的骰子序列;
- 有时候你只是看到了很多次掷骰子的结果,剩下的什么都不知道。
如果应用算法去估计这些缺失的信息,就成了一个很重要的问题。这些算法我会在后面详细讲。
2. 三个基本问题
- 给定模型,如何有效计算产生观测序列的概率?换言之,如何评估模型与观测序列之间的匹配程度?
- 给定模型和观测序列,如何找到与此观测序列最匹配的状态序列?换言之,如何根据观测序列推断出隐藏的模型状态?
- 给定观测序列,如何调整模型参数使得该序列出现的概率最大?换言之,如何训练模型使其能最好地描述观测数据?
前两个问题是模式识别的问题:1) 根据隐马尔科夫模型得到一个可观察状态序列的概率(评价);2) 找到一个隐藏状态的序列使得这个序列产生一个可观察状态序列的概率最大(解码)。第三个问题就是根据一个可以观察到的状态序列集产生一个隐马尔科夫模型(学习)。
对应的三大问题解法:
- 向前算法(Forward Algorithm)、向后算法(Backward Algorithm)
- 维特比算法(Viterbi Algorithm)
- 鲍姆-韦尔奇算法(Baum-Welch Algorithm) (约等于EM算法)
三、HMM模型基础
1. 什么样的问题需要HMM模型
首先我们来看看什么样的问题解决可以用HMM模型。使用HMM模型时我们的问题一般有这两个特征:
- 1)我们的问题是基于序列的,比如时间序列,或者状态序列。
- 2)我们的问题中有两类数据,
- 一类序列数据是可以观测到的,即观测序列;
- 而另一类数据是不能观察到的,即隐藏状态序列,简称状态序列。
有了这两个特征,那么这个问题一般可以用HMM模型来尝试解决。这样的问题在实际生活中是很多的。
-
比如:我现在给大家写课件,我在键盘上敲出来的一系列字符就是观测序列,而我实际想写的一段话就是隐藏状态序列,输入法的任务就是从敲入的一系列字符尽可能的猜测我要写的一段话,并把最可能的词语放在最前面让我选择,这就可以看做一个HMM模型了。
-
再举一个,假如我上课讲课,我发出的一串连续的声音就是观测序列,而我实际要表达的一段话就是隐藏状态序列,你大脑的任务,就是从这一串连续的声音中判断出我最可能要表达的话的内容。
从这些例子中,我们可以发现,HMM模型可以无处不在。但是上面的描述还不精确,下面我们用精确的数学符号来表述我们的HMM模型。
2. HMM模型的定义
对于HMM模型,首先我们假设Q是所有可能的隐藏状态的集合,V是所有可能的观测状态的集合,即:
- Q = q 1 , q 2 , . . . , q N Q={q_1,q_2,...,q_N} Q=q1,q2,...,qN
- V = v 1 , v 2 , . . . v M V={v_1,v_2,...v_M} V=v1,v2,...vM
其中,N是可能的隐藏状态数,M是所有的可能的观察状态数。
对于一个长度为T的序列,i是对应的状态序列, O是对应的观察序列,即:
- i = i 1 , i 2 , . . . , i T i={i_1,i_2,...,i_T} i=i1,i2,...,iT
- O = o 1 , o 2 , . . . o T O={o_1,o_2,...o_T} O=o1,o2,...oT
其中,任意一个隐藏状态 i t ∈ Q i_t \in Q it∈Q, 任意一个观察状态 o t ∈ V o_t\in V ot∈V
HMM模型做了两个很重要的假设如下:
1) 齐次马尔科夫链假设。
-
即任意时刻的隐藏状态只依赖于它前一个隐藏状态。
-
当然这样假设有点极端,因为很多时候我们的某一个隐藏状态不仅仅只依赖于前一个隐藏状态,可能是前两个或者是前三个。
-
但是这样假设的好处就是模型简单,便于求解。
-
如果在时刻t的隐藏状态是 i t = q i i_t=q_i it=qi,在时刻 t + 1 t+1 t+1的隐藏状态是 i t + 1 = q j i_{t+1}=q_j it+1=qj, 则从时刻t到时刻t+1的HMM状态转移概率 a i j a_{ij} aij可以表示为:
- a i j = P ( i t + 1 = q j ∣ i t = q i ) a_{ij}=P(i_{t+1}= q_j | i_t=q_i) aij=P(it+1=qj∣it=qi)
-
这样 a i j a_{ij} aij 可以组成马尔科夫链的状态转移矩阵A:
- A = [ a i j ] N × N A=[a_{ij}]_{N \times N} A=[aij]N×N
- A = [ a i j ] N × N A=[a_{ij}]_{N \times N} A=[aij]N×N
2) 观测独立性假设。
-
即任意时刻的观察状态只仅仅依赖于当前时刻的隐藏状态,这也是一个为了简化模型的假设。
-
如果在时刻t的隐藏状态是 i t = q j i_t=q_j it=qj , 而对应的观察状态为 o t = v k o_t=v_k ot=vk , 则该时刻观察状态 v k v_k vk 在隐藏状态 q j q_j qj 下生成的概率为 b j ( k ) b_j(k) bj(k),满足:
- b j ( k ) = P ( o t = v k ∣ i t = q j ) b_j(k)=P(o_t=v_k|i_t=q_j) bj(k)=P(ot=vk∣it=qj)
-
这样 b j ( k ) b_j(k) bj(k)可以组成观测状态生成的概率矩阵B:
- B = [ b j ( k ) ] N × M B=[b_j(k)]_{N \times M} B=[bj(k)]N×M
- B = [ b j ( k ) ] N × M B=[b_j(k)]_{N \times M} B=[bj(k)]N×M
-
除此之外,我们需要一组在时刻t=1的隐藏状态概率分布 Π \Pi Π :
- Π = [ Π i ] N \Pi =[\Pi_i]_N Π=[Πi]N
-
其中 Π i = P ( i 1 = q i ) \Pi _i=P(i_1=q_i) Πi=P(i1=qi)
-
一个HMM模型,可以由隐藏状态初始概率分布 Π \Pi Π , 状态转移概率矩阵A和观测状态概率矩阵B决定。
Π \Pi Π ,A决定状态序列,B决定观测序列。
因此,HMM模型可以由一个三元组 λ \lambda λ 表示如下:
- λ = ( A , B , Π ) = \lambda =(A,B, \Pi )= λ=(A,B,Π)=(状态序列,观测序列,初始状态概率分布)
3. 一个HMM模型实例
下面我们用一个简单的实例来描述上面抽象出的HMM模型。这是一个盒子与球的模型。
例子来源于李航的《统计学习方法》。
假设我们有3个盒子,每个盒子里都有红色和白色两种球,这三个盒子里球的数量分别是:

按照下面的方法从盒子里抽球,开始的时候,
- 从第一个盒子抽球的概率是0.2,
- 从第二个盒子抽球的概率是0.4,
- 从第三个盒子抽球的概率是0.4。
以这个概率抽一次球后,将球放回。
然后从当前盒子转移到下一个盒子进行抽球。规则是:
- 如果当前抽球的盒子是第一个盒子,则以0.5的概率仍然留在第一个盒子继续抽球,以0.2的概率去第二个盒子抽球,以0.3的概率去第三个盒子抽球。
- 如果当前抽球的盒子是第二个盒子,则以0.5的概率仍然留在第二个盒子继续抽球,以0.3的概率去第一个盒子抽球,以0.2的概率去第三个盒子抽球。
- 如果当前抽球的盒子是第三个盒子,则以0.5的概率仍然留在第三个盒子继续抽球,以0.2的概率去第一个盒子抽球,以0.3的概率去第二个盒子抽球。
如此下去,直到重复三次,得到一个球的颜色的观测序列:
- O={红,白,红}
注意在这个过程中,观察者只能看到球的颜色序列,却不能看到球是从哪个盒子里取出的。
那么按照我们前面HMM模型的定义,我们的观察状态集合是:
- V={红,白},M=2
我们的隐藏状态集合是:
- Q={盒子1,盒子2,盒子3},N=3
而观察序列和状态序列的长度为3.
初始状态分布 Π \Pi Π为:
- Π = ( 0.2 , 0.4 , 0.4 ) T \Pi=(0.2,0.4,0.4)^T Π=(0.2,0.4,0.4)T
状态转移概率分布A矩阵为:
观测状态概率B矩阵为:
4. HMM观测序列的生成
从上面的例子,我们也可以抽象出HMM观测序列生成的过程。
-
输入的是HMM的模型 λ = ( A , B , Π ) \lambda =(A,B,\Pi ) λ=(A,B,Π),观测序列的长度 T T T
-
输出是观测序列 O = o 1 , o 2 , . . . o T O={o_1,o_2,...o_T} O=o1,o2,...oT
生成的过程如下:
-
1)根据初始状态概率分布\PiΠ生成隐藏状态 i 1 i_1 i1
-
2)for t from 1 to T
- a. 按照隐藏状态 i t i_t it的观测状态分布 b i t ( k ) b_{it}(k) bit(k)生成观察状态 o t o_t ot
- b. 按照隐藏状态 i t i_t it 的状态转移概率分布 a i t , i t + 1 ai_t, i_{t+1} ait,it+1产生隐藏状态 i t + 1 i_{t+1} it+1
所有的 o t o_t ot 一起形成观测序列 O = o 1 , o 2 , . . . o T O={o_1,o_2,...o_T} O=o1,o2,...oT
5. HMM模型的三个基本问题
HMM模型一共有三个经典的问题需要解决:
1)评估观察序列概率 —— 前向后向的概率计算
- 即给定模型 λ = ( A , B , Π ) \lambda =(A,B,\Pi ) λ=(A,B,Π)和观测序列 O = { o 1 , o 2 , . . . o T } O=\{o_1,o_2,...o_T\} O={o1,o2,...oT},计算在模型 λ \lambda λ 下某一个观测序列O出现的概率P(O| λ \lambda λ )。
- 这个问题的求解需要用到前向后向算法,是HMM模型三个问题中最简单的。
2)预测问题,也称为解码问题 ——维特比(Viterbi)算法
- 即给定模型 λ = ( A , B , Π ) \lambda =(A,B,\Pi ) λ=(A,B,Π)和观测序列 O = { o 1 , o 2 , . . . o T } O=\{o_1,o_2,...o_T\} O={o1,o2,...oT},求给定观测序列条件下,最可能出现的对应的状态序列。
- 这个问题的求解需要用到基于动态规划的维特比算法,是HMM模型三个问题中复杂度居中的算法。
3)模型参数学习问题 —— 鲍姆-韦尔奇(Baum-Welch)算法(状态未知) ,这是一个学习问题
- 即给定观测序列 O = { o 1 , o 2 , . . . o T } O=\{o_1,o_2,...o_T\} O={o1,o2,...oT},估计模型 λ = ( A , B , Π ) \lambda =(A,B,\Pi ) λ=(A,B,Π)的参数,使该模型下观测序列的条件概率 P ( O ∣ λ ) P(O|\lambda ) P(O∣λ)最大。
- 这个问题的求解需要用到基于EM算法的鲍姆-韦尔奇算法,是HMM模型三个问题中最复杂的。
接下来的三节,我们将基于这个三个问题展开讨论。
四、前向后向算法评估观察序列概率
本节我们就关注HMM第一个基本问题的解决方法,即已知模型和观测序列,求观测序列出现的概率。
1. 回顾HMM问题一:求观测序列的概率
首先我们回顾下HMM模型的问题一。这个问题是这样的。
我们已知HMM模型的参数 λ = ( A , B , Π ) \lambda =(A,B,\Pi) λ=(A,B,Π)。
其中A是隐藏状态转移概率的矩阵,
B是观测状态生成概率的矩阵,
Π \Pi Π 是隐藏状态的初始概率分布。
同时我们也已经得到了观测序列 O = { o 1 , o 2 , . . . o T } O=\{o_1,o_2,...o_T\} O={o1,o2,...oT},
现在我们要求观测序列O在模型 λ \lambda λ 下出现的条件概率 P ( O ∣ λ ) P(O|\lambda ) P(O∣λ)。
乍一看,这个问题很简单。因为我们知道所有的隐藏状态之间的转移概率和所有从隐藏状态到观测状态生成概率,那么我们是可以暴力求解的。
我们可以列举出所有可能出现的长度为T的隐藏序列 i = { i 1 , i 2 , . . . , i T } i=\{i_1,i_2,...,i_T\} i={i1,i2,...,iT},分别求出这些隐藏序列与观测序列 O = { o 1 , o 2 , . . . o T } O=\{o_1,o_2,...o_T\} O={o1,o2,...oT}的联合概率分布 P ( O , i ∣ λ ) P(O,i|\lambda ) P(O,i∣λ),这样我们就可以很容易的求出边缘分布 P ( O ∣ λ ) P(O|\lambda ) P(O∣λ)了。
具体暴力求解的方法是这样的:
-
首先,任意隐藏序列 i = i 1 , i 2 , . . . , i T i={i_1,i_2,...,i_T} i=i1,i2,...,iT出现的概率是:
- P ( i ∣ λ ) = Π i 1 a i 1 , i 2 a i 2 , i 3 . . . a i T − 1 , i T P(i|\lambda )=\Pi _{i1}a_{i1,i2}a_{i2,i3}...a_{iT-1,iT} P(i∣λ)=Πi1ai1,i2ai2,i3...aiT−1,iT
- P ( i ∣ λ ) = Π i 1 a i 1 , i 2 a i 2 , i 3 . . . a i T − 1 , i T P(i|\lambda )=\Pi _{i1}a_{i1,i2}a_{i2,i3}...a_{iT-1,iT} P(i∣λ)=Πi1ai1,i2ai2,i3...aiT−1,iT
-
对于固定的状态序列 i = i 1 , i 2 , . . . , i T i={i_1,i_2,...,i_T} i=i1,i2,...,iT ,我们要求的观察序列 O = o 1 , o 2 , . . . o T O={o_1,o_2,...o_T} O=o1,o2,...oT 出现的概率是:
- P ( O ∣ i , λ ) = b i 1 ( o 1 ) b i 2 ( o 2 ) . . . b i T ( o T ) P(O|i,\lambda )=b_{i1}(o_1)b_{i2}(o_2)...b_{iT}(o_T) P(O∣i,λ)=bi1(o1)bi2(o2)...biT(oT)
-
然后求边缘概率分布,即可得到观测序列O在模型 λ \lambda λ 下出现的条件概率P(O| λ \lambda λ ):

虽然上述方法有效,但是如果我们的隐藏状态数N非常多的那就麻烦了,此时我们预测状态有 N T N^T NT种组合,算法的时间复杂度是 O ( T N T ) O(TN^T) O(TNT)阶的。
因此对于一些隐藏状态数极少的模型,我们可以用暴力求解法来得到观测序列出现的概率,但是如果隐藏状态多,则上述算法太耗时,我们需要寻找其他简洁的算法。
前向后向算法就是来帮助我们在较低的时间复杂度情况下求解这个问题的。
2. 用前向算法求HMM观测序列的概率
前向后向算法是前向算法和后向算法的统称,这两个算法都可以用来求HMM观测序列的概率。我们先来看看前向算法是如何求解这个问题的。
2.1 流程梳理
前向算法本质上属于动态规划的算法,也就是我们要通过找到局部状态递推的公式,这样一步步的从子问题的最优解拓展到整个问题的最优解。
-
在前向算法中,通过定义“前向概率”来定义动态规划的这个局部状态。
-
什么是前向概率呢, 其实定义很简单:定义时刻t时隐藏状态为 q i q_i qi, 观测状态的序列为 o 1 , o 2 , . . . o t o_1,o_2,...o_t o1,o2,...ot的概率为前向概率。记为:
-
既然是动态规划,我们就要递推了,现在假设我们已经找到了在时刻t时各个隐藏状态的前向概率,现在我们需要递推出时刻t+1时各个隐藏状态的前向概率。
-
我们可以基于时刻t时各个隐藏状态的前向概率,再乘以对应的状态转移概率,即 α t ( j ) a j i \alpha _t(j)a_{ji} αt(j)aji 就是在时刻t观测到 o 1 , o 2 , . . . o t o_1,o_2,...o_t o1,o2,...ot,并且时刻t隐藏状态 q j q_j qj , 时刻t+1隐藏状态 q i q_i qi的概率。
-
如果将下面所有的线对应的概率求和,即 ∑ j = 1 N α ( j ) α j i \sum_{j=1}^{N}\alpha(j)\alpha_{ji} ∑j=1Nα(j)αji就是在时刻t观测到 o 1 , o 2 , . . . o t o_1,o_2,...o_t o1,o2,...ot ,并且时刻t+1隐藏状态 q i q_i qi 的概率。
-
继续一步,由于观测状态 o t + 1 o_{t+1} ot+1 只依赖于t+1时刻隐藏状态 q i q_i qi, 这样
 就是在时刻t+1观测到 o 1 , o 2 , . . . o t , o t + 1 o_1,o_2,...o_t,o_{t+1} o1,o2,...ot,ot+1 ,并且时刻t+1隐藏状态 q i q_i qi 的概率。
就是在时刻t+1观测到 o 1 , o 2 , . . . o t , o t + 1 o_1,o_2,...o_t,o_{t+1} o1,o2,...ot,ot+1 ,并且时刻t+1隐藏状态 q i q_i qi 的概率。
我们的动态规划从时刻1开始,到时刻T结束,由于 α T ( i ) \alpha _T(i) αT(i)表示在时刻T观测序列为 o 1 , o 2 , . . . o T o_1,o_2,...o_T o1,o2,...oT ,并且时刻T隐藏状态 q i q_i qi的概率,我们只要将所有隐藏状态对应的概率相加,即 ∑ i = 1 N α T ( i ) \sum_{i=1}^{N}\alpha_T(i) ∑i=1NαT(i)就得到了在时刻T观测序列为 o 1 , o 2 , . . . o t o_1,o_2,...o_t o1,o2,...ot的概率。
2.2 算法总结
-
输入:HMM模型 λ = ( A , B , Π ) \lambda =(A,B,\Pi ) λ=(A,B,Π),观测序列 O = ( o 1 , o 2 , . . . o T ) O=(o_1,o_2,...o_T) O=(o1,o2,...oT)
-
输出:观测序列概率 P ( O ∣ λ ) P(O|\lambda ) P(O∣λ)
从递推公式可以看出,我们的算法时间复杂度是 O ( T N 2 ) O(TN^2) O(TN2),比暴力解法的时间复杂度 O ( T N T ) O(TN^T) O(TNT)少了几个数量级。
3. HMM前向算法求解实例
这里我们用前面盒子与球的例子来显示前向概率的计算。 我们的观察集合是:
我们的状态集合是:
而观察序列和状态序列的长度为3.
初始状态分布为:
状态转移概率分布矩阵为:
观测状态概率矩阵为:
球的颜色的观测序列:
按照我们上一节的前向算法。首先计算时刻1三个状态的前向概率:
时刻1是红色球,
现在我们可以开始递推了,首先递推时刻2三个状态的前向概率:
时刻2是白色球,
继续递推,现在我们递推时刻3三个状态的前向概率:
时刻3是红色球,
最终我们求出观测序列:O=红,白,红的概率为:
向后算法原理大概一致,可自行查询
五、维特比算法解码隐藏状态序列
学习目标
知道维特比算法解码隐藏状态序列
在本篇我们会讨论维特比算法解码隐藏状态序列,即给定模型和观测序列,求给定观测序列条件下,最可能出现的对应的隐藏状态序列。
HMM模型的解码问题最常用的算法是维特比算法,当然也有其他的算法可以求解这个问题。
同时维特比算法是一个通用的求序列最短路径的动态规划算法,也可以用于很多其他问题。
1. HMM最可能隐藏状态序列求解概述
HMM模型的解码问题即:
- 给定模型 λ = ( A , B , Π ) \lambda=(A,B,\Pi) λ=(A,B,Π)和观测序列 O = o 1 , o 2 , . . . o T O={o_1,o_2,...o_T} O=o1,o2,...oT,求给定观测序列O条件下,最可能出现的对应的状态序列 I ∗ = i 1 ∗ , i 2 ∗ , . . . i T ∗ I^\ast ={i^\ast _1,i^\ast _2,...i^\ast _T} I∗=i1∗,i2∗,...iT∗ ,即 P ( I ∗ ∣ O ) P(I^\ast |O) P(I∗∣O)的最大化。
一个可能的近似解法是求出观测序列O在每个时刻t最可能的隐藏状态 i t ∗ i^\ast _t it∗ 然后得到一个近似的隐藏状态序列 I ∗ = i 1 ∗ , i 2 ∗ , . . . i T ∗ I^\ast ={i^\ast _1,i^\ast _2,...i^\ast _T} I∗=i1∗,i2∗,...iT∗I。要这样近似求解不难,利用前向后向算法评估观察序列概率的定义:
- 在给定模型 λ \lambda λ和观测序列O时,在时刻t处于状态 q i q_i qi 的概率是 γ t ( i ) \gamma _t(i) γt(i),这个概率可以通过HMM的前向算法与后向算法计算。这样我们有:

近似算法很简单,但是却不能保证预测的状态序列整体是最可能的状态序列,因为预测的状态序列中某些相邻的隐藏状态可能存在转移概率为0的情况。
而维特比算法可以将HMM的状态序列作为一个整体来考虑,避免近似算法的问题,下面我们来看看维特比算法进行HMM解码的方法。
2. 维特比算法概述
维特比算法是一个通用的解码算法,是基于动态规划的求序列最短路径的方法。
既然是动态规划算法,那么就需要找到合适的局部状态,以及局部状态的递推公式。在HMM中,维特比算法定义了两个局部状态用于递推。
1)第一个局部状态是在时刻t隐藏状态为 i i i所有可能的状态转移路径 i 1 , i 2 , . . . i t i_1,i_2,...i_t i1,i2,...it 中的概率最大值。
由 δ t ( i ) \delta _t(i) δt(i)的定义可以得到 δ \delta δ的递推表达式:
2)第二个局部状态由第一个局部状态递推得到。
- 我们定义在时刻t隐藏状态为i的所有单个状态转移路径 ( i 1 , i 2 , . . . , i t − 1 , i ) (i_1,i_2,...,i_{t-1},i) (i1,i2,...,it−1,i)中概率最大的转移路径中第t-1个节点的隐藏状态为 ψ t ( i ) \psi _t(i) ψt(i),
- 其递推表达式可以表示为:
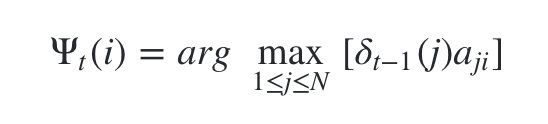
有了这两个局部状态,我们就可以从时刻0一直递推到时刻T,然后利用 ψ t ( i ) \psi _t(i) ψt(i)记录的前一个最可能的状态节点回溯,直到找到最优的隐藏状态序列。
3. 维特比算法流程总结
现在我们来总结下维特比算法的流程:
-
输入:HMM模型 λ = ( A , B , Π ) \lambda=(A,B,\Pi) λ=(A,B,Π),观测序列 O = ( o 1 , o 2 , . . . o T ) O=(o_1,o_2,...o_T) O=(o1,o2,...oT)
-
输出:最有可能的隐藏状态序列 I ∗ = i 1 ∗ , i 2 ∗ , . . . i T ∗ I^\ast ={i^\ast _1,i^\ast _2,...i^\ast _T} I∗=i1∗,i2∗,...iT∗
流程如下:
-
2)进行动态规划递推时刻 t = 2 , 3 , . . . T t=2,3,...T t=2,3,...T时刻的局部状态:
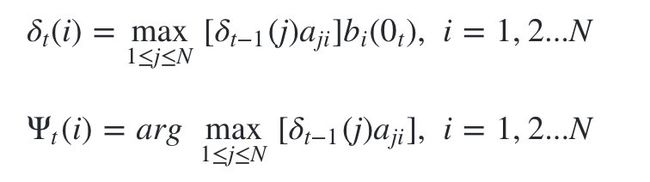
-
3)计算时刻T最大的 δ T ( i ) \delta _T(i) δT(i),即为最可能隐藏状态序列出现的概率。计算时刻T最大的 ψ t ( i ) \psi _t(i) ψt(i),即为时刻T最可能的隐藏状态。
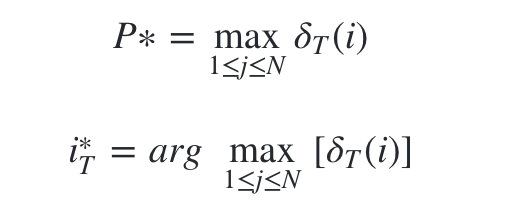
-
4)利用局部状态 ψ t ( i ) \psi _t(i) ψt(i)开始回溯。对于 t = T − 1 , T − 2 , . . . , 1 t=T-1,T-2,...,1 t=T−1,T−2,...,1:
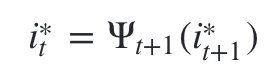
最终得到最有可能的隐藏状态序列 I ∗ = i 1 ∗ , i 2 ∗ , . . . i T ∗ I^\ast ={i^\ast _1,i^\ast _2,...i^\ast _T} I∗=i1∗,i2∗,...iT∗
4. HMM维特比算法求解实例
下面我们仍然用盒子与球的例子来看看HMM维特比算法求解。 我们的观察集合是:
我们的状态集合是:
而观察序列和状态序列的长度为3.
初始状态分布为:
状态转移概率分布矩阵为:
观测状态概率矩阵为:
球的颜色的观测序列:
按照我们前面的维特比算法,首先需要得到三个隐藏状态在时刻1时对应的各自两个局部状态,此时观测状态为1:
现在开始递推三个隐藏状态在时刻2时对应的各自两个局部状态,此时观测状态为2:
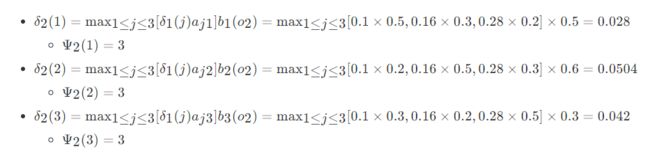
继续递推三个隐藏状态在时刻3时对应的各自两个局部状态,此时观测状态为1:

此时已经到最后的时刻,我们开始准备回溯。此时最大概率为 δ 3 ( 3 ) \delta _3(3) δ3(3),从而得到 i 3 ∗ = 3 i^\ast _3=3 i3∗=3
由于 ψ 3 ( 3 ) = 3 \psi _3(3)=3 ψ3(3)=3,所以 i 2 ∗ = 3 i^\ast _2=3 i2∗=3 , 而又由于 ψ 2 ( 3 ) = 3 \psi _2(3)=3 ψ2(3)=3,所以 i 1 ∗ = 3 i^\ast _1=3 i1∗=3。从而得到最终的最可能的隐藏状态序列为:(3,3,3)。
六、鲍姆-韦尔奇算法简介
1. 简介
模型参数学习问题 —— 鲍姆-韦尔奇(Baum-Welch)算法(状态未知) ,
- 即给定观测序列 O = { o 1 , o 2 , . . . o T } O=\{o_1,o_2,...o_T\} O={o1,o2,...oT},估计模型 λ = ( A , B , Π ) \lambda =(A,B,\Pi ) λ=(A,B,Π)的参数,使该模型下观测序列的条件概率 P ( O ∣ λ ) P(O|\lambda ) P(O∣λ)最大。
- 它的解法最常用的是鲍姆-韦尔奇算法,其实就是基于EM算法的求解,只不过鲍姆-韦尔奇算法出现的时代,EM算法还没有被抽象出来,所以被叫为鲍姆-韦尔奇算法。
2. 鲍姆-韦尔奇算法原理
鲍姆-韦尔奇算法原理既然使用的就是EM算法的原理,
- 那么我们需要在E步求出联合分布 P ( O , I ∣ λ ) P(O,I|\lambda) P(O,I∣λ)基于条件概率 P ( I ∣ O , λ ‾ ) P(I|O,\overline{\lambda}) P(I∣O,λ)的期望,其中 λ ‾ \overline{\lambda} λ为当前的模型参数,
- 然后在M步最大化这个期望,得到更新的模型参数 λ \lambda λ。
接着不停的进行EM迭代,直到模型参数的值收敛为止。
首先来看看E步,当前模型参数为 λ ‾ \overline{\lambda} λ, 联合分布 P ( O , I ∣ λ ) P(O,I|\lambda) P(O,I∣λ)基于条件概率 P ( I ∣ O , λ ‾ ) P(I|O,\overline{\lambda}) P(I∣O,λ)的期望表达式为:
- L ( λ , λ ‾ ) = ∑ I P ( I ∣ O , λ ‾ ) l o g P ( O , I ∣ λ ) L(\lambda, \overline{\lambda}) = \sum\limits_{I}P(I|O,\overline{\lambda})logP(O,I|\lambda) L(λ,λ)=I∑P(I∣O,λ)logP(O,I∣λ)
在M步,我们极大化上式,然后得到更新后的模型参数如下:
- λ ‾ = a r g max λ ∑ I P ( I ∣ O , λ ‾ ) l o g P ( O , I ∣ λ ) \overline{\lambda} = arg\;\max_{\lambda}\sum\limits_{I}P(I|O,\overline{\lambda})logP(O,I|\lambda) λ=argmaxλI∑P(I∣O,λ)logP(O,I∣λ)
通过不断的E步和M步的迭代,直到 λ ‾ \overline{\lambda} λ收敛。
七、HMM模型API介绍
1. API的安装:
官网链接:https://hmmlearn.readthedocs.io/en/latest/
pip3 install hmmlearn
2. hmmlearn介绍
hmmlearn实现了三种HMM模型类,按照观测状态是连续状态还是离散状态,可以分为两类。
GaussianHMM和GMMHMM是连续观测状态的HMM模型,而MultinomialHMM是离散观测状态的模型,也是我们在HMM原理系列篇里面使用的模型。
在这里主要介绍我们前面一直讲的关于离散状态的MultinomialHMM模型。
对于MultinomialHMM的模型,使用比较简单,里面有几个常用的参数:
- "startprob_"参数对应我们的隐藏状态初始分布\PiΠ,
- "transmat_"对应我们的状态转移矩阵A,
- "emissionprob_"对应我们的观测状态概率矩阵B。
3. MultinomialHMM实例
下面我们用我们在前面讲的关于球的那个例子使用MultinomialHMM跑一遍。
import numpy as np
from hmmlearn import hmm
# 设定隐藏状态的集合
states = ["box 1", "box 2", "box3"]
n_states = len(states)
# 设定观察状态的集合
observations = ["red", "white"]
n_observations = len(observations)
# 设定初始状态分布
start_probability = np.array([0.2, 0.4, 0.4])
# 设定状态转移概率分布矩阵
transition_probability = np.array([
[0.5, 0.2, 0.3],
[0.3, 0.5, 0.2],
[0.2, 0.3, 0.5]
])
# 设定观测状态概率矩阵
emission_probability = np.array([
[0.5, 0.5],
[0.4, 0.6],
[0.7, 0.3]
])
# 设定模型参数
model = hmm.MultinomialHMM(n_components=n_states)
model.startprob_=start_probability # 初始状态分布
model.transmat_=transition_probability # 状态转移概率分布矩阵
model.emissionprob_=emission_probability # 观测状态概率矩阵
现在我们来跑一跑HMM问题三维特比算法的解码过程,使用和之前一样的观测序列来解码,代码如下:
seen = np.array([[0,1,0]]).T # 设定观测序列
box = model.predict(seen)
print("球的观测顺序为:\n", ", ".join(map(lambda x: observations[x], seen.flatten())))
# 注意:需要使用flatten方法,把seen从二维变成一维
print("最可能的隐藏状态序列为:\n", ", ".join(map(lambda x: states[x], box)))
我们再来看看求HMM问题一的观测序列的概率的问题,代码如下:
print(model.score(seen))
# 输出结果是:-2.03854530992
要注意的是score函数返回的是以自然对数为底的对数概率值,我们在HMM问题一中手动计算的结果是未取对数的原始概率是0.13022。对比一下:
import math
math.exp(-2.038545309915233)
# ln0.13022≈−2.0385
# 输出结果是:0.13021800000000003