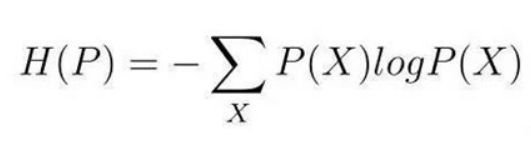HMM(隐马尔可夫模型)
原文:
https://www.cnblogs.com/skyme/p/4651331.html
https://blog.csdn.net/SummerHmh/article/details/93165974
笔记:
一、熵(Entropy)
熵是表示物质系统状态的一种度量,用它表征系统的无序程度。熵越大,系统越无序,意味着系统结构和运动的不确定和无规则;反之,熵越小,系统越有序,意味着具有确定和有规则的运动状态。熵的中文意思是热量被温度除的商。负熵是物质系统有序化,组织化,复杂化状态的一种度量。
二、最大熵模型
这个“熵“并不是指热力学上熵的概念,而是由信息论男神克劳德·艾尔伍德·香农(Claude Elwood Shannon)在1948年提出的“信息熵“,用来描述信息的不确定程度。
信息熵公式:
最大熵原理是一种选择随机变量统计特性最符合客观情况的准则,也称为最大信息原理。随机量的概率分布是很难测定的,一般只能测得其各种均值(如数学期望、方差等)或已知某些限定条件下的值(如峰值、取值个数等),符合测得这些值的分布可有多种、以至无穷多种,通常,其中有一种分布的熵最大。选用这种具有最大熵的分布作为该随机变量的分布,是一种有效的处理方法和准则。这种方法虽有一定的主观性,但可以认为是最符合客观情况的一种选择。
参考:图解最大熵原理 https://blog.csdn.net/yangziluomu/article/details/81986271
匈牙利著名数学家、信息论最高奖香农奖得主希萨(Csiszar)证明,对任何一组不自相矛盾的信息,这个最大熵模型不仅存在,而且是唯一的。而且它们都有同一个非常简单的形式 -- 指数函数。
三、HMM(隐马尔可夫模型)
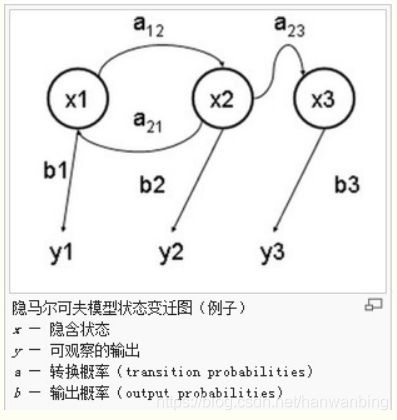
隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析,例如模式识别。
是在被建模的系统被认为是一个马尔可夫过程与未观测到的(隐藏的)的状态的统计马尔可夫模型。
在隐马尔可夫模型中,我们不仅仅有这么一串可见状态链,还有一串隐含状态链。一般来说,HMM中说到的马尔可夫链其实是指隐含状态链,因为隐含状态(骰子)之间存在转换概率(transition probability)。
其实对于HMM来说,如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率,做模拟是相当容易的。但是应用HMM模型时候呢,往往是缺失了一部分信息的,有时候你知道骰子有几种,每种骰子是什么,但是不知道掷出来的骰子序列;有时候你只是看到了很多次掷骰子的结果,剩下的什么都不知道。如果应用算法去估计这些缺失的信息,就成了一个很重要的问题。
和HMM模型相关的算法主要分为三类,分别解决三种问题:
1)知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道每次掷出来的都是哪种骰子(隐含状态链)。
a.穷举法
b.Viterbi algorithm维特比算法
2)还是知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道掷出这个结果的概率。
a.穷举法
b.前向算法(forward algorithm)
3)知道骰子有几种(隐含状态数量),不知道每种骰子是什么(转换概率),观测到很多次掷骰子的结果(可见状态链),我想反推出每种骰子是什么(转换概率)。(最常见的情况)
通常用维特比算法Viterbi algorithm解决。维特比算法就是求解HMM上的最短路径(-log(prob),也即是最大概率)的算法。
———————————————————————————————————————————
HMM(隐马尔可夫模型)是用来描述隐含未知参数的统计模型,举一个经典的例子:一个东京的朋友每天根据天气{下雨,天晴}决定当天的活动{公园散步,购物,清理房间}中的一种,我每天只能在twitter上看到她发的推“啊,我前天公园散步、昨天购物、今天清理房间了!”,那么我可以根据她发的推特推断东京这三天的天气。在这个例子里,显状态是活动,隐状态是天气。
任何一个HMM都可以通过下列五元组来描述:
:param obs:观测序列
:param states:隐状态
:param start_p:初始概率(隐状态)
:param trans_p:转移概率(隐状态)
:param emit_p: 发射概率 (隐状态表现为显状态的概率)四、隐马尔可夫模型在交通方向的应用
隐马尔可夫模型(Hidden Markov Model,HMM)最早用于语音的模式识别,国外研究学者对于 HMM 在交通方向也有了一些比较成熟的应用。
Jun Z 等人以交通事故多发地点道路交叉口为研究对象,交叉口的车辆运行情况比较复杂,其交通冲突的检测识别便会非常困难,实测道路交叉口产生交通冲突的车辆运动数据,运用 HMM 对车与车间的交通冲突进行识别分类,验证分类效果较好,可以实现交叉口危险状态及碰撞等交通事故的预测。
Saunier N 和Sayed T 的研究目的为使用视频传感器进行道路安全自主分析以缓解车辆碰撞带来的负面影响,提出了聚类车辆轨迹隐马尔可夫模型,通过检测到的交通冲突识别和调整冲突轨迹模型。
Li K 等人提出了一种新的算法,结合 HMM和贝叶斯滤波(BF)技术,以识别一个驾驶员的变道意图。HMM 的输出是是对驾驶行为的初步分类,至于 BF 是对 HMM 输出行为的最终分类过程。
Al Machot F 将隐马尔可夫模型应用于交叉口交通网络 OD 交通流的预测,OD 矩阵对于各项规划以及操作任务是非常有用的,并且用两个不同的十字路口的情境数据进行了模型的评价。
Meng X 等人基于动态驾驶行为提出了一个智能车辆防盗系统,使用隐马尔可夫模型对个人驾驶行为进行学习。
国内 HMM 在交通领域的应用比较成熟的为驾驶意图的识别。
宗长富等人构建了双层隐马尔可夫模型包含下层操作层 HMM 和上层意图层 HMM,其中下层 HMM 操作层包含制动与加速、转向、车速三方面,在意图层得到单一及复合工况下的驾驶员驾驶意图。
许晓明使用 SMI-HED 头盔式眼动仪采集驾驶员的眼部信息,用摄像机采集驾驶员面部信息,建立隐马尔可夫模型来反映驾驶员精神状态变化的时间序列过程,用来描述驾驶员在道路上疲劳驾驶评估模型。
曹凯等人为了解决交通场景理解中车辆的机动行为识别问题,提出了基于多隐马尔可夫模型(M-HMM)的多目标时空依赖关系模型,这有助于未来车辆自动驾驶实现。
吴志周等人以公交驾驶险态行为为研究对象,结合 10 位公交车驾驶员的运行数据,从公交驾驶、启动、驻车稳定性以及疲劳驾驶四种险态行为提取七个特征因子,建立了隐马尔可夫统计模型。
赵志国综述了隐 Markov 模型本身特有的模式识别特点在智能交通领中的应用及前景展望,其中 HMM在驾驶员驾驶意图、汽车碰撞预测以及交通流相关智能检测等方面得到了良好的应用。
吕岸等人采用高斯混合 HMM 对高速公路的正常超车行为以及不正常超车行为进行识别。
杨江波建立了交通流 HMM来对短时交通流状态进行预测,短时间内交通流状态预测能够为道路使用者提供预测信息,从而提前制定出行计划。
喻丹研究驾驶人超车行为时,将超车行为拆解为车辆换道和车辆切入两部分的组合行为,建立了改进二维 HMM来识别超车行为,该模型不仅能够识别正常超车及非正常右侧超车行为,还能够实现超车行为的提前预警。
———————————————————————————————————————————
隐马尔可夫模型(Hidden Markov Model,HMM)是用单个离散随机变量描述过程状态的时序概率模型,它是结构最简单的动态贝叶斯网络(Dynamic Bayesian Network,DBN)。在绪论中已经介绍过,在进行驾驶员行为分析时动态贝叶斯网络被广泛应用,典型的贝叶斯网络结构如图 1.8 所示。每个离散变量的动态贝叶斯网络都可以表示成一个隐马尔可夫模型,如果有多个状态变量,则可以将所有状态变量合并成一个单一的状态变量,其取值为各单个状态变量取值组成的所有可能元组。隐马尔可夫模型这种简单明快的结构使得它在时序数据建模方面有着广泛的应用,例如语音识别、自然语言处理[88]等领域。
在实际应用中,关于隐马尔可夫模型常关注三个基本问题:
1. 已知模型,若有观测序列 = 12… ,如何衡量观测序列与模型之间的匹配程度,即计算概率(|)?
2. 已知模型λ和观测序列 = 12… ,如何推测系统可能的隐藏状态序列 =12… ?
3. 已知观测序列 = … 和模型结构,如果估计出使得该序列出现概率最大的模型参数?
主要参考:
[1]罗沂. 基于GPS数据的高速公路驾驶行为识别[D]. 哈尔滨工业大学.
[2]吉文超. 基于驾驶行为分析的城市道路车辆换道模型研究[D]. 哈尔滨工业大学.
[3]卢锡凤. 基于隐马尔可夫模型的城市道路路段不良驾驶行为鉴别[D]. 哈尔滨工业大学.
[4]李建平. 面向智能驾驶的交通车辆运动预测方法研究[D]. 吉林大学.