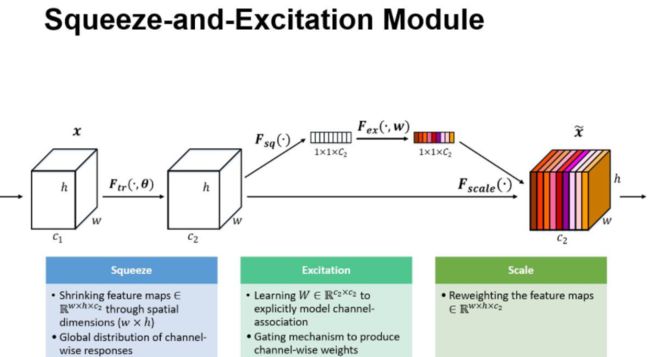
SE （Squeeze Excitation）模块

常规卷积操作会对输入各个通道做卷积，然后对个通道的卷积结果进行求和，这种操作将卷积学习到的空间特征和通道特征混合在一起；而 SE 模块就是为了抽离这种混杂，让模型直接学习通道特征。

SE 模块显式地建模特征通道之间的相互依赖关系，通过学习的方式获取每个 channel 的重要程度，然后依照这个重要程度来对各个通道上的特征进行加权，从而突出重要特征，抑制不重要的特征。简单说就是训练一组权重，对各个 channel 的特征图加权。
本质上，SE 模块是在 channel 维度上做 attention 或者 gating 操作，这种注意力机制让模型可以更加关注重要的 channel 的特征。SE模块可以轻松的移植到其他网络架构，能够以轻微的计算性能损失带来极大的准确率提升。

Ftr 是常规的卷积操作；U 后面是SE模块，包含 squeeze 和 excitation 两步；

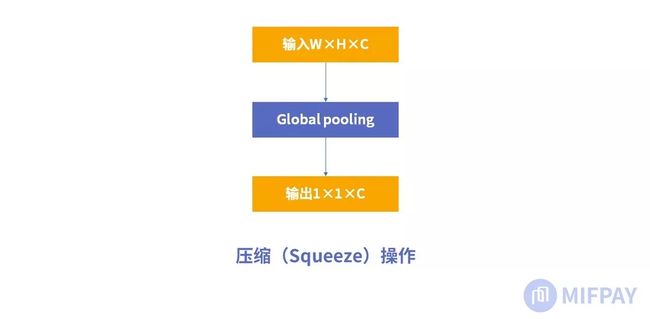
1. 压缩（squeeze ）

由于卷积只是在局部空间内进行操作（没有全局感受野），很难获得做够的信息来提取 channel 之间的关系特征。 为了提取 channel 之间的关系，首先要将每个 channel 上的空间特征编码（压缩）为一个全局特征（可以理解为对每个 channel 的特征信息的进行融合），采用全局平局池化来实现，输出维度为1x1xC。

 2. 激励（Excitation）

得到Squeeze的1x1xC全局特征后，加入一个FC全连接层（Fully Connected），对每个通道的重要性进行预测，得到不同channel的重要性大小后再作用（激励）到之前的feature map的对应channel上，再进行后续操作。

由两个全连接层组成，其中SERatio是一个缩放参数，这个参数的目的是为了减少通道个数从而降低计算量。 第一个全连接层有C*SERatio个神经元，输入为1×1×C，输出1×1×C×SERadio，起到降维作用。 第二个全连接层有C个神经元，输入为1×1×C×SERadio，输出为1×1×C。

3. Scale

最后是scale操作，在得到1×1×C向量之后，就可以对原来的特征图进行scale操作了。很简单，就是通道权重相乘，原有特征向量为W×H×C，将SE模块计算出来的各通道权重值分别和原特征图对应通道的二维矩阵相乘，得出的结果输出。

这里我们可以得出SE模块的属性：

参数量 = 2×C×C×SERatio

计算量 = 2×C×C×SERatio 

总体来讲SE模块会增加网络的总参数量，总计算量，因为使用的是全连接层计算量相比卷积层并不大，但是参数量会有明显上升，所以MobileNetV3-Large中的总参数量比MobileNetV2多了2M。

SE实现注意力机制原因：

SE可以实现注意力机制最重要的两个地方一个是全连接层，另一个是相乘特征融合；

假设输入图像H×W×C，通过global pooling+FC层，拉伸成1×1×C，然后再与原图像相乘，将每个通道赋予权重。在去噪任务中，将每个噪声点赋予权重，自动去除低权重的噪声点，保留高权重噪声点，提高网络运行时间，减少参数计算。这也就是SE模块具有attention机制的原因。

5. MobileNet中的SE模块

SE模块的使用是很灵活的，可以在已有网络上添加而不打乱网络原有的主体结构。
ResNet中添加SE模块形成SE-ResNet网络，SE模块是在bottleneck结构之后加入的，如下图左边所示。

MobileNetV3版本中SE模块加在了bottleneck结构的内部，在深度卷积后增加SE块，scale操作后再做逐点卷积，如上图右边所示。MobileNetV3版本的SERadio系数为0.25。使用SE模块后的MobileNetV3的参数量相比MobileNetV2多了约2M，达到5.4M，但是MobileNetV3的精度得到了很大的提升，在图像分类和目标检测中准确率都有明显提升。

import torch
import torch.nn as nn

# 定义residual
class RB(nn.Module):
    def __init__(self, nin, nout, ksize=3, stride=1, pad=1):
        super(RB, self).__init__()
        self.rb = nn.Sequential(nn.Conv2d(nin, nout, ksize, stride, pad),
                                nn.BatchNorm2d(nout),
                                nn.ReLU(inplace=True),
                                nn.Conv2d(nout, nout, ksize, stride, pad),
                                nn.BatchNorm2d(nout))
    def forward(self, input):
        x = input
        x = self.rb(x)
        return nn.ReLU(input + x)

# 定义SE模块
class SE(nn.Module):
    def __init__(self, nin, nout, reduce=16):
        super(SE, self).__init__()
        self.gp = nn.AvgPool2d(1)
        self.rb1 = RB(nin, nout)
        self.se = nn.Sequential(nn.Linear(nout, nout // reduce),
                                nn.ReLU(inplace=True),
                                nn.Linear(nout // reduce, nout),
                                nn.Sigmoid())
    def forward(self, input):
        x = input
        x = self.rb1(x)

        b, c, _, _ = x.size()
        y = self.gp(x).view(b, c)
        y = self.se(y).view(b, c, 1, 1)
        y = x * y.expand_as(x)
        out = y + input
        return out
net=SE(64,64)
print(net)