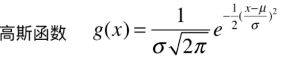SVM深入理解：解决线性不可分类时，对特征集进行多项式、核函数转换将其转换为线性可分类问题

一、核函数

1.格式

• K(x, y)：表示样本 x 和 y，添加多项式特征得到新的样本 x’、y’，K(x, y) 就是返回新的样本经过计算得到的值；
• 在 SVM 类型的算法 SVC() 中，K(x, y) 返回点乘：x’ . y’ 得到的值；
  

2.多项式核函数

内部实现：

（1）对传入的样本数据点添加多项式项；
（2）新的样本数据点进行点乘，返回点乘结果；
多项式特征的基本原理：依靠升维使得原本线性不可分的数据线性可分；
升维的意义：使得原本线性不可分的数据线性可分；
例：
一维特征的样本，两种类型，分布如图，线性不可分：

为样本添加一个特征：x2 ，使得样本在二维平面内分布，此时样本在 x 轴升的分布位置不变；如图，可以线性可分：

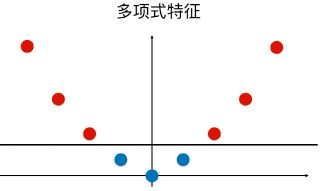
3.优点 / 特点

• 不需要每次都具体计算出原始样本点映射的新的无穷维度的样本点，直接使用映射后的新的样本点的点乘计算公式即可；
• 减少计算量
• 减少存储空间
• 一般将原始样本变形，通常是将低维的样本数据变为高维数据，存储高维数据花费较多的存储空间；使用核函数，不用考虑原来样本改变后的样子，也不用存储变化后的结果，只需要直接使用变化的结果进行运算并返回运算结果即可；
• 核函数的方法和思路不是 SVM 算法特有，只要可以减少计算量和存储空间，都可以设计核函数方便运算；
• 对于比较传统的常用的机器学习算法，核函数这种技巧更多的在 SVM 算法中使用；

4.SVM 中的核函数

• svm 类中的 SVC() 算法中包含两种核函数：
• SVC(kernel = ‘ploy’)：表示算法使用多项式核函数；
• SVC(kernel = ‘rbf’)：表示算法使用高斯核函数；
• SVM 算法的本质就是求解目标函数的最优化问题；
  
  求解最优化问题时，将数学模型变形：
  

5.多项式核函数

格式：
from sklearn.svm import SVC
svc = SVC(kernel = ‘ploy’)

**思路：**设计一个函数（ K(xi, xj) ），传入原始样本（x(i) 、 x(j)），返回添加了多项式特征后的新样本的计算结果（x’(i) . x’(j)）；
内部过程：先对 xi 、xj 添加多项式，得到：x’(i) 、 x’(j) ，再进行运算：x’(i) . x’(j) ；
x(i) 添加多项式特征后：x’(i) ；
x(j) 添加多项式特征后：x’(j) ；
x(i) . x(j) 转化为：x’(i) . x’(j) ；
其实不使用核函数也能达到同样的目的，这里核函数相当于一个技巧，更方便运算；

二、高斯核函数（RBF）

1.思想

• 业务的目的是样本分类，采用的方法：按一定规律统一改变样本的特征数据得到新的样本，新的样本按新的特征数据能更好的分类，由于新的样本的特征数据与原始样本的特征数据呈一定规律的对应关系，因此根据新的样本的分布及分类情况，得出原始样本的分类情况。
• 应该是试验反馈，将样本的特征数据按一定规律统一改变后，同类样本更好的凝聚在了一起；
• 高斯核和多项式核干的事情截然不同的，如果对于样本数量少，特征多的数据集，高斯核相当于对样本降维；

高斯核的任务：找到更有利分类任务的新的空间。
方法：类似 的映射。
高斯核本质是在衡量样本和样本之间的“相似度”，在一个刻画“相似度”的空间中，让同类样本更好的聚在一起，进而线性可分。

2.定义方式

（1）x、y：样本或向量；
（2）γ：超参数；高斯核函数唯一的超参数；
（3）|| x - y ||：表示向量的范数，可以理解为向量的模；
（4）表示两个向量之间的关系，结果为一个具体值；
（5）高斯核函数的定义公式就是进行点乘的计算公式；

3.功能

• 先将原始的数据点（x， y）映射为新的样本（x’，y’）；
• 再将新的特征向量点乘（x’ . y’），返回其点乘结果；
• 计算点积的原因：此处只针对 SVM 中的应用，在其它算法中的应用不一定需要计算点积；
  

4.特点

• 高斯核运行开销耗时较大，训练时间较长；
• 一般使用场景：数据集 (m, n)，m < n；
• 一般应用领域：自然语言处理；
  自然语言处理：通常会构建非常高维的特征空间，但有时候样本数量并不多；

5.高斯函数

• 正态分布就是一个高斯函数；
• 高斯函数和高斯核函数，形式类似；

6.其它

• 高斯核函数，也称为 RBF 核（Radial Basis Function Kernel），也称为径向基函数；
• 高斯核函数的本质：将每一个样本点映射到一个无穷维的特征空间；
• 无穷维：将 mn 的数据集，映射为 mm 的数据集，m 表示样本个数，n 表示原始样本特征种类，样本个数是无穷的，因此，得到的新的数据集的样本也是无穷维的；
• 高斯核升维的本质，使得线性不可分的数据线性可分；

三、重做例子代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC 
iris = datasets.load_iris()
X=iris.data
y=iris.target
X=X[y<2,:2]#只取y<2的类别，也就是0 1 并且只取前两个特征 
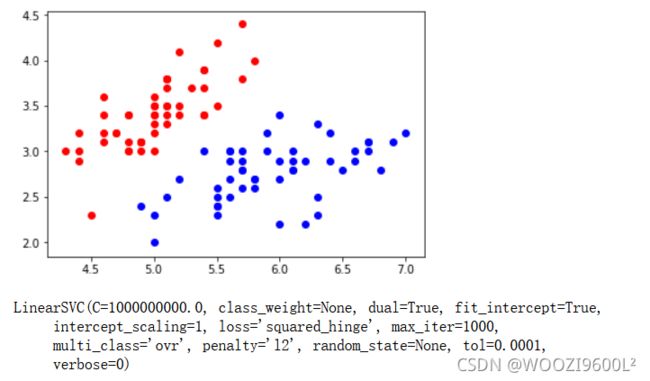
y=y[y<2]# 只取y<2的类别 # 分别画出类别0和1的点 
plt.scatter(X[y==0,0],X[y==0,1],color='red')
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()
# 标准化 
standardScaler=StandardScaler()
standardScaler.fit(X)#计算训练数据的均值和方差 
X_standard=standardScaler.transform(X)#再用scaler中的均值和方差来转换X，使X标准化 
svc=LinearSVC(C=1e9)#线性SVM分类器 
svc.fit(X_standard,y)# 训练svm

def plot_decision_boundary(model, axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    X_new=np.c_[x0.ravel(),x1.ravel()]
    y_predict=model.predict(X_new)
    zz=y_predict.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_cmap)# 绘制决策边界 
warnings.filterwarnings("ignore")
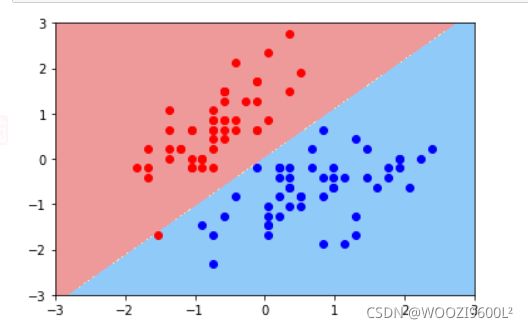
plot_decision_boundary(svc,axis=[-3,3,-3,3])# x,y轴都在-3到3之间 
# 绘制原始数据
plt.scatter(X_standard[y==0,0],X_standard[y==0,1],color='red')
plt.scatter(X_standard[y==1,0],X_standard[y==1,1],color='blue')
plt.show()

svc2=LinearSVC(C=0.01)
svc2.fit(X_standard,y)
plot_decision_boundary(svc2,axis=[-3,3,-3,3])# x,y轴都在-3到3之间 
# 绘制原始数据 
plt.scatter(X_standard[y==0,0],X_standard[y==0,1],color='red')
plt.scatter(X_standard[y==1,0],X_standard[y==1,1],color='blue')
plt.show()

# 接下来我们看下如何处理非线性的数据。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
X, y = datasets.make_moons() #使用生成的数据 
print(X.shape) # (100,2) 
print(y.shape) # (100,)
# 接下来绘制下生成的数据
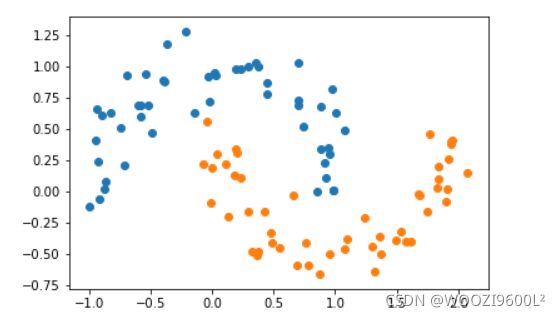
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

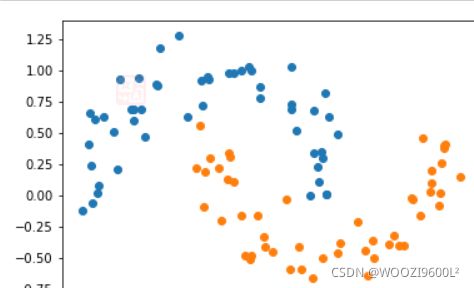
X,  y = datasets.make_moons(noise=0.15,random_state=777) 
#随机生成噪声点，random_state是随机种子，noise是方差
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
def PolynomialSVC(degree,C=1.0):
    return Pipeline([ ("poly",PolynomialFeatures(degree=degree)),#生成多项式 
                     ("std_scaler",StandardScaler()),#标准化 
                     ("linearSVC",LinearSVC(C=C))#最后生成svm 
                    ])
poly_svc = PolynomialSVC(degree=3)
poly_svc.fit(X,y)
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

from sklearn.svm import SVC
def PolynomialKernelSVC(degree,C=1.0):
    return Pipeline([ ("std_scaler",StandardScaler()), 
                     ("kernelSVC",SVC(kernel="poly"))# poly代表多项式特征 
                    ])
poly_kernel_svc = PolynomialKernelSVC(degree=3) 
poly_kernel_svc.fit(X,y)
plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

import numpy as np 
import matplotlib.pyplot as plt
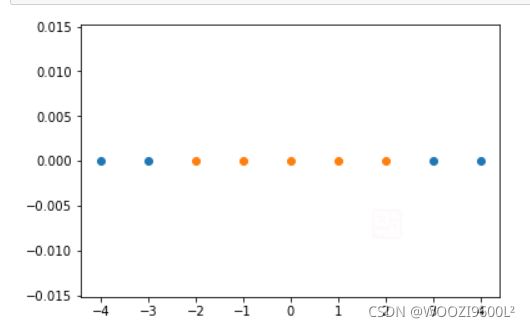
x = np.arange(-4,5,1)
#生成测试数据
y = np.array((x >= -2 ) & (x <= 2),dtype='int')
plt.scatter(x[y==0],[0]*len(x[y==0]))
# x取y=0的点, y取0，有多少个x，就有多少个y
plt.scatter(x[y==1],[0]*len(x[y==1]))
plt.show()

# 高斯核函数 
def gaussian(x,l):
    gamma = 1.0
    return np.exp(-gamma * (x -l)**2)
l1,l2 = -1,1
X_new = np.empty((len(x),2))#len(x) ,2 
for i,data in enumerate(x):
    X_new[i,0] = gaussian(data,l1)
    X_new[i,1] = gaussian(data,l2)
    plt.scatter(X_new[y==0,0],X_new[y==0,1])
    plt.scatter(X_new[y==1,0],X_new[y==1,1])
    plt.show()

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
X,y = datasets.make_moons(noise=0.15,random_state=777)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
def RBFKernelSVC(gamma=1.0):
    return Pipeline([ ('std_scaler',StandardScaler()), ('svc',SVC(kernel='rbf',gamma=gamma)) ])
svc = RBFKernelSVC()
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
def RBFKernelSVC(gamma=100):
    return Pipeline([ ('std_scaler',StandardScaler()), ('svc',SVC(kernel='rbf',gamma=gamma)) ])
svc = RBFKernelSVC()
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
def RBFKernelSVC(gamma=10):
    return Pipeline([ ('std_scaler',StandardScaler()), ('svc',SVC(kernel='rbf',gamma=gamma)) ])
svc = RBFKernelSVC()
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
def RBFKernelSVC(gamma=0.1):
    return Pipeline([ ('std_scaler',StandardScaler()), ('svc',SVC(kernel='rbf',gamma=gamma)) ])
svc = RBFKernelSVC()
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()
X = boston.data
y = boston.target
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=777)
# 把数据集拆分成训练数据和测试数据
from sklearn.svm import LinearSVR
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
def StandardLinearSVR(epsilon=0.1):
    return Pipeline([ ('std_scaler',StandardScaler()), ('linearSVR',LinearSVR(epsilon=epsilon)) ])
svr = StandardLinearSVR()
svr.fit(X_train,y_train)
svr.score(X_test,y_test)

四、对鸢尾花、月亮数据集进行SVM训练

1、鸢尾花数据集

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets, svm
import pandas as pd
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
iris = datasets.load_iris()
iris = datasets.load_iris()
X = iris.data                  
y = iris.target                
X = X[y != 0, :2]             # 选择X的前两个特性
y = y[y != 0]
n_sample = len(X)              
np.random.seed(0)
order = np.random.permutation(n_sample)  # 排列，置换
X = X[order]
y = y[order].astype(np.float)
X_train = X[:int(.9 * n_sample)]
y_train = y[:int(.9 * n_sample)]
X_test = X[int(.9 * n_sample):]
y_test = y[int(.9 * n_sample):]
#合适的模型
for fig_num, kernel in enumerate(('linear', 'rbf','poly')):  # 径向基函数 (Radial Basis Function 简称 RBF),常用的是高斯基函数
    clf = svm.SVC(kernel=kernel, gamma=10)   # gamma是“rbf”、“poly”和“sigmoid”的核系数。
    clf.fit(X_train, y_train)
    plt.figure(str(kernel))
    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.scatter(X[:, 0], X[:, 1], c=y, zorder=10, cmap=plt.cm.Paired, edgecolor='k', s=20)
    # zorder: z方向上排列顺序，数值越大，在上方显示
    # paired两个色彩相近输出(paired)
    # 圈出测试数据
    plt.scatter(X_test[:, 0], X_test[:, 1], s=80, facecolors='none',zorder=10, edgecolor='k')
    plt.axis('tight')  #更改 x 和 y 轴限制，以便显示所有数据
    x_min = X[:, 0].min()
    x_max = X[:, 0].max()
    y_min = X[:, 1].min()
    y_max = X[:, 1].max()
    XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]   
    Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()])  # 样本X到分离超平面的距离
    Z = Z.reshape(XX.shape)
    plt.contourf(XX,YY,Z>0,cmap=plt.cm.Paired)  
    plt.contour(XX, YY, Z, colors=['r', 'k', 'b'],
                linestyles=['--', '-', '--'], levels=[-0.5, 0, 0.5])   # 范围
    plt.title(kernel)
plt.show()

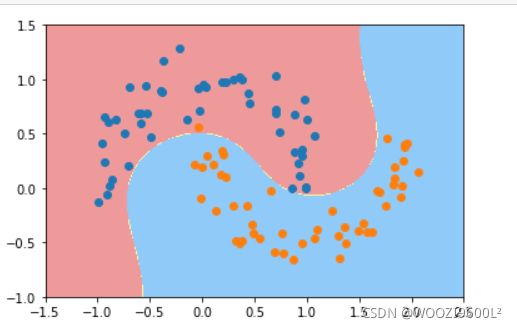
2.月亮数据集

多项式核

# 导入月亮数据集和svm方法
#这是多项式核svm
mpl.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
mpl.rcParams['axes.unicode_minus']=False #用来正常显示负号
from sklearn import datasets #导入数据集
from sklearn.svm import LinearSVC #导入线性svm
from sklearn.pipeline import Pipeline #导入python里的管道
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler,PolynomialFeatures #导入多项式回归和标准化
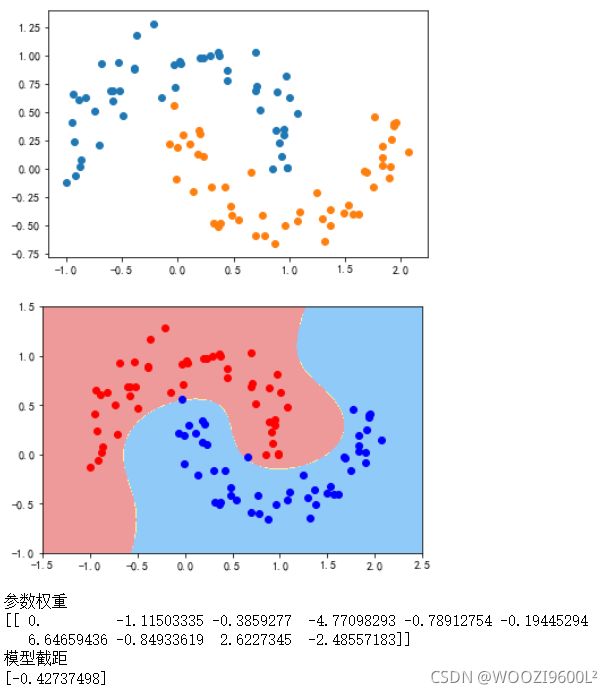
data_x,data_y=datasets.make_moons(noise=0.15,random_state=777)#生成月亮数据集
# random_state是随机种子，nosie是方
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1])
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1])
data_x=data_x[data_y<2,:2]#只取data_y小于2的类别，并且只取前两个特征
plt.show()
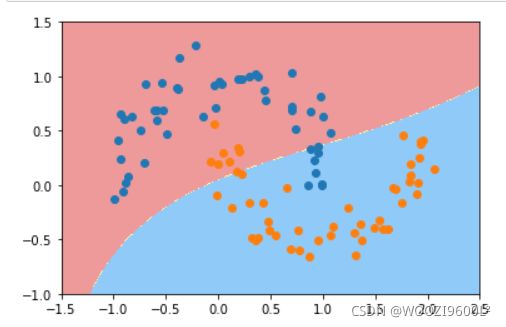
def PolynomialSVC(degree,c=10):#多项式svm
    return Pipeline([
            # 将源数据 映射到 3阶多项式
            ("poly_features", PolynomialFeatures(degree=degree)),
            # 标准化
            ("scaler", StandardScaler()),
            # SVC线性分类器
            ("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42,max_iter=10000))
        ])
# 进行模型训练并画图
poly_svc=PolynomialSVC(degree=3)
poly_svc.fit(data_x,data_y)
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])#绘制边界
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')#画点
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()
print('参数权重')
print(poly_svc.named_steps['svm_clf'].coef_)
print('模型截距')
print(poly_svc.named_steps['svm_clf'].intercept_)

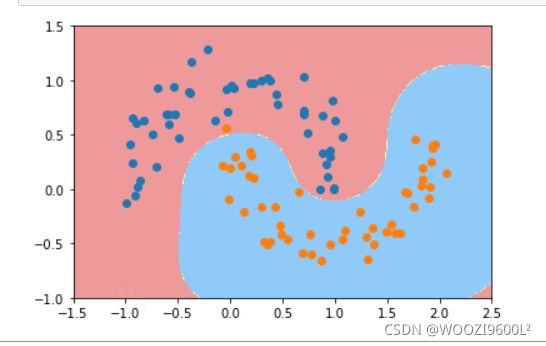
高斯核

## 导入包
from sklearn import datasets #导入数据集
from sklearn.svm import SVC #导入svm
from sklearn.pipeline import Pipeline #导入python里的管道
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler#导入标准化
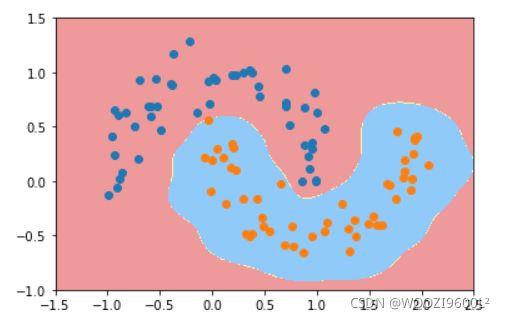
def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])
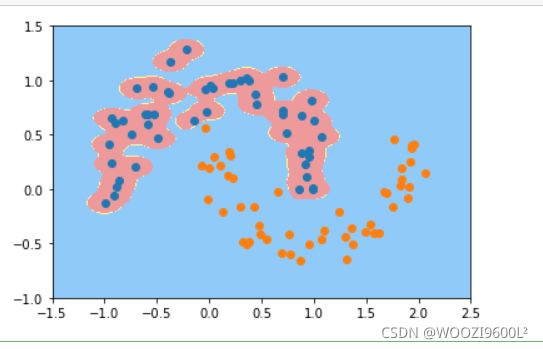
svc=RBFKernelSVC(gamma=100)#gamma参数很重要，gamma参数越大，支持向量越小
svc.fit(data_x,data_y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')#画点
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()

五、总结

SVM通过多项式核函数、高斯核函数等实现对数据的分类处理，更加精准。

参考资料

https://www.cnblogs.com/volcao/p/9465214.html
http://blog.sina.com.cn/s/blog_6c3438600102yn9x.html
https://blog.csdn.net/weixin_43869980/article/details/106336343?spm=1001.2014.3001.5501