深度学习框架TensorFlow2初步入门学习

TensorFlow2入门学习

TensorFlow 2 新增变化特性

TensorFlow 2 安装

2019 年初，TensorFlow 官方推出了 2.0 预览版本，也意味着 TensorFlow 即将从 1.x 过度到 2.x 时代。

根据 TensorFlow 官方介绍内容 显示，2.0 版本将专注于简洁性和易用性的改善，主要升级方向包括：

• 使用 Keras 和 Eager Execution 轻松构建模型。
• 在任意平台上实现稳健的生产环境模型部署。
• 为研究提供强大的实验工具。
• 通过清理废弃的 API 和减少重复来简化 API。

接下来，加载 TensorFlow 并查看版本号，看是否已经为 2.x。

In [ ]:

import tensorflow as tf

tf.__version__

Eager Execution

TensorFlow 2 带来的最大改变之一是将 1.x 的 Graph Execution（图与会话机制）更改为 Eager Execution（动态图机制）。在 1.x 版本中，低级别 TensorFlow API 首先需要定义数据流图，然后再创建 TensorFlow 会话，这一点在 2.0 中被完全舍弃。

TensorFlow 2 中的 Eager Execution 是一种命令式编程环境，可立即评估操作，无需构建图：操作会返回具体的值，而不是构建以后再运行的计算图。实际上，Eager Execution 在 1.x 的后期版本中也存在，但需要单独执行 tf.enable_eager_execution() 进行手动启用。不过，2.0 版本的 TensorFlow 默认采用了 Eager Execution，无法关闭并回到 1.x 的 Graph Execution 模式中。

下面，我们来演示 Eager Execution 带来的变化。

1.x 版本中，如果我们新建一个张量 tf.Variable([[1, 2], [3, 4]]) 并执行输出，那么只能看到这个张量的形状和属性，并不能直接输出其数值。结果如下：

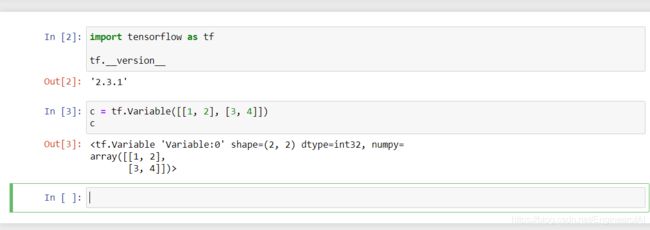
如今，Eager Execution 模式下则可以直接输出张量的数值了，并以 NumPy 数组方式呈现。

c = tf.Variable([[1, 2], [3, 4]])
c

你还可以直接通过 .numpy() 输出张量的 NumPy 数组。Eager Execution 适合与 NumPy 一起使用。NumPy 操作接受 tf.Tensor 参数。TensorFlow 数学运算将 Python 对象和 NumPy 数组转换为 tf.Tensor 对象。tf.Tensor.numpy 方法返回对象的值作为 NumPy ndarray。

c.numpy()

Eager Execution 带来的好处是不再需要手动管理图和会话。例如，现在使用示例张量进行数学计算，可以像 Python 一样直接相加。

c + c  # 加法计算

而在 1.x 版本中，我们需要初始化全局变量 → 建立会话 → 执行计算，最终才能打印出张量的运算结果。

init_op = tf.global_variables_initializer()  # 初始化全局变量
with tf.Session() as sess:  # 启动会话
    sess.run(init_op)
    print(sess.run(c + c))  # 执行计算

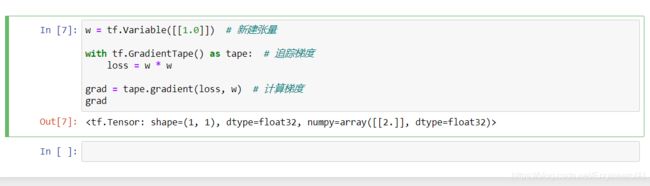
Eager Execution 带来的好处显而易见，其进一步降低了 TensorFlow 的入门门槛。之前，因为图与会话的模式，让很多人在入门时都很纳闷。除此之外，得益于自动微分的使用，在 Eager Execution 期间，可以使用 tf.GradientTape 这类跟踪操作以便稍后计算梯度。

In [1]:

w = tf.Variable([[1.0]])  # 新建张量

with tf.GradientTape() as tape:  # 追踪梯度
    loss = w * w

grad = tape.gradient(loss, w)  # 计算梯度
grad
---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
<ipython-input-1-1e9ac7891209> in <module>
----> 1 w = tf.Variable([[1.0]])  # 新建张量
      2 
      3 with tf.GradientTape() as tape:  # 追踪梯度
      4     loss = w * w
      5 

NameError: name 'tf' is not defined

`tf.GradientTape` 会像磁带一样记录下计算图中的梯度信息，然后使用 `.gradient` 即可回溯计算出任意梯度，这对于使用 TensorFlow 低阶 API 构建神经网络时更新参数非常重要。

Markdown Code

`tf.GradientTape` 会像磁带一样记录下计算图中的梯度信息，然后使用 `.gradient` 即可回溯计算出任意梯度，这对于使用 TensorFlow 低阶 API 构建神经网络时更新参数非常重要。

Eager Execution 的好处很多，但带来的问题也是很明显的，尤其是对于已经熟练使用 TensorFlow 的工程师而言简直是噩梦。

如今，TensorFlow 的默认执行模式为 Eager Execution，这就意味着之前基于 Graph Execution 构建的代码将完全无法使用，因为 2.0 中已经没有了相应的 API。例如，先前构建神经网络计算图时，都习惯于使用 tf.placeholder 占位符张量，等最终执行时再传入数据。Eager Execution 模式下，tf.placeholder 已无存在必要，所以此 API 已被移除。

所以，随着 TensorFlow 2 默认引入 Eager Execution 机制，也就意味着原 1.x 低阶 API 构建图的方法后续已无法使用。

TensorFlow Keras

TensorFlow 1.x 中，我们可以通过 tf.layers 高阶层封装开快速搭建神经网络。如果，2.0 已完全移除了 tf.layers 模块，转而引入了 tf.keras。

如果你熟悉 Keras 的使用，那么 tf.keras 用起来就得心应手了，因为其基本和单独发行版本一致，子模块结构也几乎完全一样。除此之外，原 tf.contrib 也已经在 2.0 版本中被移除。

TensorFlow2实现线性回归

低阶 API 实现

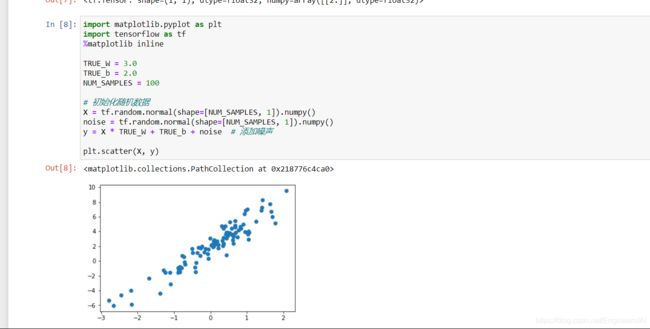
低阶 API 实现，实际上就是利用 Eager Execution 机制来完成。实验首先初始化一组随机数据样本，并添加噪声，然后将其可视化出来。

低阶 API 实现，实际上就是利用 Eager Execution 机制来完成。实验首先初始化一组随机数据样本，并添加噪声，然后将其可视化出来。

import matplotlib.pyplot as plt
import tensorflow as tf
%matplotlib inline

TRUE_W = 3.0
TRUE_b = 2.0
NUM_SAMPLES = 100

# 初始化随机数据
X = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()
noise = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()
y = X * TRUE_W + TRUE_b + noise  # 添加噪声

plt.scatter(X, y)

接下来，我们定义一元线性回归模型。

f,,)=∗+f(w,b,x)=w∗x+b

这里我们构建自定义模型类，并使用 TensorFlow 提供的 tf.Variable 随机初始化参数 w 和截距项 b。

class Model(object):
    def __init__(self):
        self.W = tf.Variable(tf.random.uniform([1]))  # 随机初始化参数
        self.b = tf.Variable(tf.random.uniform([1]))

    def __call__(self, x):
        return self.W * x + self.b  # w*x + b

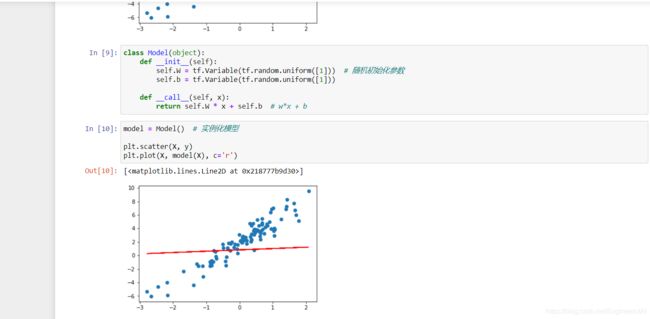
对于随机初始化的 w 和 b，我们可以将其拟合直线绘制到样本散点图中。

model = Model()  # 实例化模型

plt.scatter(X, y)
plt.plot(X, model(X), c='r')

可以明显看出，直线并没有很好地拟合样本。当然，由于是随机初始化，也有极小概率一开始拟合效果非常好，那么重新执行一次上面的单元格另外随机初始化一组数据即可。

然后，我们定义线性回归使用到的损失函数。这里使用线性回归问题中常用的平方损失函数。对于线性回归问题中与数学相关的知识点，本次实验不再推动和讲解。

Loss(,,,)=∑=1((,,)−)2Loss(w,b,x,y)=∑i=1N(f(w,b,xi)−yi)2

根据公式实现损失计算函数。

In [ ]:

def loss_fn(model, x, y):
    y_ = model(x)
    return tf.reduce_mean(tf.square(y_ - y))

接下来，就可以开始迭代过程了，这也是最关键的一步。使用迭代方法求解线性回归的问题中，我们首先需要计算参数的梯度，然后使用梯度下降法来更新参数。

←−∗∂loss(,)∂←−∗∂loss(,)∂w←w−lr∗∂loss(w,b)∂w b←b−lr∗∂loss(w,b)∂b

公式中，lr 指代学习率。

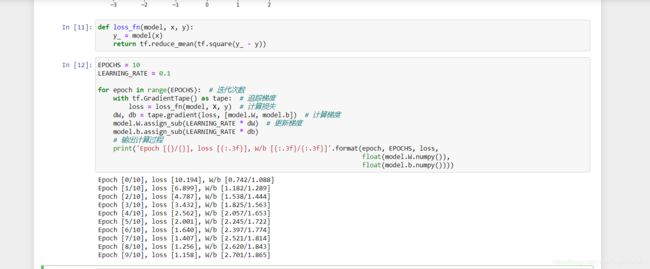
TensorFlow 2 中的 Eager Execution 提供了 tf.GradientTape 用于追踪梯度。所以，下面我们就实现梯度下降法的迭代更新过程。

In [ ]:

EPOCHS = 10
LEARNING_RATE = 0.1

for epoch in range(EPOCHS):  # 迭代次数
    with tf.GradientTape() as tape:  # 追踪梯度
        loss = loss_fn(model, X, y)  # 计算损失
    dW, db = tape.gradient(loss, [model.W, model.b])  # 计算梯度
    model.W.assign_sub(LEARNING_RATE * dW)  # 更新梯度
    model.b.assign_sub(LEARNING_RATE * db)
    # 输出计算过程
    print('Epoch [{}/{}], loss [{:.3f}], W/b [{:.3f}/{:.3f}]'.format(epoch, EPOCHS, loss,
                                                                     float(model.W.numpy()),
                                                                     float(model.b.numpy())))

上面的代码中，我们初始化 tf.GradientTape() 以追踪梯度，然后使用 tape.gradient 方法就可以计算梯度了。值得注意的是，tape.gradient() 第二个参数支持以列表形式传入多个参数同时计算梯度。紧接着，使用 .assign_sub 即可完成公式中的减法操作用以更新梯度。

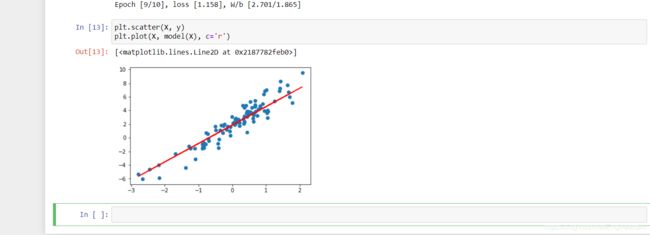
最终，我们绘制参数学习完成之后，模型的拟合结果。

In [ ]:

plt.scatter(X, y)
plt.plot(X, model(X), c='r')

如无意外，你将得到一个比随机参数好很多的拟合直线。

提示：由于是随机初始化参数，如果迭代后拟合效果仍然不好，一般是迭代次数太少的原因。你可以重复执行上面的迭代单元格多次，增加参数更新迭代次数，即可改善拟合效果。此提示对后面的内容同样有效。

高阶 API 实现

TensorFlow 2 中提供了大量的高阶 API 帮助我们快速构建所需模型，接下来，我们使用一些新的 API 来完成线性回归模型的构建。这里还是沿用上面提供的示例数据。

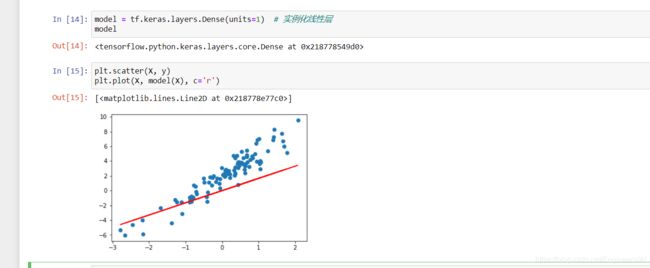
tf.keras 模块下提供的 tf.keras.layers.Dense 全连接层（线性层）实际上就是一个线性计算过程。所以，模型的定义部分我们就可以直接实例化一个全连接层即可。

In [ ]:

model = tf.keras.layers.Dense(units=1)  # 实例化线性层
model

其中，units 为输出空间维度。此时，参数已经被初始化了，所以我们可以绘制出拟合直线。

In [ ]:

plt.scatter(X, y)
plt.plot(X, model(X), c='r')

结果显示：

你可以使用 model.variables 打印出模型初始化的随机参数。

In [ ]:

model.variables

接下来就可以直接构建模型迭代过程了。

这里同样使用 tf.GradientTape() 来追踪梯度，我们简化损失计算和更新的过程。首先，损失可以使用现有 API tf.keras.losses.mean_squared_error 计算，最终使用 tf.reduce_sum 求得全部样本的平均损失。

In [ ]:

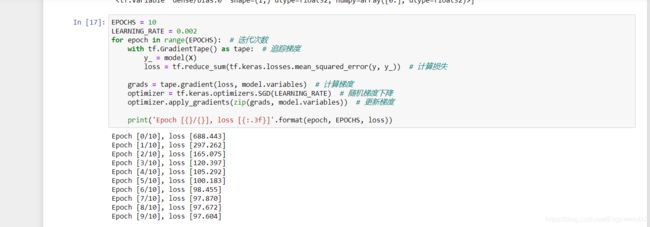
EPOCHS = 10
LEARNING_RATE = 0.002
for epoch in range(EPOCHS):  # 迭代次数
    with tf.GradientTape() as tape:  # 追踪梯度
        y_ = model(X)
        loss = tf.reduce_sum(tf.keras.losses.mean_squared_error(y, y_))  # 计算损失

    grads = tape.gradient(loss, model.variables)  # 计算梯度
    optimizer = tf.keras.optimizers.SGD(LEARNING_RATE)  # 随机梯度下降
    optimizer.apply_gradients(zip(grads, model.variables))  # 更新梯度

    print('Epoch [{}/{}], loss [{:.3f}]'.format(epoch, EPOCHS, loss))

其次，使用 model.variables 即可读取可参数的列表，无需像上面那样手动传入。这里不再按公式手动更新梯度，而是使用现有的随机梯度下降函数 tf.keras.optimizers.SGD，然后使用 apply_gradients 即可更新梯度。

最终，同样将迭代完成的参数绘制拟合直线到原图中。

In [ ]:

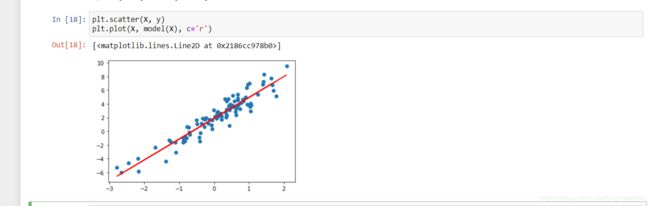
plt.scatter(X, y)
plt.plot(X, model(X), c='r')

如果拟合效果不好，请参考上文提示。

Keras 方式实现

上面的高阶 API 实现过程实际上还不够精简，我们可以完全使用 TensorFlow Keras API 来实现线性回归。

我们这里使用 Keras 提供的 Sequential 序贯模型结构。和上面的例子相似，向其中添加一个线性层。不同的地方在于，Keras 序贯模型第一层为线性层时，规定需指定输入维度，这里为 input_dim=1。

In [ ]:

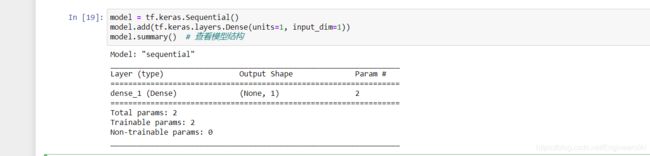
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(units=1, input_dim=1))
model.summary()  # 查看模型结构

接下来，直接使用 .compile 编译模型，指定损失函数为 MSE 平方损失，优化器选择 SGD 随机梯度下降。然后，就可以使用 .fit 传入数据开始迭代了。

In [ ]:

model.compile(optimizer='sgd', loss='mse')
model.fit(X, y, steps_per_epoch=100)

steps_per_epoch 只的是在默认小批量为 32 的条件下，传入相应次数的小批量样本。最终绘制出迭代完成的拟合图像。

In [ ]:

plt.scatter(X, y)
plt.plot(X, model(X), c='r')

如果拟合效果不好，请参考上文提示。

如上所示，完全使用 Keras 高阶 API 实际上只需要 4 行核心代码即可完成。相比于最开始的低阶 API 简化了很多。

TensorFlow 1.x 实现

为了与 TensorFlow 2 线性回归实现过程进行对比。最终，我们给出 TensorFlow 1.x 线性回归实现代码。这里，我们需要实验 TensorFlow 2 中 tensorflow.compat.v1 模块下提供的兼容性代码。

In [ ]:

import tensorflow.compat.v1 as tf

tf.disable_v2_behavior() # 关闭 Eager Execution 特性

接下来，就可以使用 TensorFlow 1.x 中提供的图与会话方式来实现线性回归过程了。

In [ ]:

X_train = tf.placeholder(tf.float32)  # 定义占位符张量
y_train = tf.placeholder(tf.float32)
W = tf.Variable(tf.random.normal([1]))  # 初始化参数
b = tf.Variable(tf.random.normal([1]))

LEARNING_RATE = 0.001  # 学习率

y_train_ = W*X_train + b  # 线性函数
loss = tf.reduce_mean(tf.square(y_train_ - y_train))  # 平方损失函数
optimizer = tf.train.GradientDescentOptimizer(
    LEARNING_RATE).minimize(loss)  # 梯度下降优化损失函数

EPOCHS = 1000  # 迭代次数
with tf.Session() as sess: # 启动会话
    tf.global_variables_initializer().run()  # 初始化全局变量
    for epoch in range(EPOCHS):  # 迭代优化
        sess.run(optimizer, feed_dict={X_train:X, y_train:y})
    final_weight = sess.run(W)  # 最终参数
    final_bias = sess.run(b)

print(final_weight, final_bias)

最后，我们依据迭代更新的参数，将拟合直线绘制到原图中。

In [ ]:

preds = final_weight * X + final_bias  # 计算预测值
plt.scatter(X, y)
plt.plot(X, preds, c='r')

实验总结

本次实验中，我们利用 TensorFlow 2 提供的 Eager Execution 实现了线性回归的经典过程。同时，利用 TensorFlow Keras 高阶 API 简化了实现步骤。实验的最后，使用 TensorFlow 1.x API 进行了对比示例，希望你能够准确把握 TensorFlow 2 和 1.0 之间的区别。

TensorFlow2构建前馈神经网络

低阶 API 构建

学习完线性回归中的低阶 API 实现方法，那么使用 TensorFlow 2 低阶 API 构建神经网络实际上就比较简单了。这里，我们先加载一组数据，DIGITS 数据集是 scikit-learn 提供的简单手写字符识别数据集。

我们读取数据集并进行简单切分，这里对字符标签进行了独热编码方便后面计算损失值。

In [1]:

import numpy as np
import tensorflow as tf
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split

digits = load_digits()
digits_y = np.eye(10)[digits.target.reshape(-1)]  # 标签独热编码
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits_y,
                                                    test_size=0.2, random_state=1)

X_train.shape, X_test.shape, y_train.shape, y_test.shape

Out[1]:

((1437, 64), (360, 64), (1437, 10), (360, 10))

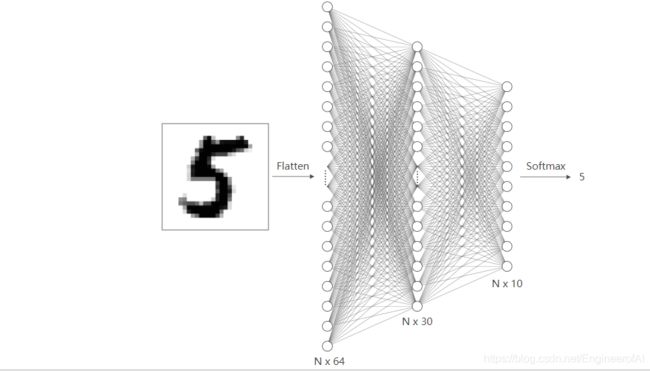
下面，使用 TensorFlow 2 低阶 API 构建一个包含 1 个隐含层的简单神经网络结构。神经网络的输入是单个手写字符样本的向量长度 64，隐含层输入为 30，最终的输出层为 10。

特别地，我们对隐含层进行 RELU 激活，输出层不激活。输出层的单样本长度为 10，这样正好就和上方独热编码后的值对应上了。

In [ ]:

class Model(object):
    def __init__(self):
        self.W1 = tf.Variable(tf.random.normal([64, 30]))  # 随机初始化张量参数
        self.b1 = tf.Variable(tf.random.normal([30]))

        self.W2 = tf.Variable(tf.random.normal([30, 10]))
        self.b2 = tf.Variable(tf.random.normal([10]))

    def __call__(self, x):
        x = tf.cast(x, tf.float32)  # 转换输入数据类型
        # 线性计算 + RELU 激活
        fc1 = tf.nn.relu(tf.add(tf.matmul(x, self.W1), self.b1))
        fc2 = tf.add(tf.matmul(fc1, self.W2), self.b2)
        return fc2

下面，我们开始构建损失函数。损失函数使用 TensorFlow 提供的 tf.nn.softmax_cross_entropy_with_logits，这是一个自带 Softmax 的交叉熵损失函数。最终通过 reduce_mean 求得全局平均损失。

In [ ]:

def loss_fn(model, x, y):
    preds = model(x)
    return tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=preds, labels=y))

于此同时，为了方便查看分类准确度，我们需要手动构建一个准确度评估函数。tf.argmax 可以将 Softmax 结果转换为对应的字符值。然后使用 tf.equal 比对各样本的结果是否正确，最终使用 reduce_mean 求得全部样本的分类准确度。

In [ ]:

def accuracy_fn(logits, labels):
    preds = tf.argmax(logits, axis=1)  # 取值最大的索引，正好对应字符标签
    labels = tf.argmax(labels, axis=1)
    return tf.reduce_mean(tf.cast(tf.equal(preds, labels), tf.float32))

下面开始构建最关键的训练迭代过程。实际上，这部分和构建线性回归非常相似，我们的目的是对神经网络参数进行迭代优化。

In [ ]:

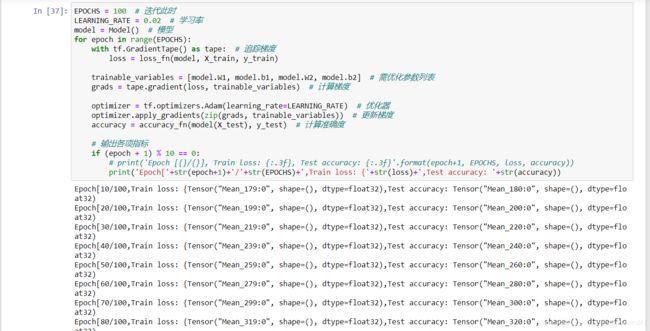
EPOCHS = 100  # 迭代此时
LEARNING_RATE = 0.02  # 学习率
model = Model()  # 模型
for epoch in range(EPOCHS):
    with tf.GradientTape() as tape:  # 追踪梯度
        loss = loss_fn(model, X_train, y_train)

    trainable_variables = [model.W1, model.b1, model.W2, model.b2]  # 需优化参数列表
    grads = tape.gradient(loss, trainable_variables)  # 计算梯度

    optimizer = tf.optimizers.Adam(learning_rate=LEARNING_RATE)  # 优化器
    optimizer.apply_gradients(zip(grads, trainable_variables))  # 更新梯度
    accuracy = accuracy_fn(model(X_test), y_test)  # 计算准确度

    # 输出各项指标
    if (epoch + 1) % 10 == 0:
        print('Epoch [{}/{}], Train loss: {:.3f}, Test accuracy: {:.3f}'
              .format(epoch+1, EPOCHS, loss, accuracy))

Keras 高阶 API 实现

线性回归的实验中，我们使用了 Sequential 序贯模型，实际上 Keras 中更容易理解的是函数式模型。函数式模型最直观的地方在于可以看清楚输入和输出。

函数式模型

例如，下面我们开始定义函数式模型。首先是 Input 层，这在序贯模型中是没有的。然后我们将 inputs 传入 Dense 层，最终再输出。

In [ ]:

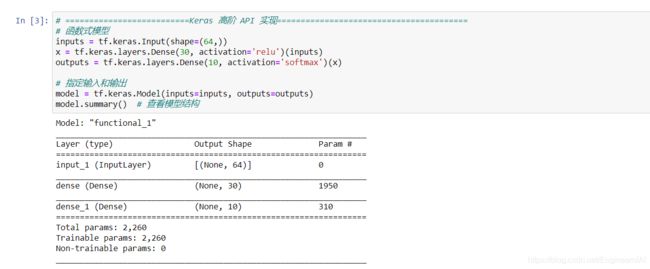
# 函数式模型
inputs = tf.keras.Input(shape=(64,))
x = tf.keras.layers.Dense(30, activation='relu')(inputs)
outputs = tf.keras.layers.Dense(10, activation='softmax')(x)

# 指定输入和输出
model = tf.keras.Model(inputs=inputs, outputs=outputs)
model.summary()  # 查看模型结构

值得注意的是，函数式模型中需要使用 tf.keras.Model 来最终确定输入和输出。

下面，可以开始编译和训练模型。这里使用 tf.optimizers.Adam 作为优化器，tf.losses.categorical_crossentropy 多分类交叉熵作为损失函数。与 tf.nn.softmax_cross_entropy_with_logits 不同的是，tf.losses.categorical_crossentropy 是从 Keras 中演化而来的，其去掉了 Softmax 的过程。而这个过程被我们直接加入到模型的构建中。你可以看到，上面的 model 输出层使用了 softmax 激活。

In [ ]:

# 编译模型
model.compile(optimizer=tf.optimizers.Adam(),
              loss=tf.losses.categorical_crossentropy, metrics=['accuracy'])
# 训练和评估
model.fit(X_train, y_train, batch_size=64, epochs=10,
          validation_data=(X_test, y_test))

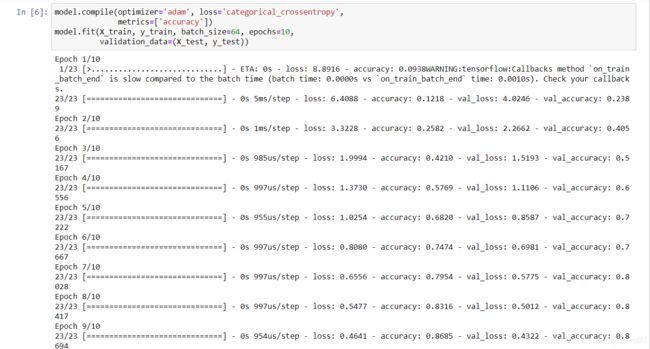
Keras 的训练过程可以采用小批量迭代，直接指定 batch_size 即可。validation_data 可以传入测试数据得到准确度评估结果，非常方便。

序贯模型

当然，上方的函数式模型也可以被写为序贯模型。下面，我们就使用序贯模型进行实现。

In [ ]:

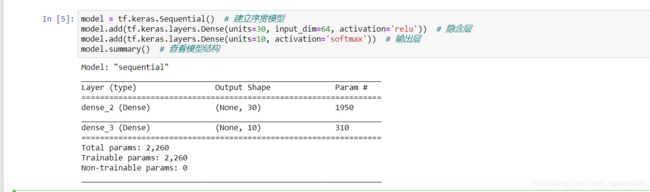
model = tf.keras.Sequential()  # 建立序贯模型
model.add(tf.keras.layers.Dense(units=30, input_dim=64, activation='relu'))  # 隐含层 
model.add(tf.keras.layers.Dense(units=10, activation='softmax'))  # 输出层
model.summary()  # 查看模型结构

此时，我们使用参数简写来替代函数式模型中复杂的写法。

In [ ]:

model.compile(optimizer='adam', loss='categorical_crossentropy',
              metrics=['accuracy'])
model.fit(X_train, y_train, batch_size=64, epochs=10,
          validation_data=(X_test, y_test))

自由度更高的模型

TensorFlow 2 中还支持另外一种更为灵活的 Keras 定义模型方法，这种方法和 PyTorch 中继承 torch.nn.Module 来定义模型的思路非常相似。我们可以继承 tf.keras.Model 来构建模型。这种模型的定义方法自由度更高，我们可以添加更多的中间组件，相对灵活。

In [ ]:

class Model(tf.keras.Model):
    def __init__(self):
        super(Model, self).__init__()
        self.dense_1 = tf.keras.layers.Dense(30, activation='relu')  # 初始化
        self.dense_2 = tf.keras.layers.Dense(10, activation='softmax')

    def call(self, inputs):
        x = self.dense_1(inputs)  # 前向传播过程
        return self.dense_2(x)

接下来的过程和上面相似，实例化模型然后训练并评估。

In [ ]:

model = Model()  # 实例化模型
model.compile(optimizer='adam', loss='categorical_crossentropy',
              metrics=['accuracy'])
model.fit(X_train, y_train, batch_size=64, epochs=10,
          validation_data=(X_test, y_test))

实验总结

本次实验中，我们实验中 TensorFlow 2 构建了简单的前馈神经网络，并完全手写字符识别分类。特别地，一定要掌握 Eager Execution 的实现过程，而对于 TensorFlow Keras 的使用也应用有充分的理解。