PyTorch 学习日记(1)——Tensor与损失函数
Pytorch学习日记(1)
本文中主要讲了Tensor和requires_grad属性以及一些常用的pytorch的损失函数。
1. 配置环境
Python版本:python3.8.2
Torch版本:torch1.4.0
操作系统:Win10
2. 变量
- Tensor
在pytorch中的数据都是封装为Tensor来引用的,Tensor实际上就类似于numpy中的数组,两者可以自由转换。
生成一个(3,4)维度的Tensor:
import torch
x = torch.Tensor(3,4) #这里生成的Tensor是随机的初始值
print("x Tensor:",x)
每一个Tensor都有一个关联torch.Storage,用来存储数据。
3.求导
- requires_grad(旧版本为Variable)
求导的概念
理解pytorch,首先要理解求导的概念。
数学上求导简单来说就是求取方程式相对于输入参数的变化率,也就是加速度,也可以理解为方程式函数的梯度。
求导的作用是用导数对神经网络的权重参数进行调整,注意这里提到了权重参数的概念,这是神经网络的范畴定义了。关于神经网络的基础知识在此不做介绍。
pytorch中为求导提供了专门的class,名称为autograd。如果设置tensor属性requires_grad=True,则tensor会定义两个变量一个是tensor自身的数据即原始权重数据;另一个是grad代表求导后的数据,也就是梯度。每次迭代过程中就是用grad对权重数据进行修正。
在这里我找到了两种方法,创建一个自动计算梯度的Tensor。
(1)第一种创建自动求导Tensor的方法
import torch
x = torch.Tensor(3,4) #这里生成的Tensor是随机的初始值
x.requires_grad_(requires_grad=True)
print(x) # 结果如下图所示
(2) 第二种创建自动求导Tensor的方法
直接创建带有require_grad = True的一个Tensor:
import torch
x = torch.Tensor([1.0,2.0], requires_grade = True) #这里生成的Tensor是随机的初始值
print(x)
(3)第三种创建自动求导Tensor的方法
直接创建带有require_grad = True的一个Tensor:
import torch
x = torch.randn([2,2], requires_grade = True) #这里生成的Tensor是随机的初始值
print(x)
注意:这里只有float类型的Tensor可以计算梯度,如果是int类型系统会报错。
- 求导实践:
import torch
x = torch.ones([2,2],requires_grad=True)
print(x)
y = x+2
z = y * y *3
out = z.mean()
print(z, out)
out.backward() # 反向传播,也就是求导数的意思。输出out对x求导。
print(x.grad) #输出求出的导数,如果是多元素tensor会自动求出每个元素的导数。
解析:4.5是怎么出来的呢?从前面的公式可以看出 z = ( x + 2 ) ∗ ( x + 2 ) ∗ 3 z = (x+2)*(x+2)*3 z=(x+2)∗(x+2)∗3,它的导数是 3 ∗ ( x + 2 ) / 2 3*(x+2)/2 3∗(x+2)/2,当 x = 1 x=1 x=1时导数的值就是 3 ∗ ( 1 + 2 ) / 2 = 4.5 3*(1+2)/2=4.5 3∗(1+2)/2=4.5,和pytorch计算得出的结果是一致的。
权值更新方法:
w e i g h t = w e i g h t + l e a r n i n g _ r a t e ∗ g r a d i e n t weight = weight + learning\_rate *gradient weight=weight+learning_rate∗gradient
learning_rate = 0.01 # learning_rate是学习速率,多数时候叫做lr,又叫学习步长,用步长*导数就是每次权重修正的delta值,lr越大表示学习的速度越快,但是相应的精度会降低,一般设置为0.01.
for f in model.parameters():
f.data.sub_(f.grad.data * learning_rate)
4.损失函数
损失函数,又叫目标函数,是编译一个神经网络模型必须的两个参数之一。另一个必不可少的参数是优化器。
损失函数是指用于计算标签值和预测值之间差异的函数,在机器学习过程中,有多种损失函数可供选择,典型的有距离向量,绝对值向量等等。

上图是一个用来模拟线性方程自动学习的示意图。粗线是真实的线性方程,虚线是迭代过程的示意, w 1 w_1 w1是第一次迭代的权重, w 2 w_2 w2是第二次迭代的权重, w 3 w3 w3是第三次迭代的权重。随着迭代次数的增加,我们的目标是使得 w n w_n wn无限接近真实值。
那么怎么让w无限接近真实值呢?其实这就是损失函数和优化器的作用了。图中1/2/3这三个标签分别是3次迭代过程中预测Y值和真实Y值之间的差值(这里的差值就是损失函数的意思了,当然了,实际应用中存在多种差值计算的公式),这里的差值示意图上是用绝对差来表示的,那么在多维空间时还有平方差,均方差等多种不同的距离计算公式,也就是损失函数了。这里是一维度的方程的情况,扩展到多维度,就是深度学习的本质了。
下面介绍几种常见的损失函数的计算方法,pytorch中定义了很多类型的预定义损失函数,需要用到的时候再学习其他公式也不迟。
我们先定义两个二维数组,然后用不同的损失函数计算其损失值。
4.1 nn.L1Loss

LlLoss计算方法简单,取预测值和真实值的绝对误差的平均数即可。
import torch
import torch.nn as nn
import torch.nn.functional as F
sample = torch.ones([2,2],requires_grad=True)
a = torch.Tensor(2,2)
a[0,0]=0
a[0,1]=1
a[1,0]=2
a[1,1]=3
target = a
criterion = nn.L1Loss()
loss = criterion(sample, target)
print(loss)
最后结果是:1
它的计算逻辑是这样的:
先计算绝对差总和: ∣ 0 − 1 ∣ + ∣ 1 − 1 ∣ + ∣ 2 − 1 ∣ + ∣ 3 − 1 ∣ = 4 |0-1|+|1-1|+|2-1|+|3-1|=4 ∣0−1∣+∣1−1∣+∣2−1∣+∣3−1∣=4
然后再平均: 4 / 4 = 1 4/4=1 4/4=1
4.2 nn.SmoothL1Loss
SmoothL1Loss也叫做Huber Loss,误差在(-1,1)上是平方损失,其他情况是L1损失。

import torch
import torch.nn as nn
import torch.nn.functional as F
sample = torch.ones([2,2],requires_grad=True)
a = torch.Tensor(2,2)
a[0,0]=0
a[0,1]=1
a[1,0]=2
a[1,1]=3
target = a
criterion = nn.SmoothL1Loss()
loss = criterion(sample, target)
print(loss)
4.3 nn.MSELoss
平方损失函数(目前在我认识中,这是我用的最多的一个损失函数)。其计算公式是预测值和真实值之间的平方和的平均数。

代码:
import torch
import torch.nn as nn
import torch.nn.functional as F
sample = torch.ones([2,2],requires_grad=True)
a = torch.Tensor(2,2)
a[0,0]=0
a[0,1]=1
a[1,0]=2
a[1,1]=3
target = a
criterion = nn.MSELoss()
loss = criterion(sample, target)
print(loss)
4.1 nn.BCELoss
二分类用的交叉熵,其计算公式较复杂,这里主要是有个概念即可,一般情况下不会用到。
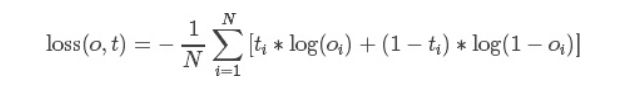
代码:
import torch
import torch.nn as nn
import torch.nn.functional as F
sample = torch.ones([2,2],requires_grad=True)
a = torch.Tensor(2,2)
a[0,0]=0
a[0,1]=1
a[1,0]=2
a[1,1]=3
target = a
criterion = nn.BCELoss()
loss = criterion(sample, target)
print(loss)
4.5 nn.CrossEntropyLoss
交叉熵损失,该公式用的也比较多,比如在图像分类神经网络模型中就常常用到该公式。
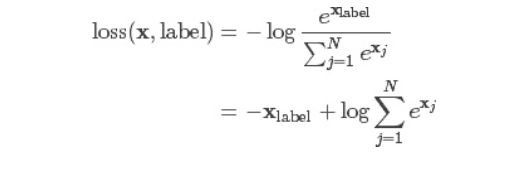
4.6 nn.NLLLoss
负对数似然损失函数(Negative Log Likelihood)

在前面接上一个LogSoftMax 层就等价于交叉熵损失了。注意这里的 x l a b e l xlabel xlabel和上个交叉熵损失里的不一样,这里是经过log运算后的数值。这个损失函数一般也是用在图像识别模型上。
Nn.NLLLoss 和 nn.CrossEntropyLoss 的功能是非常相似的! 通常都是用在多分类模型中,实际应用中我们一般用NLLLoss比较多。
4.7 nn.NLLLoss2d
和上面类似,但是多了几个维度,一般用在图片上。
- input,(N,C,H,W)
- target,(N,H,W)
比如用全卷积网络做分类时,最后图片的每个点都会预测一个类别标签。
本文是作者在学习书籍《Pytorch深度学习实战》一书时做的笔记,pytorch更新部分参考的pytorch官网。