Planning Dynamically Feasible Trajectories for Quadrotors using Safe Flight Corridors in 3-D Complex
在3D复杂环境中，使用安全飞行走廊为无人机规划动力学可行轨迹
[作者] 刘思康、Vijay Kumar
[期刊] IRAL
摘要：
关于使用凸优化导出分段多项式轨迹以控制微分平面系统并应用于微型飞行器 (MAV) 的 3-D 飞行，已有大量文献。 在本文中，我们提出了一种使用安全飞行走廊 (SFC) 概念将轨迹生成公式化为二次规划 (QP) 的方法。 SFC 是一组凸重叠多面体，用于模拟自由空间并提供从机器人到目标位置的连接路径。 我们推导出一种有效的凸分解方法，该方法从使用快速图搜索技术获得的分段线性路径构建 SFC。 SFC 在 QP 中提供了一组线性不等式约束，允许实时运动规划。 由于机器人传感器的范围和视野有限，我们开发了一个receding horizion规划框架，该框架在本地地图的有限足迹内规划轨迹，通过重新规划过程不断更新轨迹。 对于一张大而杂乱的地图，重新规划过程需要 50 到 300 毫秒。 我们展示了我们的方法的可行性、完整性和性能，并在使用四旋翼的模拟和物理实验中应用于高速飞行。
1.引言
在障碍物杂乱的环境中，微型飞行器（MAV）的导航是一个具有挑战性的问题，它不仅需要微型飞行器检测障碍物，还要规划和执行无碰撞和动态可行的轨迹。 在本文中，我们提出了一种算法，可以有效地实时生成这些安全和平滑的轨迹。 我们使用该算法作为四旋翼快速安全导航系统的基础（图 1）。
已经被证明，对于微分平坦系统，轨迹生成问题可以表述为二次规划 (QP) [1]。 轨迹可以参数化为时间上的 k 阶多项式 [2]。 在 [3]-[5] 中使用混合整数方法解决了生成无碰撞轨迹的问题。 由于求解 MILP/MIQP 需要几秒钟到几分钟 [3]-[5]，因此已经开发了其他方法来删除整数变量并求解 QP，这要快得多 [6]-[9]。 轨迹可以以封闭形式求解 [6]，但它需要多次迭代才能生成无碰撞轨迹，尤其是在地图复杂时。 [7] 需要 OctoMap [10] 表示，并在自由空间中生成一系列轴对齐的立方体以生成轨迹。 这种凸自由空间的公式不是通用的，只有当障碍物是长方体时才有效。 在 [11] 中，作者分析了通过障碍物场的高速导航，但他们没有考虑非平凡的机器人动力学，他们的结果可能不适用于 MAV。 [12] 中的框架基于先验路径校正轨迹，但它需要准确的先验地图，这是在未知环境中实际导航的限制。
我们从这些相关工作中汲取了一些想法，并在我们之前的工作 [13]、[9] 的基础上提出了一种强大而有效的解决方案，以实时生成轨迹。 我们的管道使用来自快速图搜索算法的线性分段路径来引导地图的凸分解以找到安全飞行走廊 (SFC)。 SFC 是一组凸连接多面体，用于对地图中的自由空间进行建模，并且可以将其视为 QP 中的线性不等式约束以进行轨迹优化。 受 [14] 的启发，我们开发了一种新的凸分解方法来使用椭球构造 SFC。 使用此管道生成轨迹的总时间足够小，因此我们将其与receding horizion规划 (RHP) 框架一起使用，以构建具有映射和状态估计的导航系统。
我们假设机器人能够通过非线性控制器[15]跟随我们生成的轨迹。 我们通过模拟和真实世界的实验验证了系统在部分感知的复杂环境中避免碰撞的鲁棒性。
为了保证安全，使用了停止策略[13]。 我们算法的三个主要区别优势可以概括为：1）快速计算 2）高速轨迹生成 3）安全性和完整性
与我们之前在[9]中的工作相比，我们提高了规划速度，提出了一种更通用和有效的分解方法，并测试了具有更大行进距离和更高飞行速度的管道。 本文的大纲如下：在第二节中，我们描述了轨迹生成的技术方法； 在第三节中，我们分析了算法的计算开销和效率； 实验结果见第四节； 见解和结论在第五节中。
2.技术概要
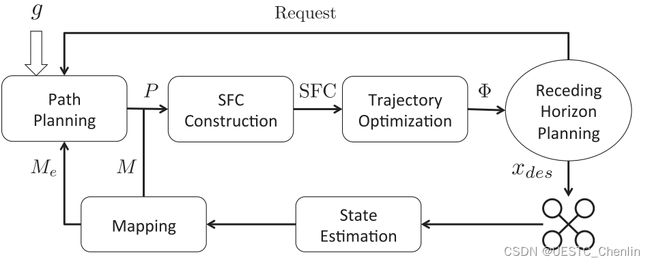
我们的自主系统的整体架构如图 2 所示。在本节中，我们主要讨论前四个组件，通过这些组件我们得出控制 MAV 达到目标的所需轨迹。 快速路径规划和凸分解的源代码已经开源。
图2：我们的自主系统的框图。 我们首先在网格图中找到一条通往目标 g 的有效路径，并在此基础上通过凸分解构造安全飞行走廊 (SFC)。 SFC 内部的轨迹是通过解决优化问题来实现的。 最后，我们能够获得导航四旋翼所需的控制命令。
A.Path Planning
环境被表示为一个占用网格，可以从传感器数据（如激光测距仪、立体相机或 RGB-D 传感器）构建。 然后可以使用图形搜索算法在网格中找到有效的无碰撞路径。 RRT* 和 PRM 等随机方法在概率上是完整的，这意味着如果存在最优路径，但无法保证找到最优路径所需的时间。 此外，当我们需要频繁重新规划时，它们的随机行为使算法的性能变得不可预测。 另一方面，像 Dijkstra 和 A* 这样的基于搜索的算法是resolution完整的，但是当用于大型地图时，它们用于寻找最佳路径的计算时间是一个限制。 Jump Point Search (JPS) [16] 通过在统一成本网格图中进行规划来解决这个问题。 由于我们使用的是 3-D具有统一体素的网格图，JPS 可以应用于我们的问题。 JPS 修剪正在搜索的节点的邻居，并可能将 A* 的运行时间减少一个数量级。 为了将 JPS 与 3-D 体素图一起使用，我们将 [16] 中提出的 2-D 算法扩展到 3-D。 我们提出了 3-D 体素网格的修剪规则，如图 3 和 4 所示。如 [16] 中所定义，自然邻居是指修剪后剩余的节点集。 对于那些由于障碍而无法修剪的邻居，我们称之为强制邻居。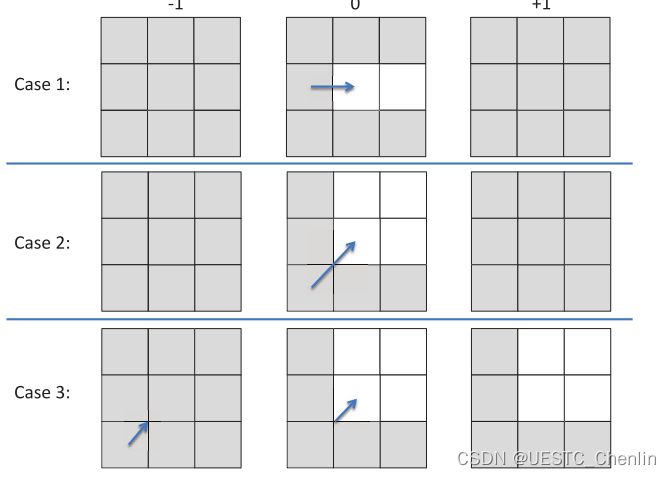 
图 3. 邻居修剪。 我们将 3 × 3 × 3 体素网格绘制为三个 3 × 3 2-D 层——底部 (-1)、中间 (0)、顶部 (+1)。 蓝色箭头指示的中心节点当前正在展开。 当前节点的自然邻居标记为白色。 修剪过的邻居标记为灰色。 蓝色箭头还显示了从其父级的行进方向，其中包括三种情况：（1）。 直，（2）。 二维对角线和 (3)。 3-D 对角线。
图 4. 强制邻居。 当前节点与障碍物（黑色）相邻时，无法修剪突出显示的强制邻居（粉红色）。 红色箭头表示障碍物及其对应的强制邻居对：如果尾部体素被占用，则其头部体素为强制邻居。 例如，在情况 1 中，如果体素 (0, 1, 0) 被占用，则 (1, 1, 0) 是强制邻居。 在案例 2 中，占用的体素 (0, 0, 1) 导致三个强制邻居，在案例 3 中也是如此。为清楚起见，我们省略了相对于蓝色箭头绘制对称情况。
递归修剪和跳跃过程的细节可以在 [16] 中找到。图4中建议的修剪是在检查所有情况和保持算法简单性之间的折衷: 我们添加了更多邻居比需要（三个强制邻居案例），但更容易检查（即更有效）。 JPS 提供与 A* [16] 相同的完整性和最优性保证，唯一的限制是假设统一成本网格适用于我们的案例。 我们的 3-D JPS 显着加快了规划的运行时间（表 1 中的第 6 列），这使得在我们的 RHP 框架内运行轨迹生成成为可能。
B.安全走廊构建
构成障碍物的点集（环境的 3D 网格图表示中的占据体素）表示为 O。自由空间中从起点到终点的分段线性路径 P 记为 P=
为了从 Li 生成凸多面体 Ci，我们描述了两个过程：（1）“Find Ellipsoid”，首先拟合 Li 周围的椭球；（2）“Find Polyhedron”，从切平面构造多面体 Ci 膨胀的椭球序列。 为了减少计算时间，我们添加了一个边界框来限制我们考虑障碍物的 Li 周围的空间。 此外，我们提出了一个收缩过程来保证非点机器人是无碰撞的。 在以下小节中，我们将介绍这些程序的详细信息。 为简单起见，我们删除了下标“i”并简单地使用 L,C 来表示相应的线段和多面体。
1）Step1-Find Ellipsoid：在这一步中，我们找到一个包含线段 L 并且不包含 O 的任何障碍点的椭球。一个椭球被描述为
对于 R3 中的椭球，E 是一个 3 × 3 对称正定矩阵，表示球体的变形(¯p≤1)。 E 可以分解为 E = R^TSR 其中 R 是将椭球轴与地图轴对齐的旋转矩阵， S = diag(a, b, c) 是对角尺度矩阵，其对角元素代表椭球半轴的相应长度 . d 表示椭球的中心。 不失一般性，我们假设a≥b，a≥c。 我们的目标是在给定线段 L 和障碍物 O 的情况下找到 E, d。
这个椭球分两步计算：首先，我们收缩一个初始球体以导出最大椭球体（一个具有两个等长轴的椭球体）； 其次，我们沿着第三轴“拉伸”这个球体以获得最终的椭球体。 在第一步中，初始椭球是以L的中点为中心，直径等于L的长度的球体。假设椭球的~x轴的长度固定并与L对齐，我们减少其他两个轴的长度 ，直到球体不包含障碍物。 这是通过从 ξ 的中心搜索 O 中最近的障碍物来完成的。 图 6 从二维角度显示了收缩过程。
图6.收缩椭球 粗实线段为L，灰色区域表示障碍物，而白色区域为自由空间。左：从一个球体开始，我们找到最接近L中心的点p，并调整短轴的长度，使虚线椭球接触到这个p。中：重复相同的步骤，找到新的最近点p和新的椭球体。右：椭球内无障碍物，当前椭球为最大椭球。需要几次迭代以确保最终球体排除所有障碍。
在p*点接触到障碍物的最大椭球体，伴随着线段L，定义xy平面的最大椭球体。随着，我们拉伸椭球z轴的长度，使得与a相等，去形成一个新的初始椭球。c的实际值由利用类似图6的过程找到另一个最近点来决定。
2） Step 2 – Find Polyhedron: 将上一步中找到的椭球表示为 ξ0，它在 pc 0 = p∗ 处接触障碍点。 此时椭球的切平面创建一个半空间 
，包含椭球体。 在计算 H0 之后，我们移除 O 中位于 H0 之外的所有障碍物（称为剩余障碍物集合 Oremain），并“扩张”椭球（保持其纵横比不变）直到它与另一个障碍点接触， pc 1，此时新的椭球称为 ξ1，新的切线超平面创建一个新的半空间 H1。 继续该过程以获得半空间序列H0，H1，···，Hm。 这些 m +1 个半空间的交集给出了凸多面体，
，其中 aj 和 bj 分别是矩阵 A 的第 j 列和向量 b 的第j个元素。
图 7 显示了一个椭圆体扩张的示例。 在每次扩张迭代中，椭球 ξj 在定义第 j 个半空间 Hj 的点 pc 处接触障碍物，Hj 是 ξj 在 pc j 处的切线。 算法 1 显示了伪代码。 第j个半空间Hj，是 ξj 在 pc 处的切平面。被计算为：
图7：扩张椭球 ξ0 以找到半空间。 左：找到 ξ0 和超平面（红线）的第一个交点 pc 0，相应的半空间 H0 之外的障碍点被移除（阴影）。 中：找到下一个交点 pc 1 （虚线椭球表示原始椭球 ξ0，实线椭球表示新椭球 ξ1），继续从地图中移除新半空间之外的障碍点。 右：保持扩张直到当前地图中没有障碍物，凸空间C（蓝色区域）由半平面的交点定义。
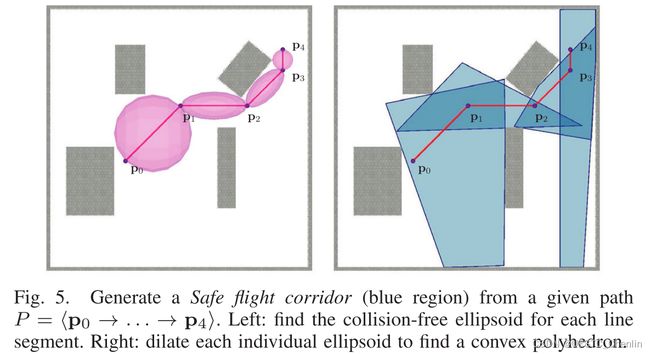
到目前为止，给定障碍物O，我们能够为L生成多面体C。我们在路径P的每个单独线段上应用此方法，以获得安全飞行走廊为SFC(P)= {Ci | i = 0,1，...，n − 1} (图5)。由于原始椭球在对应的多面体内部，因此我们保证线段L也在多面体内部。因此，保证整个路径P在SFC(P) 内。
3）：边界框：如所示，该算法需要搜索O中至少两次中的所有点，以检查每个线段L构造多面体C时与膨胀的椭圆形相交。这是一个昂贵的过程。 我们通过在L周围添加一个边界框来减少要检查的点数，因此仅搜索其中的障碍物。 此过程节省了大量的计算时间，还可以防止轨迹离原始路径太远。 L的边界框由6个矩形组成，使边界框的轴与L对齐，并且从每个框到L的最小距离为rs。 如果MAV 的最大速度和加速度为 vmax,amax，施加的条件是安全半径
，图 8 显示了应用边界框的典型结果。 生成的 SFC 包含类似的半空间，如图 5 所示。
图8：左：在具有安全半径 rs 的每个线段上应用边界框。 右图：膨胀单个线段以找到凸多面体。 与图 5 相比，我们只处理相应边界框内的障碍物。
4） 收缩：我们将机器人建模为半径为Rr 的球体，并在原始地图 M 中扩展占用的体素以生成配置空间 Me，以便我们能够将机器人视为单点进行规划。 在为 Me 中规划的路径 P 构建 SFC 时，使用 Me 可以生成窄椭圆体和多面体（图 9(a)-9(b)）。 为了避免这种糟糕的SFC，我们使用原始地图M来生成SFC，并将SFC缩小机器人半径Rr，以保证安全。 通过将每个支持超平面沿其法线推Rr 来应用收缩过程。 当我们将障碍物与每个超平面之间的距离增加Rr 时，此过程可确保缩小的 SFC 的安全性，但也可能会排除可能导致安全飞行走廊不连续的路径的某些部分（图 9d）。 为了保证连续性，我们必须确保线段 L 在收缩的多面体 C 内。 为此，我们修改算法 1：对于任何半空间 Hj ∈ C（C 是原始多面体），我们检查从 L 到 Hj 的超平面的最小距离 d(L,Hj)。如果 d(L,Hj) < Rr，我们调整超平面的法线使得 d(L,H j)= Rr （H j 是调整后的半空间）。 新半空间 Hj 的超平面也通过 Hj 与膨胀椭球的交点（图 9(e)）。
图9：通过收缩过程构建SFC（P）。 为清楚起见，我们使用黑色粗线绘制扩展地图 Me 的轮廓。 SFC 的轮廓由蓝色边界表示，而缩小的 SFC 被绘制为内部的蓝色区域。 (a) 和 (b) 中的 SFC 是使用 Me 导出的，没有收缩。 几个椭球体和相应的多面体相当窄。 在 (c) 和 (d) 中，SFC 是使用原始地图 M 生成的，因此与 (a) 和 (b) 相比，走廊“更宽”。 由于该 SFC 还穿透了扩展地图中的障碍物，因此我们将其缩小机器人半径Rr 以得出“安全”SFC。 但是，这种收缩过程可能会导致 SFC 中的不连续性，例如 p2（圆圈）在 (d) 中线段 p1 → p2 生成的收缩多面体之外。 在（e）中，绿色超平面被调整，使得 p2 仍然在缩小的多面体内部。
C.轨迹优化
在本节中，我们将介绍使用生成的 SFC 生成最小sanp轨迹的方法。 我们在以前的工作中采用了类似的轨迹优化公式[9]。 假设SFC包含N个凸多面体，整个轨迹由N多项式组成，第i-th多项式位于第i个多面体CI内部。 因此，可以将最小snap轨迹的凸优化作为QP形成，并以机器人的启动和结束状态限制为
其中矩阵Ai,bi对应第i个多面体Ci。轨迹组成：
在这里，我们使用分段多项式作为 [17] 来描述轨迹 Φ(t)。 因此，
表示在时间 t 的所需位置、速度、加速度和加加速度，它们是非线性控制器的输入 [15] 计算控制四旋翼所需的力和动量。 上式中的 Δti 是指每个多项式的时间，Δti = ti+1-ti。 图 10 显示了由 SFC 限制的分段多项式轨迹的示例。
图 10. 示例轨迹具有三个多面体 Ci，每个段 Φi 被限制在其对应的多面体内。 红色的起点和终点被限制在这些位置，黄色的结点仅被限制为连续的，并且允许在相邻多面体对的交点内变化。
Δti 或时间分配的估计会显著影响生成的轨迹。 由于每个 SFC 都包含一个有效路径 P，简单的时间分配方法是使用梯形速度分布将该 P 映射到时域。 使用初始时间分配求解方程 3 可能导致轨迹具有超过 MAV 的最大阈值的大速度、加速度或加加速度。 与 [6] 类似，我们根据等式 5 修改 Δti 以调整时间分配，以便机器人可以遵循使用 Δt i 生成的最终轨迹。 将生成轨迹的最大速度、加速度和加加速度表示为 vmax,amax,jmax，将相应的阈值表示为 ¯vmax, ¯amax, ¯jmax。 单元 1 用于防止修改适当的时间分配。
在优化过程中，我们使用一种基于样本的方法来限定每一个多项式，具体细节在[2]中可以找到。此外，我们始终假设速度、加速度和加加速度为零的静态最终状态，以确保飞行安全。
D.receding horizion planning
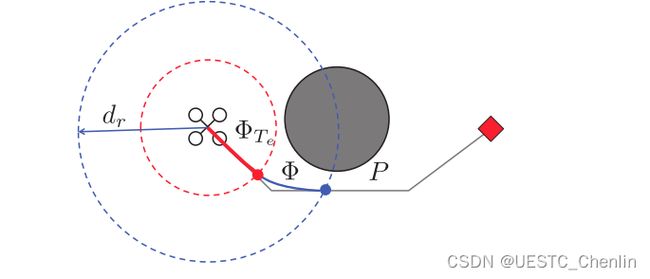
为了在未知环境中通过局部传感导航 MAV，我们使用 Receding Horizon Planning (RHP) 不断生成轨迹，直到机器人到达最终目标。 如 I节所述，RHP 是 Receding Horizon Control 的一种变体，人们在其中解决一个固定的未来时间间隔内的最优控制问题 [18]，[19]。 我们没有解决固定的时间间隔，而是将规划范围定义为在我们的后退范围框架中受感测范围限制的最长距离 dr。 一旦我们规划了一条从起点到目标的路径，我们只使用该路径的一部分以机器人的半径为 dr 来生成轨迹 Φ。 机器人只在很短的时间内执行Φ，我们称之为执行范围Te，因此下一个重新规划时期的轨迹生成的起始状态由Φ（Te）确定。 我们选择 Te 以保证生成轨迹的时间小于 Te，以便机器人在完成当前轨迹 Φ 的执行后能够遵循新的轨迹。 换句话说，当机器人在当前 epoch 执行轨迹时，我们开始为下一个 epoch 生成轨迹。 由于执行时间 Te 大于生成轨迹所需的时间，因此机器人在执行完当前轨迹后总是能够过渡以跟踪新轨迹。 图 11 显示了 RHP 的示例。
图 11. receding horizion规划。 规划路径 P 直接到达目标（红色菱形）。 然而，为了生成轨迹Φ，我们只根据规划范围dr规划到边界点。 根据执行范围 Te，执行轨迹 Φ(Te) 以红色圆圈为界。
在某些情况下，如果规划器无法找到路径或由于时间分配不当导致轨迹优化失败，则无法实现下一个重新规划时期的轨迹。 我们利用[13]中描述的停止策略使机器人在故障发生时停止，并且在机器人自身稳定后，我们继续寻找新的轨迹，使用相同的轨迹生成方法。 我们能够在全局或局部地图中规划轨迹，但对于我们的实验，我们使用局部地图。 使用最后几个传感器读数构建局部地图，而全局地图需要完整的 SLAM 解决方案来纠正状态估计中的漂移。 与全局地图相比，局部地图更容易实现并且足以避障，但缺乏全局信息使得规划器全局不完整并且容易受到类似死胡同的环境的影响。
3.分析
A.与IRIS对比
用于生成无碰撞凸区域 [5]、[14] 的现有算法需要正确选择种子和障碍物的几何表示，这很难从真实的传感器数据中获得。 在他们的过程（IRIS）中，通过凸优化求解最大椭球需要很长时间。 对于图 12 所示的地图，IRIS 算法大约需要 110 毫秒，而我们的算法只需要 4.8 毫秒。 事实上，在 IRIS 中选择用于生长椭球的种子并非易事，这也使得实时运行 IRIS 进行分解变得更加困难。
图12。将我们的凸分解方法与IRIS进行比较。红星指出了开始和目标。即使使用两个不同的安全飞行走廊，生成的轨迹也非常相似。垂直于轨迹的浅蓝色短线显示相应位置的速度。
B.运行时间分析
我们使用四种不同的地图通过生成数百条轨迹来测试算法的运行时间。 这四张地图被命名为“随机块”、“多层”、“森林”和“户外建筑”。 我们在每张地图中以一定的密度对目标进行采样，并手动选择一个起点。 图 13 显示了这些映射和生成的结果。 选择这些地图是因为它们对于现实世界中遇到的不同环境是典型的（即 2.5-D、完全 3-D、随机分散的复杂障碍物和现实世界数据）。
为了评估我们算法的计算开销，我们将整个轨迹生成分为三个部分：路径规划、凸分解和轨迹优化。 表 1 显示了在 i7-4800MQ 处理器上生成轨迹时每个组件的时间成本，如图 13 所示。 对于路径规划，我们比较了两种不同的方法：A* 和 JPS，以显示使用 JPS 对运行时间的影响。 从结果可以看出，我们能够在几百毫秒内生成轨迹，这对于以 2-3 Hz 的频率重新规划来说已经足够快了。
C.完备性
在本小节中，我们将讨论局部地图中的算法完整性：如果存在达到地图分辨率的轨迹，是否会找到轨迹。 由于 SFC 的构建是从线段开始的，因此它至少会产生一组包含这些线段的凸区域。 在这种情况下，优化的可行集总是包含轨迹 Φ 是具有静态开始和结束状态的多项式的解。 对于初始非静态动力学导致轨迹优化失败的其他情况，车辆将遵循现有的无碰撞轨迹或执行停止策略。 最终，车辆将以悬停模式停止，如果存在通往最终目标的路径，我们始终可以从该静态状态生成轨迹。 总之，我们的算法是完整的，因为我们使用的路径规划算法是完整的。 使用全局地图时（例如，图 13），可以保证完整性。 但是，如果我们只有局部地图，则无法实现全局完整性，机器人可能会陷入死胡同。
图 13. 在不同地图中生成从起点（大红球）到采样目标（小红球）的轨迹。 蓝色曲线是生成的轨迹，青色区域是重叠的 SFC。
D.飞行速度
在本节，我们通过无量纲参数方式分析了飞行速度。 我们通过最大加速度¯amax（受车辆推重比约束）和最大速度¯vmax（受空气阻力限制）来描述 MAV 模型。 这两个参数反映了四旋翼飞行器的飞行速度。 对于不同的平台，由于硬件配置不同，我们通常有不同的¯amax、¯vmax 值。 规划地平线dr（受感测范围限制）和执行地平线Te（受机载计算能力限制）是RHP中影响飞行器飞行速度的两个独立变量。 它们可以通过归一化无量纲化为
可以使用两个参数来评估飞行速度：达到目标的总时间 T 和最大速度 vmax。 假设总距离为 dgoal，我们可以使用以下符号来评估标称飞行时间和最大速度：
我们使用这些无量纲参数绘制了在模拟中使用三个不同机器人的测试结果（图 14）。 我们可以得出结论，可以通过设定一个大的计划范围来实现快速飞行。 但在实际实验中，规划视野受限于感应范围，达到一定阈值后不会增加飞行速度。 执行范围也受到板载计算的限制，例如在表 1 中，重新计划的最大时间成本高达 0.47 秒，这为 Te 设置了下限。
图 14. 保持 te 固定为 0.1 并改变 l 的 3 个不同四旋翼的无量纲分析：对于机器人 1，¯vmax =20m/s，¯amax =10m/s2； 对于机器人 2，¯vmax =10m/s，¯amax =5m/s2； 对于机器人 3，¯vmax = 5m/s，¯amax = 5m/s2。 到达目标的总时间 τ 和最大速度 u 随着 l 的增加而变为 1.1（由于我们使用基于样本的方法进行轨迹优化，最大速度会稍微超出实际界限），这意味着更长的时间 规划视野导致更快的飞行。
为了测试高速避障，我们通过在一个区域内随机散布 N 个凸面障碍物来模拟环境。 典型环境如图 15 所示。使用 40m 感应范围的仿真 Velodyne Puck VLP-16，机器人能够在这片森林中达到 19.2m/s 的最高速度，并在 14.3s 内到达 200m 外的目标。
图 15. 400 棵树被随机放置在一个 200×40m 的正方形上。 RHP 规划范围为 50m，执行范围为 1s。 蓝色曲线显示了机器人从一端到另一端的轨迹。 绿点显示每个重新计划的开始位置。
4.实验结果
我们在图 1 所示的四旋翼平台上应用建议的导航管道。我们使用 MSCKF 算法 [20] 的立体版本进行状态估计，并使用 Velodyne VLP-16 来构建局部地图。 所有计算均在板载英特尔 NUC 计算机（双核 i7）上执行。 图 17 显示了室外场景中的几个实验，其中机器人对环境的先验知识为零。 给定一个相对于初始机器人位置的目标，我们的系统可以成功到达目标并返回而不会碰到任何障碍物。 对于图 17 所示的运行，车辆以高达 5m/s 的速度行驶。在测试 1 中，机器人成功地避开了具有复杂 3-D 几何形状的树木和灌木丛。 在测试 2 中，由于森林茂密，机器人决定绕着它飞行而不是飞过它。 在测试3中，机器人避开树木、森林和建筑物，机器人行驶的总距离约为1km。 我们的轨迹是平滑的，并受速度、加速度和加加速度阈值的限制，这有助于减少基于视觉的状态估计的误差：回到起始位置后的一般位置漂移小于 1%。
图 16. 在实验1中的状态估计vs 期望命令 . 实际机器人状态标记为蓝色，而所需命令标记为黑色。
图 17. 户外实验。 网格单元尺寸为 10m × 10m。 最大速度设置为 5m/s，同时我们也将最大加速度限制为 3m/s2。 二维轴显示 x - y 轴的方向，原点位于标记为由 S 表示的读取星的起点处。
由于我们将最大加速度设置为相对较小（3m/s2），机器人能够密切跟踪生成的轨迹。 图 16 显示了控制器在测试 1 期间的性能，我们可以看到位置误差小于 0.2m。
5.总结
高速自主导航对 MAV 来说是一个挑战，因为 (a) 必须将动力学约束纳入运动规划； (b) 用于规划的计算资源有限； (c) 有限的传感器感应范围，因此机器人只能访问局部的世界地图。 在本文中，我们描述了一种轨迹生成算法，该算法仅基于机载传感和计算实时推导动态可行、无碰撞轨迹，并在receding horizion规划。 我们研究了速度和安全性之间的权衡以及诸如（a）Te，执行范围，（b）l，不同四旋翼环境中的传感器感应范围等参数的影响。 这对整个系统的研究和子系统之间的平衡将确定阻碍航行速度的限制因素，并指导未来的研究以调解这些因素。