k邻近算法原理和sklearn函数的参数详解
k k kNN
k近邻(k-Nearest Neighbor, kNN),kNN的一个特点是没有显式的训练过程,事实上,它是“懒惰学习”(lazy learning)的代表,那些在训练过程中就迫不及待学习处理样本的方法,称为“急切学习”(eager learning)。
讨论最近邻算法(k=1)
给定测试样本x,若其最近邻样本为z,则最近邻分类器出错的概率就是x和z类别标记不同的概率
P ( e r r ) = 1 − ∑ c ∈ Y P ( c ∣ x ) P ( c ∣ z ) P(err)=1-\sum_{c\in \mathcal{Y}}P(c|x)P(c|z) P(err)=1−c∈Y∑P(c∣x)P(c∣z)
假设样本独立同分布,且对任意 x x x和任意小正数 δ \delta δ,在 x x x附近 δ \delta δ距离范围内总能找到一个训练样本;换言之,对任意测试样本,总能在任意近的范围内找到上式中的训练样本 z z z。令 c ∗ = a r g m a x c ∈ Y P ( c ∣ x ) c^{*}=\underset{c\in \mathcal{Y}}{argmax}P(c|x) c∗=c∈YargmaxP(c∣x)表示贝叶斯最优分类器的结果,有
P ( e r r ) = 1 − ∑ c ∈ Y P ( c ∣ x ) P ( c ∣ z ) ≃ 1 − ∑ c ∈ Y P 2 ( c ∣ x ) ≤ 1 − P 2 ( c ∗ ∣ x ) = ( 1 + P ( c ∗ ∣ x ) ) ( 1 − P ( c ∗ ∣ x ) ) ≤ 2 ∗ ( 1 − P ( c ∗ ∣ x ) ) \begin{aligned} P(err) &= 1-\sum_{c\in \mathcal{Y}}P(c|x)P(c|z) \\ &\simeq 1-\sum_{c\in \mathcal{Y}}P^2(c|x) \\ & \le 1 - P^2(c^*|x) \\ &=(1+P(c^*|x))(1-P(c^*|x)) \\ & \le 2*(1-P(c^*|x)) \end{aligned} P(err)=1−c∈Y∑P(c∣x)P(c∣z)≃1−c∈Y∑P2(c∣x)≤1−P2(c∗∣x)=(1+P(c∗∣x))(1−P(c∗∣x))≤2∗(1−P(c∗∣x))
于是我们得到了一个令人惊讶的结论:最近邻分类器虽然简单,但它的泛化错误率不超过贝叶斯最优分类器的错误率的两倍。emmm ,不知道自己学了个啥
k值的选择
显然k的选择决定了这个模型的性能,如果k值较小,这个模型就较为复杂,容易发生过拟合,如果k=N,无论输入的实例是什么,输出预测都是这N个样本中的最多的类。
k k k邻近法的实现-kd树
当数据量较小时,我们可以针对每一个测试样本来遍历整个训练集计算哪个离它最近,但当数据量较大时计算机就做不到了,这个时候要用一些快速搜索定位的方法。
kd树是二叉树的一种,是对k维空间的一种分割,不断地用垂直于坐标轴的超平面将k维空间切分,形成k维超矩形区域,kd树的每一个结点对应于一个k维超矩形区域。
注意:这里的k维的k表示的是数据的维度,上文中 x i = ( x i 1 , x i 2 , ⋯ , x i m ) x_i =(x^1_i, x^2_i, \cdots, x^m_i) xi=(xi1,xi2,⋯,xim)**我们称 x i x_i xi为m维数据。(不要理解为K 个训练点的K,你看我甚至把训练点的K大写,维度的k小写 )
kd树的构造
首先我们需要构造kd数,构造方法如下:
- 选取为 x ( 1 ) x^{(1)} x(1)坐标轴,以训练集中的所有数据坐标中 x ( 1 ) x^{(1)} x(1)的中位数作为切分点,将超矩形区域切割成两个子区域。将该切分点作为根结点,由根结点生出深度为1的左右子结点,左节点对应坐标 x ( 1 ) x^{(1)} x(1)小于切分点,右结点对应坐标 x ( 1 ) x^{(1)} x(1)大于切分点
- 对深度为 j j j的结点,选择为切分 x ( l ) x^{(l)} x(l)坐标轴, l = ( j m o d k ) + 1 l=(j\mod k)+1 l=(jmodk)+1,以该结点区域中训练数据 x ( l ) x^{(l)} x(l)坐标的中位数作为切分点,将区域分为两个子区域,且生成深度为 j + 1 j+1 j+1的左、右子结点。左节点对应 x ( l ) x^{(l)} x(l)坐标小于切分点,右结点对应 x ( l ) x^{(l)} x(l)坐标大于切分点
- 重复2,直到两个子区域没有数据时停止。
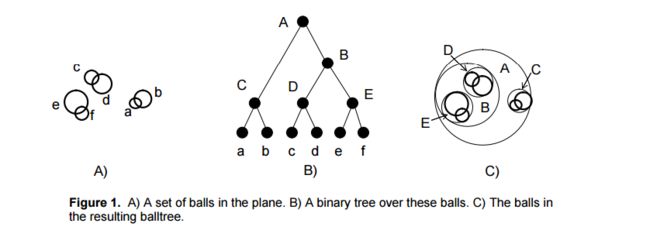
另一种实现方式-Ball树
原理:为了改进KDtree的二叉树树形结构,并且沿着笛卡尔坐标进行划分的低效率,ball tree将在一系列嵌套的超球体上分割数据。也就是说:使用超球面而不是超矩形划分区域。虽然在构建数据结构的花费上大过于KDtree,但是在高维甚至很高维的数据上都表现的很高效。
balltree构建方式
空间中散落着很多个点。
- 把整个空间当作一个大簇。
- 找到距离最远的两个点 a 和 b, 叫做观测点(请记住, 最后面要考) , 以它们为种子。
- 其余的簇内点 s 分别计算与 a 和 b 的距离, 离 a 近就归到 a 的子簇, 对 b 同理。
- 该找圆心和半径了, 这涉及另一个问题: 给一堆点, 怎么找到最小半径和圆心?最小圆覆盖问题.贴个链接: 最小圆覆盖问题算法
用它解出的圆不会超出父类圆的范围, 如果超出了会增加不少麻烦, 因为超出部分必没有属于该簇的点, 还容易在搜索时被干扰, 增加搜索量.
回头看ball tree的数据结构, 发现: 因为求最小圆要随机打乱簇内点保证复杂度, 所以permutation可能是用于暂存打乱点的。 - 上一步画好了圆, 就可以根据它们再分. 分别以两个圆重复1~4步, 直到只剩一个点, 就作为叶节点存储下来。
利用balltree搜索点的方式
当点在balltree中的情况:搜索方法和kd树类似
当点不在balltree的情况:
这时可以借助每个簇中必有的点:观测点,每个簇都有两个观测点, 分别属于两个子簇. 它在一定程度上反映了当前簇的位置,如果我每次取簇的两个观测点, 然后每次选择离得比较近的观测点所在的子簇, 到最后会获得一个距离上不是最近但也差不多的点,这样我就可以以它为上界画圆, 再走一遍balltree.我的代价就是跑了两次tree。
sklearn中的k邻近
class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)
参数:
n_neighbors:int型,默认为5。即k值。
weights: {‘uniform’, ‘distance’} or callable, default=’uniform’ ,邻居们标签的权重。
algorithm:{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, default=’auto’,搜索邻居的算法。
leaf_size:int, default=30,叶节点数量,如上所述, 对于小样本暴力搜索是比基于树的搜索更有效的方法. 这一事实在 ball 树和 KD 树中被解释为在叶节点内部切换到暴力搜索。
p:int, default=2,距离,当p=1时是曼哈顿距离,当p=2时是欧氏距离。
metric:str 或 callable, default=‘minkowski’,用于树的距离度量。默认度量是 minkowski,并且 p=2 等效于标准欧几里得度量。也可以自己编写距离函数。
metric_param:dict,默认值=None,距离度量的其他参数。
n_jobs:int,默认=无,工作cpu的个数。
属性:
classes_:shape为(n_classes,),分类器读取到的类标签。
effective_metric_:str or callble,使用的距离度量。
effective_metric_params_:dict,使用其他的距离度量的参数。
n_features_in_:int,Number of features seen during fit.
feature_names_in_ ndarray of shape (n_features_in_,),上面的用到的name
n_samples_fit_: int,Number of samples in the fitted data.
output_2d_:bool,当y的形状为 (n_samples, ) 或 (n_samples, 1) 时为 False,否则为 True。
参考文档(https://sklearn.apachecn.org/docs/master/7.html)
,当y的形状为 (n_samples, ) 或 (n_samples, 1) 时为 False,否则为 True。
参考文档(https://sklearn.apachecn.org/docs/master/7.html)