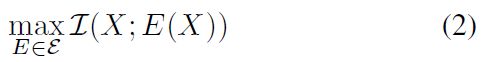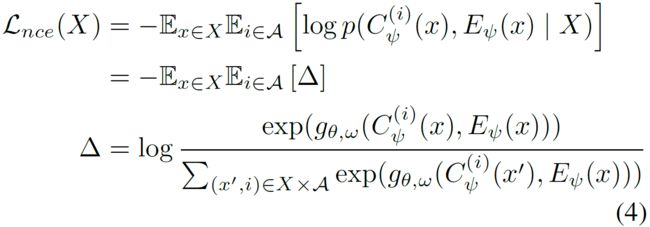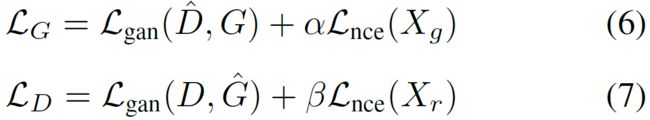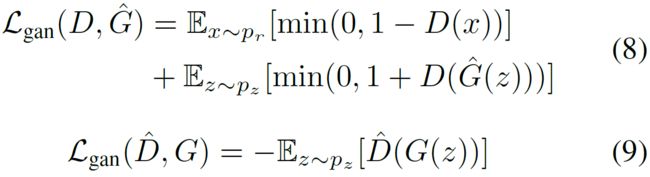InfoMax-GAN: 通过信息最大化（Information Maximization）和对比学习（Contrastive Learning）改进对抗（Adversarial）图像生成

目录

0. 摘要

1. 介绍

2. 背景

3. InfoMax-GAN

3.1 框架

3.2 Contrastive Loss

3.3 缓解Catastrophic Forgetting

3.4 缓解Mode Collapse

4. Experiment

4.1 Experiment Settings

4.2 生成性能评估

4.3 Training Stability

4.4 低计算量

4.5 消融实验（Ablation Studies）

5. 补充：谱归一化（spectral normalization）

5.1 理论依据

5.2 算法

6. 参考

---

InfoMax-GAN: Improved Adversarial Image Generation via Information Maximization and Contrastive Lear

0. 摘要

虽然生成对抗网络（Generative Adversarial Networks，GANs） 是很多生成模型（generative model）的基础，但仍面临很多问题。本文，作者提出了一个原则框架（principled framework）来同时缓解GAN的两个基础问题：鉴别器（discriminator）的遗忘（catastrophic forgetting）和生成器（generator）的模式坍塌（mode collapse）。实现办法：为GAN加入对比学习和互信息最大化的方法，并通过广泛分析理解（extensive analyses）性能提升的原因。相比于最新的的研究，本方法极大地稳定了GAN的训练，提升了GAN生成图像的性能。特别地，在图像域（例如：人脸），相比于最新的SSGAN，本方法有更好的性能。本方法是实用且易于实现的：它只涉及一个辅助目标，计算量低，在大量的训练设置和数据集上性能稳定良好且没有任何的超参数调试（hyperparameter tuning）。

1. 介绍

GAN是一种生成模型，知名于生成高保真（high-fidelity）数据的采样效率（sampling efficiency）。GAN由两个模块组成：鉴别器（discriminator）和生成器（generator）。

其中，V是输出值，是先验噪声分布，是真是数据分布，是通过采样随机噪声z生成的数据。

用生成器和鉴别器各自的误差函数（loss function）训练他们等价于最小化真实分布于生成数据分布的JS散度（Jensen-Shannon divergence）。然而，GAN的训练是有名的难。首先，该理论的基础假设是discriminator被训练到最优，这在实践中可能导致梯度饱和（saturating gradients）。即使如此，也不能保证优化结果的收敛（convergence）。因为discriminator和generator独立同时地在高维空间进行优化。最后，GAN面临mode collapse的问题，即生成数据的分布只能拟合真实分布的一部分模式，从而导致生成样本有限的多样性。因此，近些年许多研究想要解决这个问题。

GAN训练不稳定的主要原因是动态的训练环境：随着生成器的学习，鉴别器面对的模型分布在不断变化。因为GAN是神经网络，鉴别器容易遗忘：在训练过程中，随着网络参数的更新，网络只关注当前的task而遗忘之前的task，这也导致了训练的不稳定性。最新的Self-supervised GAN（SSGAN），提出了可以缓解鉴别器遗忘的方法，从而提升了训练稳定性。然而，该方法不能解决模式坍塌。并且在图像域（例如：人脸）是失败的。此外，SSGAN虽然能缓解鉴别器遗忘，但是促进了生成器的模式坍塌。

为了解决这些问题，作者提出了同时缓解遗忘和模式坍塌的方法。在鉴别器端，通过最大化互信息来改进长期representation学习，从而减少动态训练环境中的遗忘。在生成器端，用对比学习促使生成器产生不同的图像（生成区别明显的正/负例），从而解决模式坍塌。

2. 背景

这是最大化互信息的目标函数。其中，X为输入，E是编码器，用于提取X中最重要的特征。是一些函数类别。最大化该函数等价于最大化，其中，和是架构相同的编码器。最大化等价于最大化InfoMax目标函数的下界：

最大化有如下优点：

• 使用不同的编码器可以获得数据不同的视角和模态，从而提升模型的灵活性。
• 相比于原始数据，编码数据位于更低维的隐空间（latent space），从而减少计算限制

最新的无监督展示（representation）学习是用对比的方法，最大化局部特征与全局特征的互信息。然而直接最大化互信息通常不可行，所以通常用最大化InfoNCE下边界的方式代替：基于评判（critic）找到使一个正例，该正例与负例集合的对比损失最小。这些正反例通过匹配特征、数据增强（augmentation）或者它们的结合来随意生成。本文的方法也是最大化InfoNCE的下界，且与Deep InfoNCE（用局部和全局特征进行最大化）更为相似。   

3. InfoMax-GAN

3.1 框架

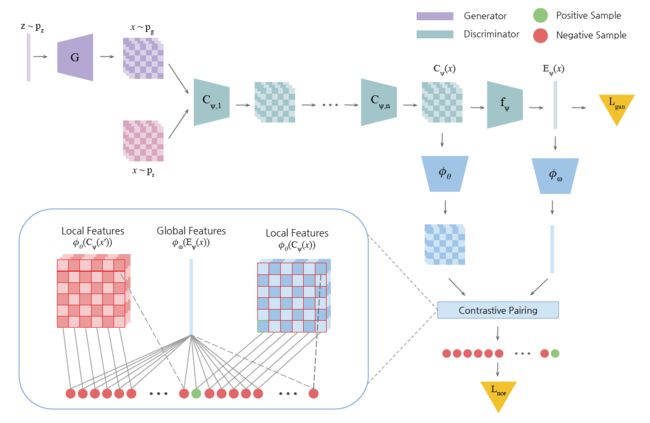
下图是InfoMax-GAN的框架。

首先最大化的下界。​表示鉴别器中生成全局特征的layers。表示生成局部特征的layers。是n个中层鉴别器，是之后把局部特转化为全局特征的layers，最终用于计算GAN的目标函数。局部特征和全局特征分别是鉴别器的编码器的倒数第二和最终输出特征。

下一步，局部特征和全局特征被送入critic network 和，并被投影到RKHS（Reproducing Kernel Hilbert Space），从而获取局部和全局特征的相似性。这些投影后的特征经由对比匹配（Contrastive Pairing）获得正例和负例。给定图像x，通过匹配投影的全局特征向量与投影的局部向量之一来获得正例，其中是个局部特征的索引。因此，正例样本可表示为。相对于每一个正例，负例源于同一mini-batch的另一个图片，表示为。仅第一项有差别是为了最大化全局特征与同一图像的局部特征，而不是其他图像的局部特征。

3.2 Contrastive Loss

对mini-batch中的N个图像，要对每一个正例进行类分类，contrastive loss为：

其中，是一个critic，它把K维的局部/全局特征映射为一个常数。一般的，定义为：

其中，是critic network，把局部和全局特征投影到高维RKHS。实际上，是只有一个hidden layer的浅网络（shallow networks），但是有谱归一化权重（spectral normalized weights）（参考1，参考2）。这些浅网络只用于投影输入特征的特征纬度，且保留原始空间的大小（spatial sizes）。

为稳定训练，限制鉴别器和生成器只能从虚假图像特征的contrastive loss中学习，而不能从真实图像特征的contrastive loss中学习。生成器和鉴别器的loss表示为：

其中， 是超参数；分别表示修正（fixed）的鉴别器和生成器；分别表示真实图像和生成图像的集合；是GAN的loss：

实际上，为简化起见，对于所有的实验，设置。消融实验（ablation study）显示，InfoMax-GAN适用很多的值。 

3.3 缓解Catastrophic Forgetting

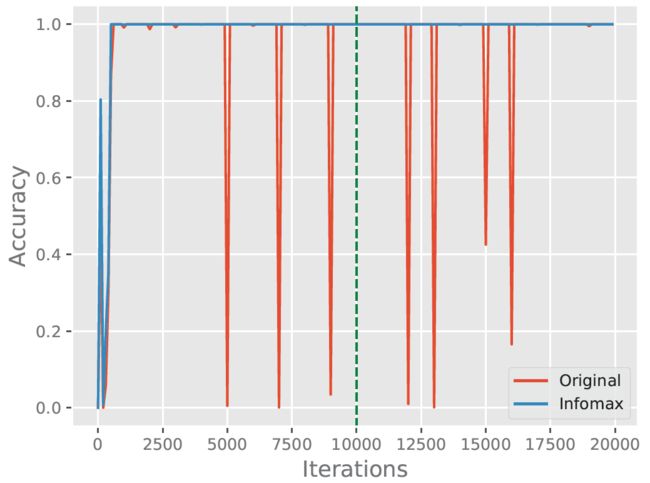
作者在one-vs-all CIFAR-10分类任务上训练了一个鉴别分类器：每1K次迭代改变类别分布，每10K次迭代是一个cycle。测试结果如上图所示：

• 没有InfoMax，分类器过拟合于某个特定的类别分布，所以当类别分布改变时，精度很低。
• 有Infomax，当类别分布改变时，鉴别分类器仍记得所有之前的类别。

3.4 缓解Mode Collapse

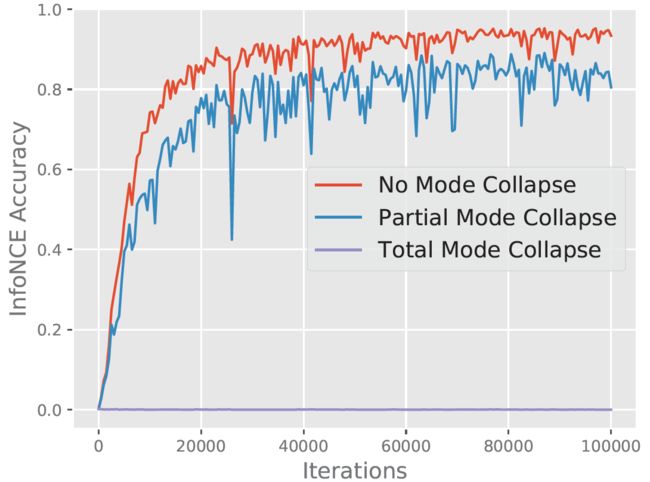
作者用CIFAR-10的training data训练了一个用于contrastive task的鉴别器，并用CIFAR-10的testing data模拟了三种生成器。

如上图所示，无mode collapse得完美生成器可以很好地处理contrastive task。

完全mode collapse的生成器只能生成一类图像，因此contrastive task的精度为0。对于任意N个图像，在contrastive task中共有个样本需要分类。对每个正例来说，有个负例。然而，如果由于完全地mode collapse使所有的N个图像都相同，那么存在个负例与每一个正例相同，这使得contrastive tas几乎不可能完成。因此，为完成contrastive task，生成器生成的图像要有更多的多样性，从而减少mode collapse。

如上图所所示，确实任意一个类别的图像（partial mode collapse）都会导致性能的下降。

4. Experiment

4.1 Experiment Settings

• Training：所有的model用相同的residual network backbone训练。
• Evaluation：使用三个不同的度量评估生成图像的质量。Fréchet Inception Distance（FID），Kernel Inception Distance（KID）和InceptionScore（IS）。一般而言，FID和KID用于评估生成图像的多样性（越小越好），IS用于评估生成图像的质量（越大越好）。对于所有的数值，进行三次实验，获得均值和标准差。

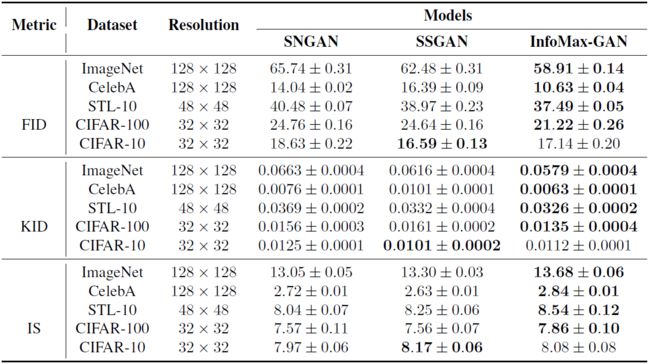
4.2 生成性能评估

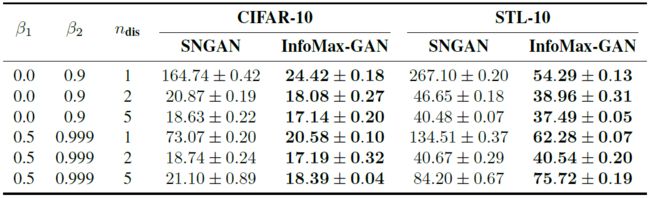
结果表明InfoMax-GAN具有优异的性能。在FID一栏中，InfoMax-GAN相比于SSGAN的增益，在CIFAR-100上要高于在CIFAR-10上。作者认为这是由于SSGAN倾向于生成易于旋转的图像（easily rotated images），这牺牲了多样性。更多的类别意味着更低的FID值。

4.3 Training Stability

本文测试了training stability，通过评估：当超参数在很大范围内变动时，model的性能变化。超参数包括Adam参数，生成器每update一次时鉴别器update的次数 ，等等。所有这些参数都是从以前性能优异的GAN作品中选取。

上图数据（FID）显示，即使GAN的训练未完成（例如，），InfoMax-GAN也有更好的性能。对于不同的参数，相比于SNGAN，InfoMax-GAN的FID稳定地维持在较低的水平，这说明了InfoMax-GAN的对超参数的robustness，不需要任何超参数调试就能获得良好的性能。这在实际中是有用的：当训练新的GAN或使用新的dataset时，若超参数未调好，则训练会十分的不稳定。而对超参数的robustness可以解决这个问题。

如图所示，红蓝分别表示随着迭代次数的增加，SNGAN和InfoMax-GAN的FID的变化。GAN训练更快地收敛并在整个过程中持续提升性能，可以稳定GAN训练。这归因于一个额外的约束：全局特征与其所有局部特征具有高互信息。从而约束生成的数据分布的空间，并导致生成数据变化较少，最终稳定GAN训练环境。当给定固定的计算预算来训练GAN时，这是一个实际的好处，因为在训练早期就可获得显著的性能提升。 

4.4 低计算量

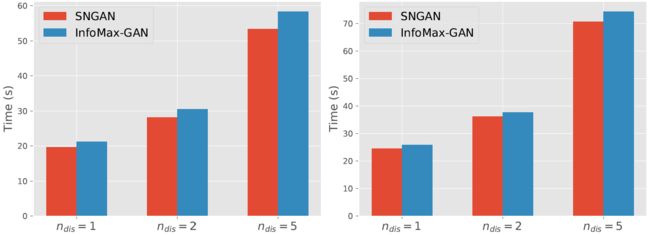
如图所示，InfoMax-GAN的训练所需时间很短。这是因为，在实际中，只有两个浅的（一个hidden layer）MPL网络需要计算contrastive loss。此外，所需的时间比时所需的时间少很多。这是因为大的是训练时间的一个重要瓶颈（bottleneck）。

上图数据是为了说明训练InfoMax-GAN的计算量低，所需时间短。但是刚看到这张图的时候我还以为是SNGAN和InfoMax-GAN的图注标错了。因为明显的InfoMax-GAN所需的时间要比SNGAN长。反复阅读了本节的相关描述，猜测这里InfoMax-GAN并不是要与SNGAN作对比。但如果不是和SNGAN作对比，这里又没有其他GAN训练的时间，描述里也没有作为参考的基准，这很难让人体会到InfoMax-GAN的低计算量。

然后我在其相关的参考文献中才找到答案。在“SPECTRAL NORMALIZATION FOR GENERATIVE ADVERSARIAL NETWORKS”一文中有如下描述the relative computational cost of the power iteration (18) is negligible when compared to the cost of forward and backward propagation on CIFAR-10。这是在说相比于在CIFAR-10上的FP和BP，SNGAN的计算量微不足道。因此，InfoMax-GAN和SNGAN进行对比才能显示出InfoMax-GAN的低计算量（但这单从图里是看不出来的）。

4.5 消融实验（Ablation Studies）

ablation study往往是在论文最终提出的模型上，减少一些改进特征（如减少几层网络等），以验证相应改进特征的必要性。
（一般在跑ablation study的时候发现去掉改进效果更好的情况也是常有的）

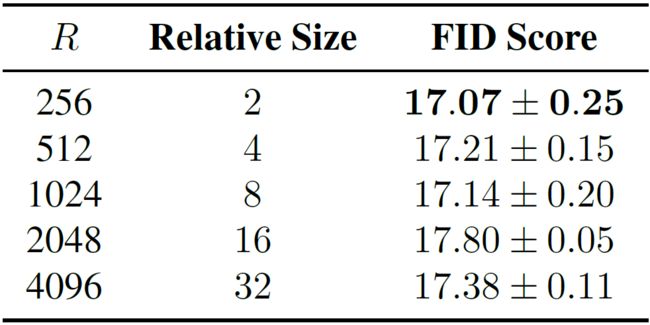
RKHS维度（R）：如上图所示，对于不同的R值，InfoMax-GAN的FID稳定地保持在较低水平，体现了robustness。这是因为InfoMax-GAN的critics是只有单个hidden layer的MLP networks，足够实现好的representation。

如上图所示，对于不同的超参数，

• InfoMax-GAN都有较低的FID值且在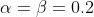时取得最好性能。
• 从图（b）可以看出，鉴别器对于提升GAN的性能是很重要的：保持，当的值从0.0增大到0.2时，FID逐渐减少。
• 当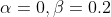时，InfoMax-GAN的目标函数仅添加鉴别器作为正则项就能获得良好的性能。这是因为互信息最大化可以减少catastrophic forgetting，从而稳定GAN的训练。
• 继续增大的值可以进一步提升性能。这是因为生成器的正则化项有助于减少mode collapse从而提升FID。

5. 补充：谱归一化（spectral normalization）

5.1 理论依据

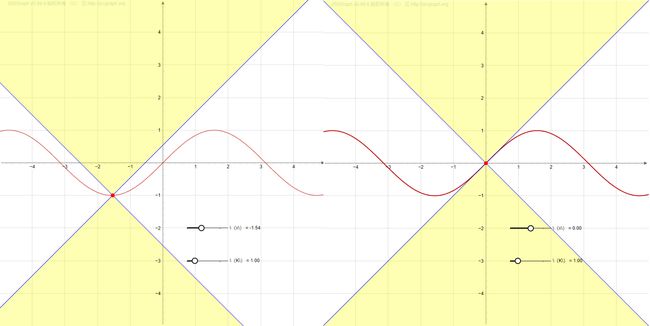
利普希茨连续性（Lipschitz continuity）是形容一个函数“好”的特性。以一维函数为例，如果该函数是利普希茨连续的，那我我们可以找到一个圆锥体，以函数图像上每个点为中心的圆锥体，都使函数图像位于该圆锥体之外。如下图所示，

如果一个一维函数是可微的，那么它的利普希茨常数（Lipschitz constant）K是其导数的最大值。利普希茨连续性要求K是有界量，这就限制了鉴别器的梯度，从而解决了gradient descent过程中梯度爆炸的问题。

一般可微函数的利普希茨常数是其最大奇异值（largest singular value）或谱范数（spectral norm）。

谱归一化的前提是：对于任意多层的鉴别器（可能是线性映射与非线性分量的复合函数），可以找到利普希茨常数或者其上界。

5.2 算法

随机初始化两个向量，令网络权重，其中，是W的最大奇异值，计算它的操作叫做power iteration，操作如下：

经过多次迭代，将收敛为W的特征向量。

该算法相比于梯度下降，计算量很小。

6. 参考

1. Lee K S, Tran N T, Cheung N M. Infomax-gan: Improved adversarial image generation via information maximization and contrastive learning[C]//Proceedings of the IEEE/CVF winter conference on applications of computer vision. 2021: 3942-3952. 下载地址：WACV 2021 Open Access Repository (thecvf.com)​​​​​​
2. Spectral Normalization for GAN - 知乎
3. Spectral Normalization Explained
4. Miyato T, Kataoka T, Koyama M, et al. Spectral normalization for generative adversarial networks[J]. arXiv preprint arXiv:1802.05957, 2018. 下载地址：[1802.05957] Spectral Normalization for Generative Adversarial Networks (arxiv.org)
5. 什么是ablation study（消融实验）？_诸神缄默不语的博客-CSDN博客_消融实验