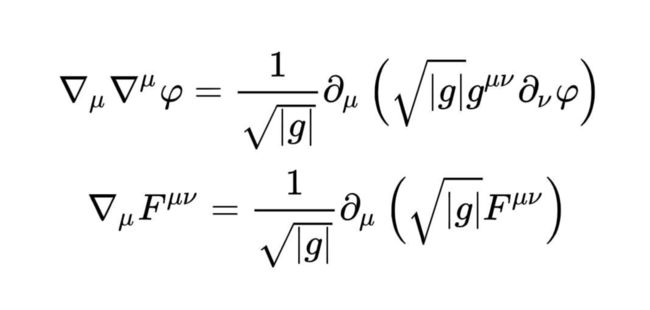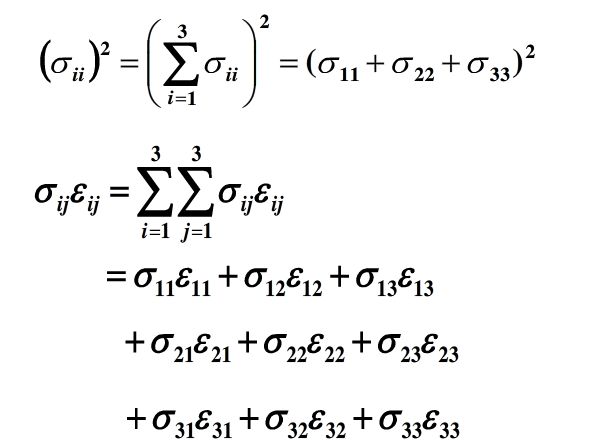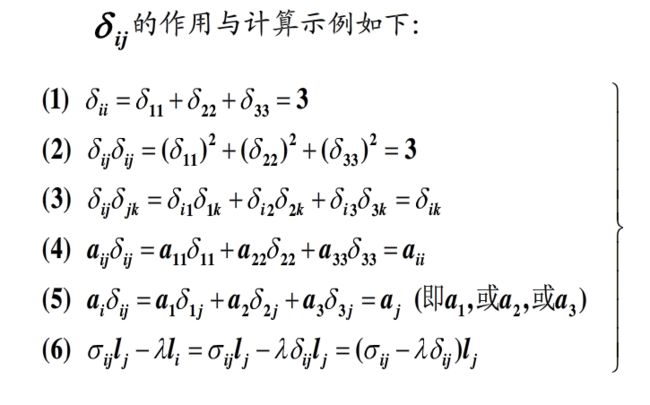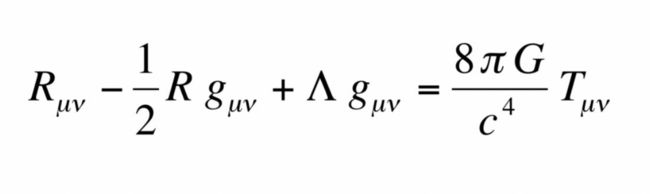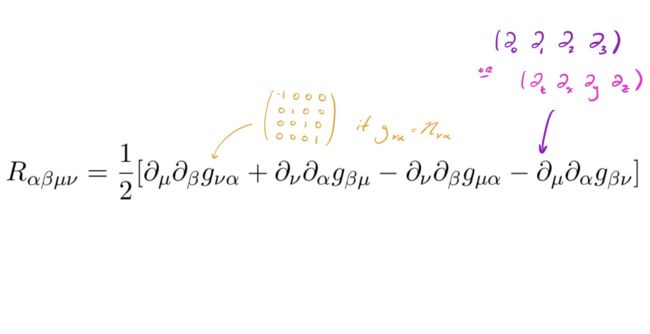张量(Tensor)
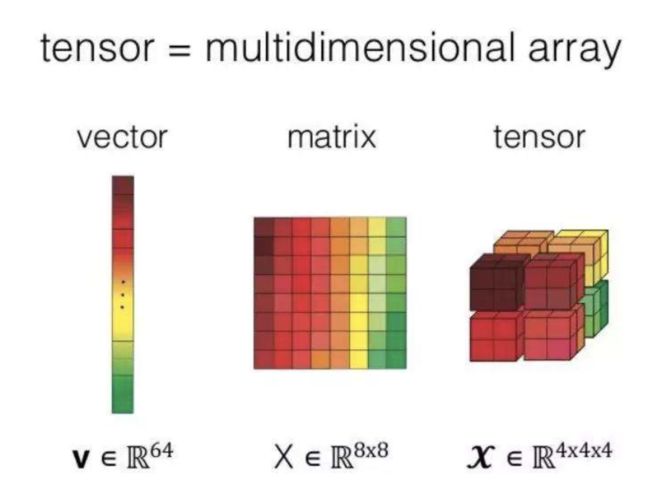
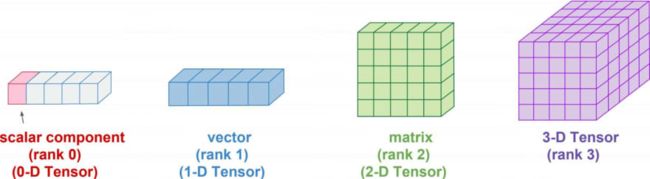
张量是矢量和矩阵概念的推广,标量是0阶张量,矢量是1阶张量,矩阵是二阶张量,而三阶张量好比是立方体矩阵。
张量是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数。
张量的出现是有原因的,因为我们无法用标量和向量完整的表示所有的物理量,所以物理学家使用的数学量的概念就必须扩大,所以张量就出现了。张量之所以重要,在于它可以满足一切物理定律必须与坐标系的选择无关的特性。
张量(Tensor)是一个定义在一些向量空间和一些对偶空间的笛卡儿积上的多重线性映射,其坐标是|n|维空间内,有|n|个分量的一种量, 其中每个分量都是坐标的函数, 而在坐标变换时,这些分量也依照某些规则作线性变换。r 称为该张量的秩或阶(与矩阵的秩和阶均无关系)。
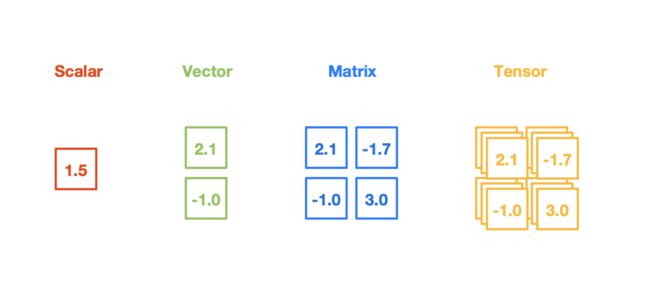
在同构的意义下,第零阶张量 (r = 0) 为标量 (Scalar),第一阶张量 (r = 1) 为向量 (Vector), 第二阶张量 (r = 2) 则成为矩阵 (Matrix)。例如,对于3维空间,r=1时的张量为此向量:(x,y,z)。由于变换方式的不同,张量分成协变张量 (Covariant Tensor,指标在下者)、逆变张量 (Contravariant Tensor,指标在上者)、 混合张量 (指标在上和指标在下两者都有) 三类。
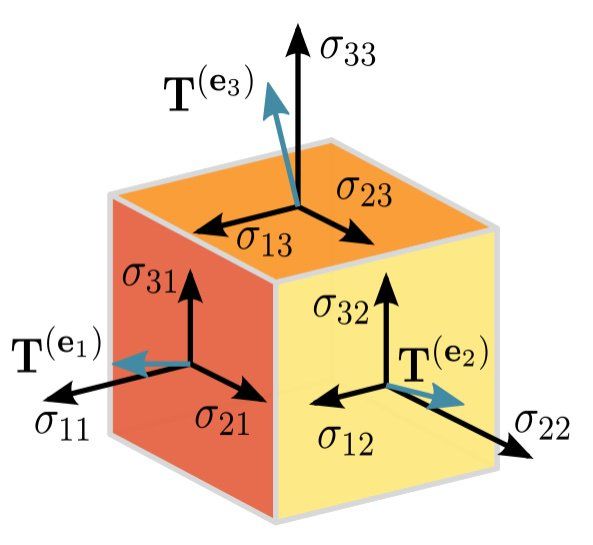
在数学里,张量是一种几何实体,或者说广义上的“数量”。张量概念包括标量、向量和线性算子。张量可以用坐标系统来表达,记作标量的数组,但它是定义为“不依赖于参照系的选择的”。张量在物理和工程学中很重要。例如在扩散张量成像中,表达器官对于水的在各个方向的微分透性的张量可以用来产生大脑的扫描图。可能最重要的工程上的例子就是应力张量和应变张量了,它们都是二阶张量,对于一般线性材料他们之间的关系由一个四阶弹性张量来决定。
虽然张量可以用分量的多维数组来表示,张量理论存在的意义在于进一步说明把一个数量称为张量的涵义,而不仅仅是说它需要一定数量的有指标索引的分量。特别是,在坐标转换时,张量的分量值遵守一定的变换法则。张量的抽象理论是线性代数分支,现在叫做多重线性代数。
“张量”一词最初由威廉·罗恩·哈密顿在1846年引入,但他把这个词用于指代现在称为模的对象。该词的现代意义是沃尔德马尔·福格特在1899年开始使用的。
这个概念由格雷戈里奥·里奇-库尔巴斯特罗在1890年在《绝对微分几何》的标题下发展出来,随着1900年列维-奇维塔的经典文章《绝对微分》(意大利文,随后出版了其他译本)的出版而为许多数学家所知。随着1915年左右爱因斯坦的广义相对论的引入,张量微积分获得了更广泛的承认。广义相对论完全由张量语言表述,爱因斯坦从列维-奇维塔本人那里学了很多张量语言(其实是Marcel Grossman,他是爱因斯坦在苏黎世联邦理工学院的同学,一个几何学家,也是爱因斯坦在张量语言方面的良师益友 - 参看Abraham Pais所著《上帝是微妙的(Subtle is the Lord)》),并学得很艰苦。但张量也用于其它领域,例如连续力学,譬如应变张量(参看线性弹性)。
注意“张量”一词经常用作张量场的简写,而张量场是对流形的每一点给定一个张量值。要更好的理解张量场,必须首先理解张量的基本思想。
形象直观地来理解张量
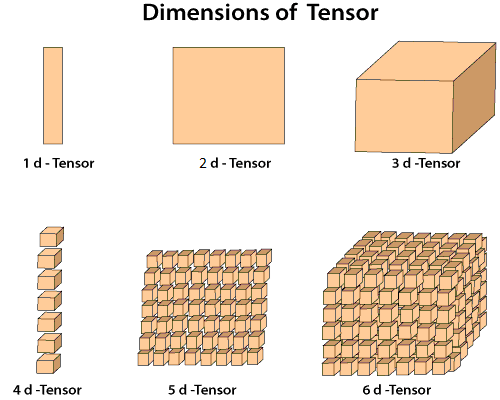
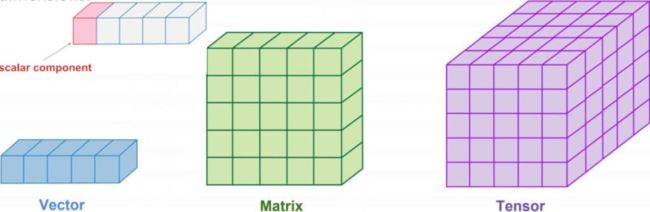
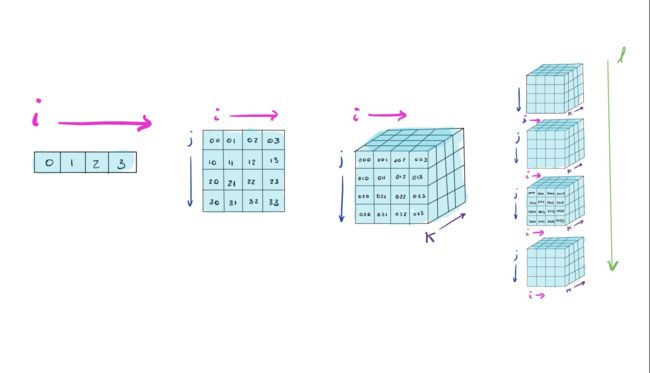
Below is the diagram that describes the Tensor's dimensions in a very efficient way.
Now let's get a little bit knowledge about the notation of Tensors
The tensor notation is similar to the metrics notation. A capital letter represents the tensor, and the lower letter with subscript integer represents scalar values within the tensor.
符号约定
下标标记法
求和约定
关于自由标号
同一方程式中,各张量的自由标号相同,即同阶标号字母相同。
关于Kronecker delta (δij)符号
张量的基本运算
https://www.cnblogs.com/arxive/p/4967486.html
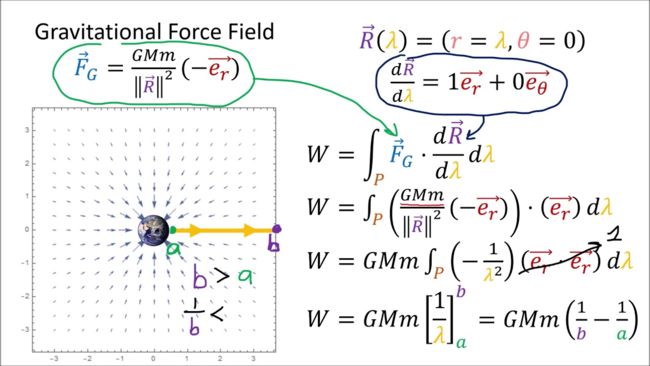
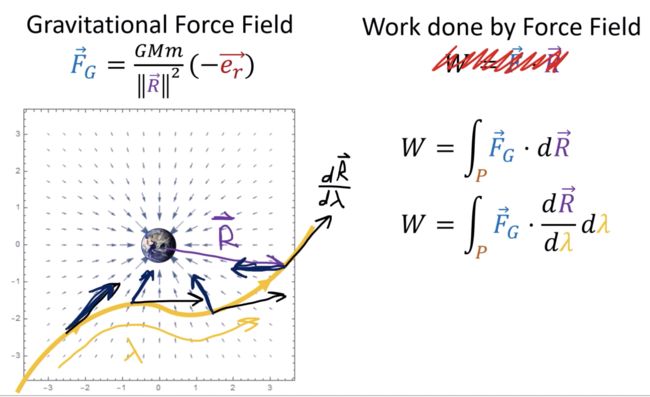
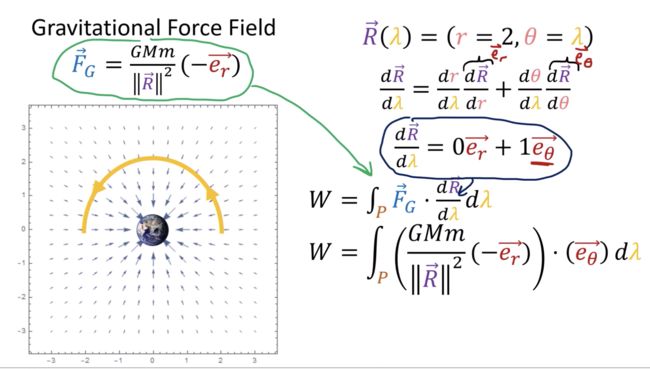
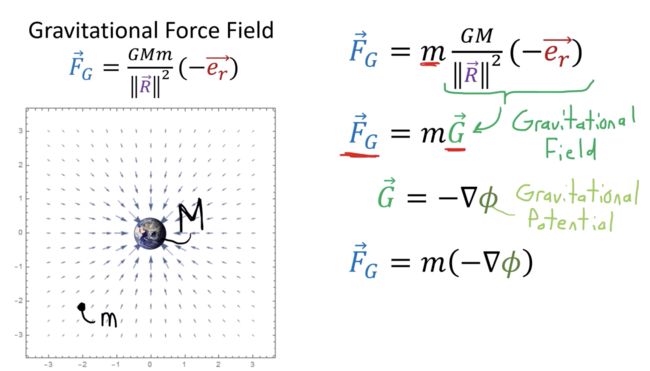
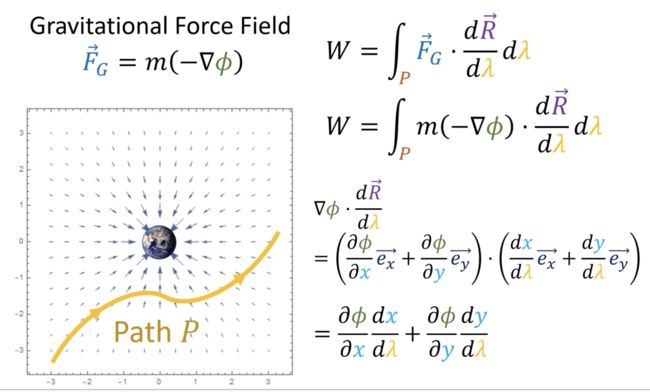
引力场
https://dev.to/juancarlospaco/tensors-for-busy-people-315k
How it looks like on Code?.
Scalar
letmyscalar=42
Scalar can be a variety of things, usually numeric values, to keep things simple and easy to understand we will use an integer here, 42 is our Scalar.
Vector
letmyvector=[1,2,3]
Vector is a collection of items, we continue using integers, it can be seen on the code as an array or list, you can draw it as a Rank 1 Vector.
Matrix
letmymatrix=[[1,2,3],[4,5,6],]
We continue adding dimensions then we end up with the Matrix, a 2D Tensor, can be simplified on code as a list with lists inside.
Tensor
letmytensor=[[[1,2,3],[4,5,6],],[[7,8,9],[10,11,12],],]
Wow, we reached the crazy cube, a multiple dimensions array of integers,
we need to convert this jam of lists into a Tensor object!.
Tensor Arraymancer
importarraymancerletmytensor=[[[1,2,3],[4,5,6],],[[7,8,9],[10,11,12],],].toTensor
Done, congrats you coded your first Tensor!.
Tensor can be categorized by rank, i.e. how many "rows and columns they have."
Rank 0: Scalar/Number
Rank 1: Vector
Rank 2: NxN matrix
Rank >= 3: Tensor
I did a visualization of these ranks below
Why are tensors important though?
Well, engineers use them a lot when dealing with the forces and stresses on an object.
Relativists use them to package equations like the Einstein Field Equations which would otherwise be (4x4)16 equations! Wow!
How many equations do you think the Riemann Curvature Tensor below can package?
In the field of Physics and Engineering, as a tool, tensor and tensor algebra widely used. We can say it is a set of techniques in machine learning in the operation and training of deep learning models can be described regarding tensors.
Dot product of two 4D tensors
https://discuss.pytorch.org/t/dot-product-of-two-4d-tensors/69555
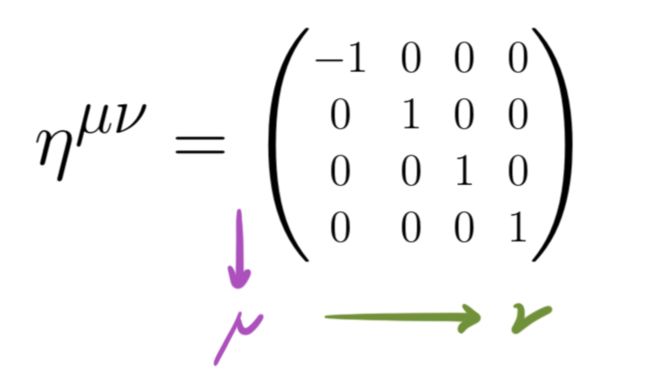
度量张量
参考资料
https://www.youtube.com/watch?v=f5liqUk0ZTw
https://www.youtube.com/watch?v=e0eJXttPRZI
https://www.zhihu.com/question/23720923