机器学习中的正则化——L1范数和L2范数
机器学习中的正则化——L1范数和L2范数
- 正则化是什么?为什么要正则化?
- LP范数
-
- L0范数(补充了解)
- L1范数
- L2范数
- L1范数和L2范数的区别
- 以深度学习的角度看待L1范数和L2范数
正则化是什么?为什么要正则化?
在数学与计算机科学中,尤其是在机器学习和逆问题领域中,正则化是指为解决适定性问题或过拟合而加入额外信息的过程。 在机器学习和逆问题的优化过程中,正则项往往被加在目标函数当中。——维基百科
正则化的本质是对某一问题加以先验的限制或约束(如L1范数和L2范数),以达到某种特定目的的一种手段或操作(函数的稀疏或者平滑)。在算法中使用正则化的目的是防止模型出现过拟合。
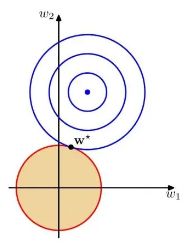
正则化的作用,以下图为例进行说明:
在机器学习的任务中,我们是在一个可行解空间(图中的黄色区域)中找到最优解或符合任务目标的解(某一个点)。在未加入正则化之前,这个可行解空间是无边界限制的。通过加入正则化后,这个可行解空间被限制在一个特定的范围内。不同的正则化方法,对可行解产生的限制也不同。

在进一步了解L1范数和L2范数之前,我们需要先了解LP范数是什么。
LP范数
范数是一种强化了的距离概念,它在定义上比距离多了一条数乘的运算法则。有时候为了便于理解,我们可以把范数简单可以理解为用来表征向量空间中的距离,而距离的定义很抽象,只要满足非负(距离不能为负)、自反(A点到B点的距离量度与反之,相等)、三角不等式(三角形不等式)就可以称之为距离。
与闵可夫斯基距离的定义一样,L-P范数不是一个范数,而是一组范数,其定义如下:
∥ x ∥ p = ( ∑ i n x i p ) 1 p \|x\|_{p}=\left(\sum_{i}^{n} x_{i}^{p}\right)^{\frac{1}{p}} ∥x∥p=(i∑nxip)p1
根据P 的变化,范数也有着不同的变化,一个经典的有关P范数的变化图如下:


三维空间中到原点的距离(范数)为1的点构成的图形的变化情况。以常见的L-2范数(p=2)为例,此时的范数也即欧氏距离,空间中到原点的欧氏距离为1的点构成了一个球面。
上图表示了p从0到正无穷变化时,单位球(unit ball)的变化情况。在P范数下定义的单位球都是凸集,但是当0 当P=0时,也就是L0范数,由上面可知,L0范数并不是一个真正的范数,它主要被用来度量向量中非零元素的个数。用上面的L-P定义可以得到的L-0的定义为: ∥ x ∥ 0 = ∑ i = 1 n x i 0 0 \|\mathbf{x}\|_{0}=\sqrt[0]{\sum_{i=1}^{n} x_{i}^{0}} ∥x∥0=0i=1∑nxi0 但是零的零次方,非零数开零次方都是什么鬼,很不好说明L0的意义,所以在通常情况下,大家都用的是: ∥ x ∥ 0 = # ( i ∣ x i ≠ 0 ) \|\mathrm{x}\|_{0}=\#\left(i \mid x_{i} \neq 0\right) ∥x∥0=#(i∣xi=0) 表示向量x中非零元素的个数。 我们可以通过最小化L0范数,来寻找最少最优的稀疏特征项。对于L0范数,其优化问题为: min ∥ x ∥ 0 , s . t . A x = b \min \|\mathrm{x}\|_{0},s.t. A x=b min∥x∥0,s.t.Ax=b 但不幸的是,L0范数的最优化问题是一个NP hard问题(L0范数同样是非凸的)。因此,在实际应用中我们经常对L0进行凸松弛,理论上有证明,L1范数是L0范数的最优凸近似,所以在实际情况中,L0的最优问题会被放宽到L1或L2下的最优化。 L1范数的数学形式: ∥ x ∥ 1 = ∑ i n ∣ x i \|x\|_{1}=\sum_{i}^{n} \mid x_{i} ∥x∥1=i∑n∣xi 表示向量x中非零元素的绝对值之和。 L1范数有很多的名字,例如我们熟悉的曼哈顿距离、最小绝对误差等。使用L1范数可以度量两个向量间的差异,如绝对误差和(Sum of Absolute Difference): S A D ( x 1 , x 2 ) = ∑ i n ∣ x 1 i − x 2 i ∣ S A D\left(x_{1}, x_{2}\right)=\sum_{i}^{n}\left|x_{1 i}-x_{2 i}\right| SAD(x1,x2)=i∑n∣x1i−x2i∣ 对于L1范数,它的优化问题如下: min ∥ x ∥ 1 , s . t . A x = b \min \|\mathbf{x}\|_{1},s.t. A x=b min∥x∥1,s.t.Ax=b 由于L1范数就是向量各元素的绝对值之和,对L1优化的解是一个稀疏解,因此L1范数也被叫做稀疏规则算子。为什么我们希望稀疏化?稀疏化有很多好处,最直接的两个: 通过L1可以实现特征的稀疏,去掉一些没有信息的特征。例如在对用户的电影爱好做分类的时候,用户有100个特征,可能只有十几个特征是对分类有用的,大部分特征如身高体重等可能都是无用的,利用L1范数就可以过滤掉。 L2范数的数学形式: ∥ x ∥ 2 = ∑ i n ( x i ) 2 \|x\|_{2}=\sqrt{\sum_{i}^{n}\left(x_{i}\right)^{2}} ∥x∥2=i∑n(xi)2 表示向量元素的平方和再开平方。L2范数有很多名称,有人把它的回归叫“岭回归”(Ridge Regression),也有人叫它“权值衰减”(Weight Decay)。 L2也可以度量两个向量间的差异,如平方差和(Sum of Squared Difference): SSD ( x 1 , x 2 ) = ∑ i = 1 n ( x 1 i − x 2 i ) 2 \operatorname{SSD}\left(x_{1}, x_{2}\right)=\sum_{i=1}^{n}\left(x_{1 i}-x_{2 i}\right)^{2} SSD(x1,x2)=i=1∑n(x1i−x2i)2 对于L2范数,它的优化问题如下: min ∥ x ∥ 2 , s . t . A x = b \min \|\mathbf{x}\|_{2},s.t. A x=b min∥x∥2,s.t.Ax=b 以L2范数作为正则项可以得到稠密解,即每个特征对应的参数w都很小,接近于0但是不为0;此外,L2范数作为正则化项,可以防止模型为了迎合训练集而过于复杂造成过拟合的情况,从而提高模型的泛化能力。 以PRML一个经典的图来说明下L1和L2范数的区别,如下图所示: 从贝叶斯先验的角度看,当训练一个模型时,仅依靠当前的训练数据集是不够的,为了实现更好的泛化能力,往往需要加入先验项,而加入正则项相当于加入了一种先验。 我们先来看深度学习中的loss计算 loss = min w 1 2 n ∥ w X − y ∥ 2 2 \operatorname{loss}=\min _{w} \frac{1}{2 n}\|w X-y\|_{2}^{2} loss=wmin2n1∥wX−y∥22 加L1范数,即在loss计算的尾部加上 β ∥ w ∥ 1 \beta\|w\|_{1} β∥w∥1,L2范数,同上。 对于神经网络的反向传播,是将loss对w的求导值,通过学习率的调节施加在W的更新上,如下: W + = W − α ∂ loss ∂ w W^{+}=W-\alpha \frac{\partial \operatorname{loss}}{\partial \mathrm{w}} W+=W−α∂w∂loss 对于分别加入L1范数和L2范数的求导,则如下。 L1范数: W + = W − α ∂ ( min w 1 2 n ∥ w X − y ∥ 2 2 + β ∥ w ∥ 1 ) ∂ w W^{+}=W-\alpha \frac{\partial\left(\min _{w} \frac{1}{2 n}\|w X-y\|_{2}^{2}+\beta\|w\|_{1}\right)}{\partial w} W+=W−α∂w∂(minw2n1∥wX−y∥22+β∥w∥1) W + = W − [ α ∂ ( min W 1 2 n ∥ w X − y ∥ 2 2 ) ∂ w + β ] W^{+}=W-\left[\alpha \frac{\partial\left(\min _{W} \frac{1}{2 n}\|w X-y\|_{2}^{2}\right)}{\partial w}+\beta\right] W+=W−[α∂w∂(minW2n1∥wX−y∥22)+β] L2范数: W + = W − α ∂ ( min w 1 2 n ∥ w X − y ∥ 2 2 + β ∥ w ∥ 2 ) ∂ w W^{+}=W-\alpha \frac{\partial\left(\min _{w} \frac{1}{2 n}\|w X-y\|_{2}^{2}+\beta\|w\|_{2}\right)}{\partial w} W+=W−α∂w∂(minw2n1∥wX−y∥22+β∥w∥2) W + = W − [ α ∂ ( min W 1 2 n ∥ w X − y ∥ 2 2 ) ∂ w + β w ] W^{+}=W-\left[\alpha \frac{\partial\left(\min _{W} \frac{1}{2 n}\|w X-y\|_{2}^{2}\right)}{\partial w}+\beta w\right] W+=W−[α∂w∂(minW2n1∥wX−y∥22)+βw]L0范数(补充了解)
L1范数
L2范数
L1范数和L2范数的区别

如上图所示,蓝色的圆圈表示问题可能的解范围,橘色的表示正则项可能的解范围。而整个目标函数(原问题+正则项)有解当且仅当两个解范围相切。从上图可以很容易地看出,由于L2范数解范围是圆,所以相切的点有很大可能不在坐标轴上,而由于L1范数是菱形(顶点是凸出来的),其相切的点更可能在坐标轴上,而坐标轴上的点有一个特点,其只有一个坐标分量不为零,其他坐标分量为零,即是稀疏的。所以有如下结论,L1范数可以导致稀疏解,L2范数导致稠密解。
以深度学习的角度看待L1范数和L2范数
因此,以L2范数作为正则项可以得到稠密解,即每个特征对应的参数w都很小,接近于0但是不为0;此外,L2范数作为正则化项,可以防止模型为了迎合训练集而过于复杂造成过拟合的情况,从而提高模型的泛化能力。

