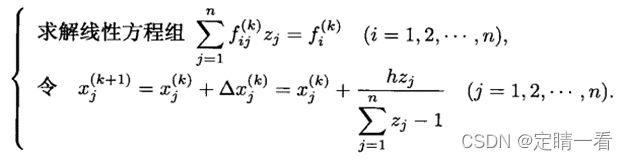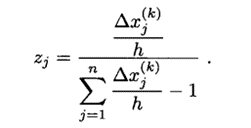迭代法求解非线性方程组（含python代码）

1. 迭代法求解非线性方程组的原理

        参考西安交大数值分析教材

 

 

 

 

 

 

 

 

 

 

2. 迭代法求解非线性方程组的计算过程

        牛顿法求解非线性方程组的计算过程如下

         弦割法与牛顿法类似，弦割法将牛顿法中的偏导数用差商替代，即将上述牛顿法中的第(ii)步和第(iii)步转化为以下迭代格式

 

         布罗伊登法求解非线性方程组的计算过程如下

 3. 程序使用说明

        程序使用方法为：（1）定义自变量；（2）使用（1）中的自变量定义非线性方程组列表；（3）给定初值，精度以及迭代次数；（4）调用方程netwon()，broyden()，string_cut()，分别对应牛顿法，布罗伊登法和弦割法。具体如下所示

4. python实现代码

 

'''
使用牛顿法、弦割法、布罗伊登法求解非线性方程组
'''
import sympy
import pprint
import numpy as np

#计算向量范数
def Norm2(p):
    sum_of_p = sum([i ** 2 for i in p])
    return sum_of_p ** 0.5

#牛顿法
def newton(A, x_0, args, prec=0.00000001, n=10):
    funcs=sympy.Matrix(A)
    args=args
    jacobianMatrix=funcs.jacobian(args) #计算雅可比矩阵
    #pprint.pprint(jacobianMatrix.inv())

    x_0=sympy.Matrix(x_0)
    x = args

    x_pre = x_0
    for k in range(0, n): #迭代求解
        b = - funcs.subs(zip(x, x_pre)) #计算f（x【k】）
        J = jacobianMatrix.subs(zip(x, x_pre))  #计算雅可比矩阵Jf（x【k】）
        deltx = sympy.Matrix(J.inv() * b) #使用雅可比矩阵的逆求解deltx
        x_new = x_pre + deltx  #迭代跟新x
        if Norm2(funcs.subs(zip(x, x_new))) < prec: #如果满足精度要求则返回
            #pprint.pprint(x_new)
            #print(k)
            return([x_new,k])
        x_pre = x_new
    return("迭代次数较少，无法满足精度要求")

#弦割法
def string_cut(A, x_0, args, prec=0.00000001, n=10):
    funcs = sympy.Matrix(A)
    #args = args
    h = 0.1 #设置h的大小
    e = np.eye(len(A))*h
    #pprint.pprint(e)
    x_0 = sympy.Matrix(x_0)
    x = args

    x_pre = x_0
    c=[]
    for k in range(0,n):
        for p in range(len(A)):
            c.append([A[p].subs(zip(x, (x_pre + sympy.Matrix(e[j]))))
                      for j in range(0, len(A))])
        fij = sympy.Matrix(c) #计算fij【k】
        #pprint.pprint(fij)
        b = funcs.subs(zip(x, x_pre)) #计算fi【k】
        z = fij.inv() * b  #求解z
        deltx = h * z / (sum(z) - 1)  #计算deltx
        x_new = x_pre + deltx #更新x
        if Norm2(funcs.subs(zip(x, x_new))) < prec: #满足精度要求则返回
            #pprint.pprint(x_new)
            #print(k)
            return([x_new,k])
        x_pre = x_new
        c = []
    return("迭代次数较少，无法满足精度要求")

def broyden(A, x_0, args, prec=0.00000001, n=10):
    funcs = sympy.Matrix(A)
    args = args
    jacobianMatrix = funcs.jacobian(args)

    x_0 = sympy.Matrix(x_0)
    x = args

    b = funcs.subs(zip(x, x_0))
    J0 = jacobianMatrix.subs(zip(x, x_0))
    x_1 = x_0 - J0.inv() * b
    prec = prec
    #以下得到两个初始迭代值和初始A【0】矩阵
    x_pre = x_0
    x_now = x_1
    J = jacobianMatrix.subs(zip(x, x_pre)).inv() #A【0】的逆
    #迭代计算
    for k in range(0, n):
        s = x_now - x_pre #计算s【k】
        y = funcs.subs(zip(x, x_now)) - funcs.subs(zip(x, x_pre)) #计算y【k】

        temp1 = (s - J * y) * s.T * J
        temp2 = (s.T * J * y)
        num = temp2 ** (-1)
        e=np.eye(len(A))
        n_num=np.array(num)
        e_num=e*(n_num)
        diag = sympy.diag(e_num)
        temp = temp1 * diag  #将除以一个数变为乘其逆的对角单位矩阵
        J_new = J + temp #得到A【k】的逆
        x_new = x_now - J_new * funcs.subs(zip(x, x_now)) #更新x的值
        if Norm2(funcs.subs(zip(x, x_new))) < prec: #如果满足精度要求则返回
            #pprint.pprint(x_new)
            #print(k)
            return [x_new, k]
        x_pre = x_now
        x_now = x_new
        J = J_new
    return ("迭代次数较少，无法满足精度要求")


if __name__ == "__main__":
    #---------------------------计算实习7.3.1-------------------------------
    x1, x2, x3 = sympy.symbols("x1 x2 x3") #定义自变量
    args = sympy.Matrix([x1, x2, x3]) #定义自变量参数矩阵
    #定义非线性方程组列表
    A = [x1 ** 2 + x2 ** 2 + x3 ** 2 - 1.0,
         2 * x1 ** 2 + x2 ** 2 - 4 * x3 ** 2,
         3 * x1 ** 2 - 4 * x2 ** 2 + x3 ** 2]
    x_0 = [1.0, 1.0, 1.0] #设置初始向量
    prec = 0.00000001 #设置精度
    n=20 #设置迭代次数
    p = newton(A, x_0, args, prec, n) #牛顿法求解
    pprint.pprint(p)
    p = broyden(A, x_0, args, prec, n) #布罗伊登法求解
    pprint.pprint(p)
    p = string_cut(A, x_0, args, prec, n) #弦割法求解
    pprint.pprint(p)
    #----------------------------计算实习7.3.2-------------------------------
    # x1, x2 = sympy.symbols("x1 x2")
    # args = sympy.Matrix([x1, x2])
    # A=[sympy.cos(x1**2+0.4*x2)+x1**2+x2**2-1.6, 1.5*x1**2-1/0.36*x2**2-1.0]
    # x_0=[1.04, 0.47]
    # prec = 0.00000001
    # n=20
    # p = newton(A, x_0, args, prec, n)
    # pprint.pprint(p)
    # p = broyden(A, x_0, args, prec, n)
    # pprint.pprint(p)
    # p = string_cut(A, x_0, args, prec, n)
    # pprint.pprint(p)