深度学习系列四——优化篇之网络正则化
网络正则化
- 1、概述
- 2、 L 1 L_1 L1和 L 2 L_2 L2正则化
- 3、权重衰减
- 4、提前停止
- 5、丢弃法(Dropout)
-
- 5.1 循环神经网络上的丢弃法
- 6、数据增强
- 7、标签平滑
1、概述
\quad \quad 1、神经网络的泛化能力是影响模型能力的最关键因素,如何提高泛化能力是建立模型考虑的问题之一。
\quad \quad 2、神经网络可能存在过拟合问题–高方差,影响模型的泛化能力。因此,在建立模型时应避免过拟合。解决过拟合有两种方法:
- 正则化
- 训练集数据增强
\quad \quad 3、正则化(Regularization)是一类通过限制模型复杂度,从而避免过拟合,提高泛化能力的方法,比如引入约束、增加先验、提前停止等。
\quad \quad 4、在传统的机器学习中,提高泛化能力的方法主要是限制模型复杂度,比如采用 L 1 L_1 L1 和 L 2 L_2 L2正则化等方式。而在训练深度神经网络时,特别是在过度参数化(Over-Parameterization)时, L 1 L_1 L1 和 L 2 L_2 L2 正则化的效果往往不如浅层机器学习模型中显著。
\quad \quad 5、过度参数化是指模型参数的数量远远大于训练数据的数量。
\quad \quad 6、因此训练深度学习模型时,往往还会使用其他的正则化方法,比如数据增强、提前停止、丢弃法、集成法等。
2、 L 1 L_1 L1和 L 2 L_2 L2正则化
\quad \quad L 1 L_1 L1和 L 2 L_2 L2是机器学习中最常用的正则化方法,通过约束参数的 L 1 L_1 L1和 L 2 L_2 L2范数来减小模型在训练数据集上的过拟合现象。
3、权重衰减
\quad \quad 权重衰减(Weight Decay)是一种有效的正则化方法[Hanson et al., 1989],在每次参数更新时,引入一个衰减系数.
θ t = ( 1 − β ) θ t − 1 − α g t \theta_t=(1-\beta)\theta_{t-1}-\alpha g_t θt=(1−β)θt−1−αgt
其中 g t g_t gt为第 步更新时的梯度, 为学习率, 为权重衰减系数,一般取值比较小,比如 0.0005。在标准的随机梯度下降中,权重衰减正则化和 L 2 L2 L2正则化的效果相同。因此,权重衰减在一些深度学习框架中通过 L 2 L_2 L2 正则化来实现.但是,在 较为复杂的优化方法(比如 Adam)中,权重衰减正则化和 L 2 L_2 L2正则化并不等价
4、提前停止
\quad \quad 提前停止(Early Stop)对于深度神经网络来说是一种简单有效的正则化方法。由于深度神经网络的拟合能力非常强,因此比较容易在训练集上过拟合。使用梯度下降法进行优化时,我们可以使用一个和训练集独立的样本集合,称为验证集(Validation Set),并用验证集上的错误来代替期望错误。当验证集上的错误率不再下降,就停止迭代。然而在实际操作中,验证集上的错误率变化曲线并不一定是平衡曲线,很可能是先升高再降低。因此,提前停止的具体停止标准需要根据实际任务进行优化。
5、丢弃法(Dropout)
\quad \quad 丢弃法(Dropout Method)是当训练一个深度神经网络时,我们可以随机丢弃一部分神经元(同时丢弃其对应的连接边)得到一个节点更少,规模更小的网络,来避免过拟合。

如上图所示,就是对隐藏层使用丢弃法产生的一种可能的结果。其中 h 2 h_2 h2和 h 5 h_5 h5被清零。这时输出值的计算不再依赖 h 2 h_2 h2和 h 5 h_5 h5,在反向传播时,与这两个隐藏单元相关的权重的梯度均为0。由于在训练中隐藏层神经元的丢弃是随机的,即 h 1 , … , h 5 h_1, \ldots, h_5 h1,…,h5都有可能被清零,输出层的计算无法过度依赖 h 1 , … , h 5 h_1, \ldots, h_5 h1,…,h5中的任一个,从而在训练模型时起到正则化的作用,并可以用来应对过拟合。在测试模型时,我们为了得到更加确定性的结果,一般不使用丢弃法。
\quad \quad 如何实施Dropout?
\quad \quad 方法有好几种,目前最常用的方法是倒置丢弃法(inverted dropout)。下面讲一下具体步骤。
具体步骤:
1、设置超参数保留率p(保留率p可以通过验证集选取)。
【一般来讲,对于隐藏层的神经元,其保留率p=0.5时效果最好,这对大部分的网络和任务都比较有效。当p=0.5时,在训练时有一半的神经元被丢弃,只剩余一半的神经元是可以激活的,随机生成的网络结构最具多样性。对于输入层的神经元,其保留率通常设为更接近1的数,使得输入变化不会太大,对输入层神经元进行丢弃时,相当于给数据增加噪声,以此来提高网络的鲁棒性。】
2、遍历神经网络的每一层每一个神经单元,以概率p判定是否保留,产生丢弃掩码
- 对于一个神经层 y = f ( W x + b ) y=f(Wx+b) y=f(Wx+b),引入一个
掩蔽函数mask(.)使得 y = f ( W m a s k ( x ) + b ) y=f(Wmask(x)+b) y=f(Wmask(x)+b)
掩蔽函数mask(.)定义:
m a s k ( x ) = { m ⊙ x 当 训 练 阶 段 时 p x 当 测 试 阶 段 时 mask(x)=\left\{ \begin{aligned} &m\odot x \quad 当训练阶段时\\ & px \quad \quad \quad当测试阶段时 \end{aligned} \right. mask(x)={m⊙x当训练阶段时px当测试阶段时
其中, m ∈ { 0 , 1 } D m\in \{ 0,1\}^D m∈{0,1}D是丢弃掩码,通过以概率p的伯努利分布随机生成。 - 在训练时,激活神经元的平均数量为原来的p倍。而在测试时,所有的神经元都是可以激活的,这会造成训练和测试时网络的输出不一致。为了缓解这个问题,在测试时需要将神经元的输入x乘以p,也就相当于把不同的神经网络做了平均。
3、最后将保留的量除以保留率p进行拉伸。
-
为什么进行拉伸?
具体来说,设随机变量 ξ i \xi_i ξi为1和0的概率分别为 p p p和 1 − p 1-p 1−p(即保留率与丢弃率)。对于隐藏层 h i h_i hi,使用上述丢弃法时我们计算新的隐藏单元 h i ′ h_i' hi′
h i ′ = ξ i p h i . h_i' = \frac{\xi_i}{p} h_i. hi′=pξihi.
\quad 由于 E ( ξ i ) = p E(\xi_i) = p E(ξi)=p,因此
E ( h i ′ ) = E ( ξ i ) p h i = h i . E(h_i') = \frac{E(\xi_i)}{p}h_i = h_i. E(hi′)=pE(ξi)hi=hi.
\quad 即丢弃法不改变其输入的期望值,也就是说对保留的神经元进行拉伸以后可以更好的保留输入的信息。
【代码之python】
import torch
def dropout(X, keep_prob):#数据,保留率p
X = X.float()
# 首先检查keep_prob值是否处于正确范围
assert 0 <= keep_prob <= 1
# 这种情况下把全部元素都丢弃,则全部置0
if keep_prob == 0:
return torch.zeros_like(X)
# 借助随机分布生成X的掩码,mask是一个布尔型数组,值为true和false
#布尔型数在python中,进行乘法运算,会将其翻译成1和0
mask = (torch.rand(X.shape) < keep_prob).float()
return mask * X / keep_prob#将保留的量进行拉伸
例子:
对丢弃法的理解
1、集成学习角度的解释
\quad \quad 每做一次丢弃,相当于从原始的网络中采样得到一个子网络。如果一个神经网络有 个神经元,那么总共可以采样出 2 n 2^n 2n 个子网络。每次迭代都相当于训练一个不同的子网络,这些子网络都共享原始网络的参数。那么,最终的网络可以近似看作集成了指数级个不同网络的组合模型。
2、贝叶斯学习角度的解释
\quad \quad 丢弃法也可以解释为一种贝叶斯学习的近似。用 = (; )来表示要学习的神经网络,贝叶斯学习是假设参数 为随
机向量,并且先验分布为(),贝叶斯方法的预测为
E q ( θ ) [ y ] = ∫ p f ( x ; θ ) q ( θ ) d θ ≈ 1 M ∑ m = 1 m f ( x , θ m ) E_{q(\theta)}[y]=\int_pf(x;\theta)q(\theta)d\theta\\ \approx\frac1M\sum_{m=1}^mf(x,\theta_m) Eq(θ)[y]=∫pf(x;θ)q(θ)dθ≈M1m=1∑mf(x,θm)
其中 f ( x , θ m ) f(x,\theta_m) f(x,θm)为第次应用丢弃方法后的网络,其参数 为对全部参数 的一次采样。
5.1 循环神经网络上的丢弃法
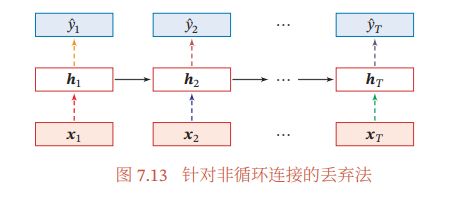
\quad \quad 当在循环神经网络上应用丢弃法时,不能直接对每个时刻的隐状态进行随机丢弃,这样会损害循环网络在时间维度上的记忆能力。一种简单的方法是对非时间维度的连接(即非循环连接)进行随机丢失 .如图7.13所示,虚线边表示进行随机丢弃,不同的颜色表示不同的丢弃掩码。
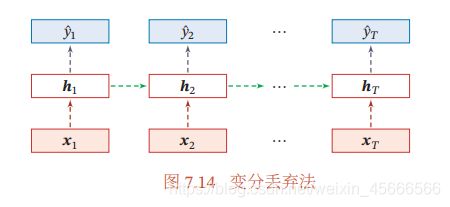
\quad \quad 然而根据贝叶斯学习的解释,丢弃法是一种对参数 的采样。每次采样的参数需要在每个时刻保持不变。因此,在对循环神经网络上使用丢弃法时,需要对参数矩阵的每个元素进行随机丢弃,并在所有时刻都使用相同的丢弃掩码。这种方法称为变分丢弃法(Variational Dropout)。图7.14给出了变分丢弃法的示例,相同颜色表示使用相同的丢弃掩码。
6、数据增强
\quad \quad 深度神经网络一般都需要大量的训练数据才能获得比较理想的效果.在数据量有限的情况下,可以通过数据增强(DataAugmentation)来增加数据量,提高模型鲁棒性,避免过拟合。 目前,数据增强还主要应用在图像数据上,在文本等
其他类型的数据上还没有太好的方法.
\quad \quad 图像数据的增强主要是通过算法对图像进行转变,引入噪声等方法来增加数据的多样性.增强的方法主要有几种:
(1) 旋转(Rotation):将图像按顺时针或逆时针方向随机旋转一定角度。
(2) 翻转(Flip):将图像沿水平或垂直方法随机翻转一定角度。
(3) 缩放(Zoom In/Out):将图像放大或缩小一定比例。
(4) 平移(Shift):将图像沿水平或垂直方法平移一定步长。
(5) 加噪声(Noise):加入随机噪声。
7、标签平滑
\quad \quad 标签平滑(Label Smoothing),即在输出标签中添加噪声来避免模型过拟合。
\quad \quad 一个样本的标签可以用one-hot向量表示,即
y = [ 0 , 0 , . . , 0 , 1 , 0 , . . , 0 ] T y=[0,0,..,0,1,0,..,0]^ T y=[0,0,..,0,1,0,..,0]T
这种标签可以看作硬目标(Hard Target)。如果使用Softmax分类器并使用交叉熵损失函数,最小化损失函数会使得正确类和其他类的权重差异变得很大。根据Softmax 函数的性质可知,如果要使得某一类的输出概率接近于 1,其未归一化的得分需要远大于其他类的得分,可能会导致其权重越来越大,并导致过拟合。此外,如果样本标签是错误的,会导致更严重的过拟合现象.为了改善这种情况,我们可以引入一个噪声对标签进行平滑,即假设样本以 ϵ \epsilon ϵ的概率为其他类。平滑后的标签为
y ^ = [ ϵ K − 1 , ϵ K − 1 , . . . , ϵ K − 1 , 1 − ϵ , ϵ K − 1 , . . , ϵ K − 1 ] T \hat{y}=[\frac{\epsilon}{K-1},\frac{\epsilon}{K-1},...,\frac{\epsilon}{K-1},1-\epsilon,\frac{\epsilon}{K-1},..,\frac{\epsilon}{K-1}]^T y^=[K−1ϵ,K−1ϵ,...,K−1ϵ,1−ϵ,K−1ϵ,..,K−1ϵ]T
其中 为标签数量,这种标签可以看作软目标(Soft Target).标签平滑可以避免模型的输出过拟合到硬目标上,并且通常不会损害其分类能力。
\quad \quad 上面的标签平滑方法是给其他 − 1个标签相同的概率 ϵ K − 1 \frac{\epsilon}{K-1} K−1ϵ,没有考虑标签之间的相关性。一种更好的做法是按照类别相关性来赋予其他标签不同的概率。比如先训练另外一个更复杂(一般为多个网络的集成)的教师网络(Teacher
Network),并使用大网络的输出作为软目标来训练学生网络(Student Network)。这种方法也称为知识蒸馏(Knowledge Distillation)。
参考资料:神经网络与深度学习