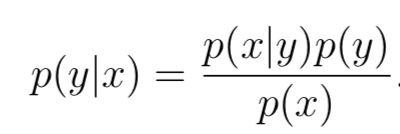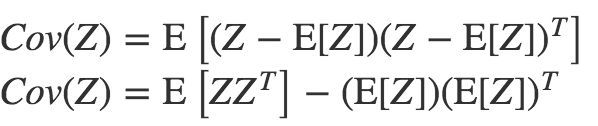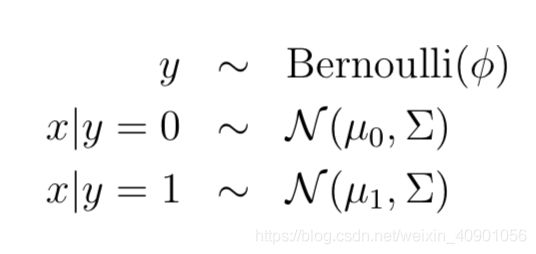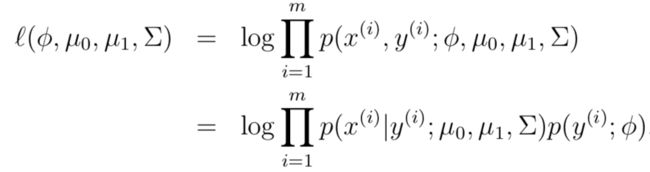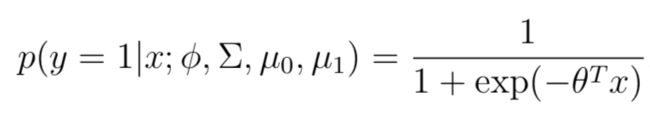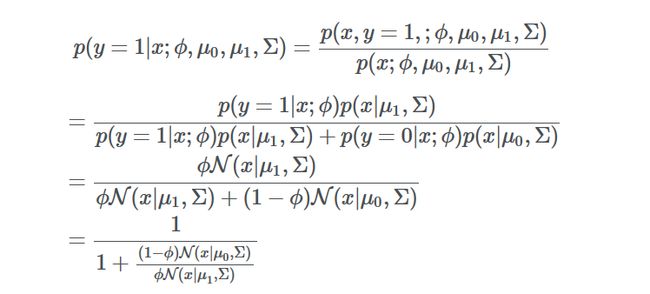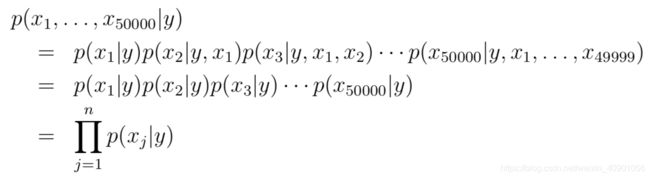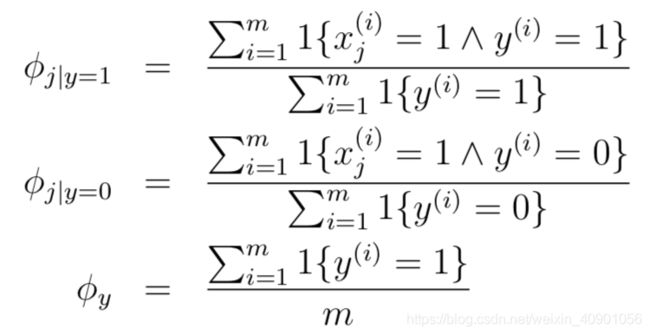Andrew Ng Stanford机器学习公开课 总结(5) Lecture 5 高斯判别分析和朴素贝叶斯

如果图片不完成请参考git page原文

Lecture 5 高斯判别分析和朴素贝叶斯

介绍Gaussian Discriminant Analysis以及Naive Bayes

生成式学习 Generative Learning algorithm

关键词：Generative vs Discriminative

判别式算法 Discriminative learning algorithm

如逻辑回归、决策树、SVM等常见算法都是直接对p(y|x;θ)进行建模，这类算法叫做判别式发算法(Discriminative learning algorithm)。以二分类的逻辑回归为例，对于给定的一组动物的特征数据，需要我们对数据进行分类：y=1代表大象、y=0代表狗。那么分类算法（如lr）要做的就是找到一个决策边界（在一维空间就是一条线），之后对于一条数据，根据该数据在决策边界的哪一边，来判断该动物是狗还是大象。

Discriminative learning algorithm的重点在于找到一个映射mapping，从x->y的映射，这样可以根据特征x判断类别y。

生成式学习 Generative Learning algorithm

生成式算法与判别式算法相反，首先给出根据一群大象，之后算法对大象的特征分布建模，即学习大象长什么样。同理，给我们一群狗，算法对狗的特征分布进行建模。因此，实际上生成式算法是对p(x|y;θ)建模。因此，p(x|y = 0)表示狗的特征分布，p(x|y = 1)表示大象的特征分布。

那么，那么用特征分布来对样本分类呢，答案是贝叶斯定理（Bayes rule）。根据贝叶斯rule：

其中p(y)叫做先验分布（class priors），根据概率公式不难得出p(x) = p(x|y = 1)p(y = 1) + p(x|y = 0)p(y = 0)，但其实预测分类的时候，根本用不到p(x)，因为对于某个样本来说，不非是比较p(y=0|x)和p(y=1|x)的大小，根据大小判断样本所属类别，其中p(x)是比较项的公共分母，因此可以直接去掉，不影响大小关系。用公式表达就是：

1. 高斯判别分析 Gaussian discriminant analysis

Gaussian discrim- inant analysis (GDA)高斯判别分析就是生成式算法的一种。GDA假设p(x|y)服从多元正态分布。

1.1 多元正态分布 The multivariate normal distribution

多元正态分布也叫多元高斯分布multivariate Gaussian distribution，对于n-dimendions的多元高斯分布 参数为：均值向量 μ ∈ Rn 以及协方差矩阵 Σ ∈ Rn×n, 其中 Σ ≥ 0 即半正定。因此N(μ, Σ)的概率密度为：

]

其中，|Σ|代表矩阵Σ的行列式。对于服从N(μ, Σ)分布的随机变量X，均值μ为：

在概率论中，协方差公式可以表示为:

因此，对于任意 X ∼ N (μ, Σ)必然能够推导出Cov(X) = Σ。

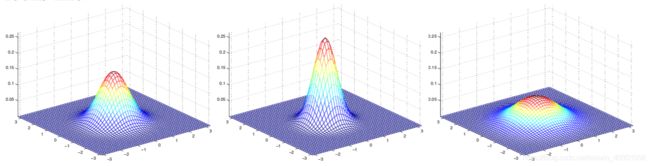
以上是对于公式的基本解释，下面利用图像加深理解：二维(2-dimension)的高斯分布

因为是二维的高斯，因此均值μ是21的向量，而协方差Σ是22的矩阵。其中最左边的是标准正态分布，也就是μ=[0,0] 0均值, Σ=I=[[1,1],[1,1]]单位矩阵；中间的依旧是0均值，但是Σ = 0.6I；最右侧的Σ = 2I。因此不难看出，随着Σ变大 高斯分布变得更矮更胖(spread-out and compressed)。具体分布例子，可以参考原讲义。

1.2 高斯判别分析模型 The Gaussian Discriminant Analysis model

对于分类问题，y∈{0,1}代表标签，随机变量x代表输入特征，利用GDA对p(x|y)建模：

其中标签y∈{0,1}因此服从伯努利(Bernoulli)分布，对于y给定的情况下，条件概率p(x|y=0 or 1)服从高斯分布，这就是GDA的基本假设。更详细的分布公式如下：

通常情况下，模型采用两个均值向量μ0 和 μ1，但是协方差矩阵采用同一个Σ。

模型参数包括：φ, Σ, μ0, μ1。φ表示y=1的概率，那么(1-φ)表示y=0的概率。因此 log似然函数(log-likelihood)为：

通过最大化似然估计，可以推导出各个参数的估计为：这里只给出结果，如果想了解具体推导过程，请参考博客。

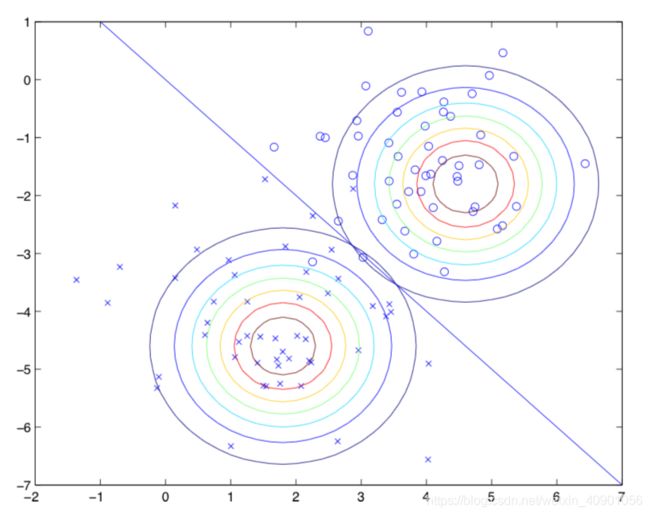
为了更好的直观理解，请看下图：

图中圆圈代表正样本，叉号代表负样本，直线p(y = 1|x) = 0.5代表分类边界(decision boundary)。因为Σ相同所以两个形状相同，但是具有不同的μ 。

1.3 高斯判别分析 VS 逻辑回归

逻辑回归LR请参考我的另一篇文章

首先说结论：对于GDA的概率分布p(y = 1|x; φ, μ0, μ1, Σ)，如果将其看作针对变量x的函数的话，那么p可以表示成逻辑函数的形式：其中θ是φ,Σ,μ0,μ1的函数。

与LR的形式完全一样，但是这个形式是怎么来的呢：根据上文p(x|y=1)和p(x|y=0)服从相同协方差的高斯分布，可以得到如下推导

由于高斯分布属于指族，因此公式下面的比例部分可以转化成 exp(θTx)的形式，其中θ是φ,Σ,μ0,μ1的函数。

结论：如果p(x|y)服从多元高斯分布(相同Σ)，那么p(y|x)就一定是逻辑函数；其实对于x|y服从泊松分布，即p(x|y=0) ∼ Poisson(λ0), p(x|y=1) ∼ Poisson(λ1)，同样可以得出p(y|x)是逻辑函数。但是反过来都是不成立的，也就是y|x服从逻辑分布，并不能得出x的分布是高斯还是柏松。

因此，GDA和LR的区别为：

• GDA带有更强的假设，对数据要求更高，因为要求数据服从高斯分布。而LR更加普世，不在乎数据的分布，不论是数据服从高斯还是柏松，LR都可以得到很好的结果。当然，如果数据确实服从多元高斯分布，那么GDA效果会更加好。
• 同时GDA需要的数据量也要远小于LR，少量数据就可以得到不错的结果。
• 工业界LR更为常用，因为不用考虑x的分布，同时LR更加简单，具有较好的解释性。

---

2. 朴素贝叶斯 Naive Bayes

2.1. 介绍

上文的GDA，特征x是连续向量。而对于离散值的特征，显然无法利用高斯分布的假设，那么GDA也就无从谈起。这时Naive Bayes(NB)就应运而生了。

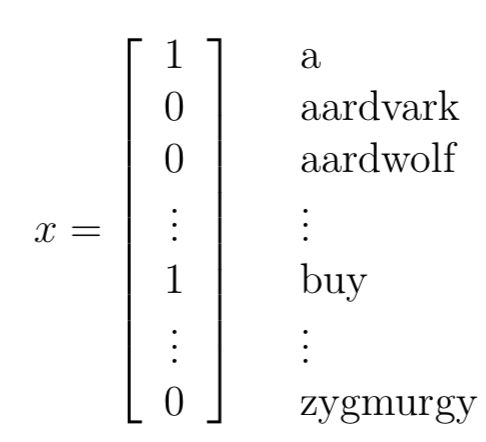
首先考虑一个邮件分类的例子：一封email会包含很多单词，这些单词就是特征，我们要做的就是对邮件进行分类，y=1代表垃圾邮件，y=0代表正常邮件。那么问题来了，特征x到底怎么表示呢，一种通用的方法就是one-hot，如下：

向量的长度就是词表的大小，值表示该单词是否在该邮件中出现过，1表示出现过。如果词表大小是5000，那么x就是5000-dimensional的{0,1}向量。对于生成式模型，我们必须对p(x|y)建模，如果利用多项式分布(multinomial distribution)对x建模，那么参数规模为(2^50000 −1)-dimensional参数向量。显然参数规模太大。因此NB提出了一个朴素贝叶斯假设(Naive Bayes assumption)来解决这个问题。

2.2. 模型

条件独立假设：给定y的情况下，x1和x2是独立的，即p(x1|y) = p(x1|y, x2)。注意与p(x1) = p(x1|x2)不同，这表示任何情况都独立。与NB假设不一样，尤其注意。

条件独立假设的直观解释就是，例如buy是词表中第2087个词，第price是词表中第39831个词，那么如果给定我们y=1也就是这是个垃圾邮件的情况下，是否出现buy与是否出现price是独立的，即 p(x2087|y) = p(x2087|y, x39831)。根据条件独立假设，那么公式可以改写成：

其实这个假设在多数情况下是不成立的，但是真是应用中，即便假设不成立，但是NB模型依旧可以取得不错效果。我们将模型参数简化表示为：

• φj|y=1 = p(xj = 1|y = 1)
• φj|y=0 = p(xj = 1|y = 0)
• and φy = p(y = 1)

给定m个训练样本，那么样本表示为：{(x(i),y(i));i = 1, . . . , m}，因此似然函数如下：

最大化上述函数，可以得出如下结果：只给出结果，推导过程并不难

公式中的“∧”代表“且”。上述结果符合我们的直观理解：φj|y=1就是垃圾邮件中词语j出现的比例，φj|y=0同理，φy就是样本中垃圾邮件的比例。

2.3. 预测

对于给定一个特征x，怎样预测y=0还是1呢？答案就是贝叶斯公式，与GDA类似，计算给定x的情况下，y=1的概率大小：

对于连续值，我们也可以先将其离散化，之后采用NB的方法。

2.4. 拉普拉斯平滑 Laplace smoothing

如果词语在我们之前的训练样本中没有出现过，那么p(x=|y=0)和p(x=|y=1)都等于0，因此计算p(y|x)=0/0，无法计算。Laplace smoothing目的就是解决这个问题，因此公式有所变化：

参考

• GDA数学推导
• 网易公开课
• 课程主页
• 课程笔记