计算机视觉与深度学习-卷积&图像去噪&边缘提取

1 图像去噪与卷积

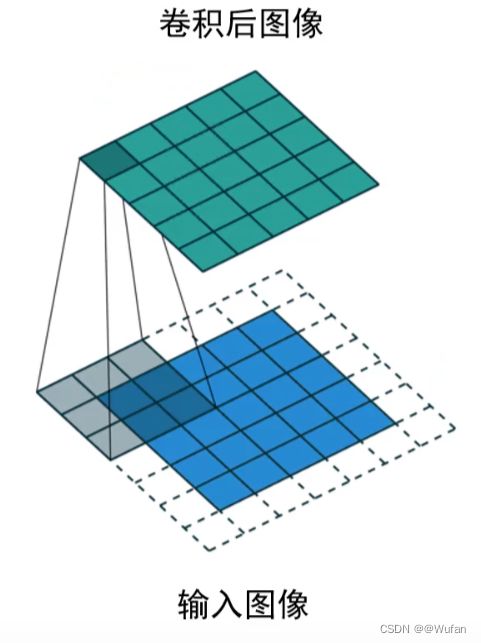
1.1 卷积定义

卷积的定义：令F为图像，H为卷积核,F与H的卷积记为R = F * H
R${}_{ij}$ = $\sum _{u,v}$H${}_{i-u,j-v}$F${}_{u,v}$

1.2 卷积性质

• 叠加性：filter(f${}_1$ + f${}_2$)=filter(f${}_1$)+filter(f${}_2$)
• 平移不变性： filter(shift(f))=shift(filter(f))
• 交换律：a * b = b * a
• 结合律：a * (b * c) = (a * b) * c
• 分配律：a * (b + c) = (a * b) + (a * c)
• 标量：ka * b = a * kb = k(a * b)

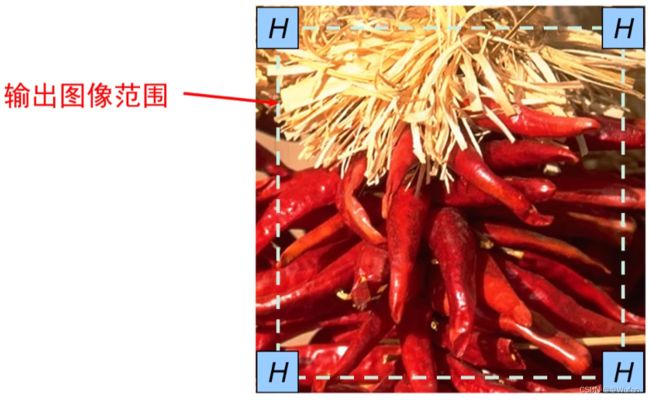
1.3 边界填充

---

---

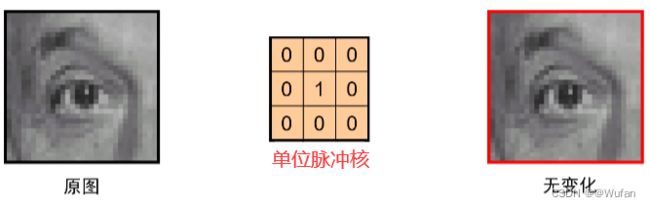
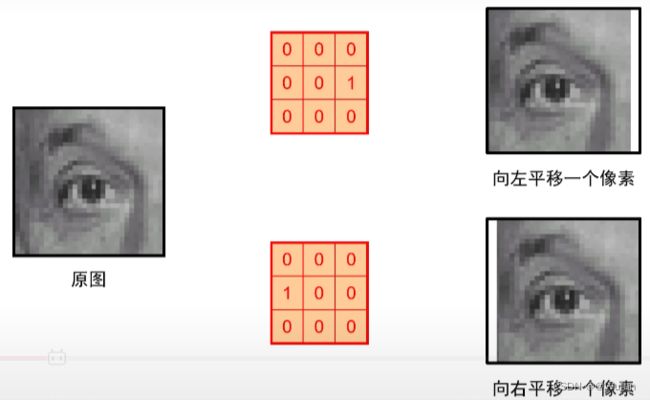
1.4 卷积示例

---

---

---

---

---

1.5 小结

• 卷积操作后的图像要小于输入时图像，通过边界填充，我们可以实现卷积前后图像的尺寸不变；
• 一种最常用的边界填充就是常数填充。

2 高斯卷积核

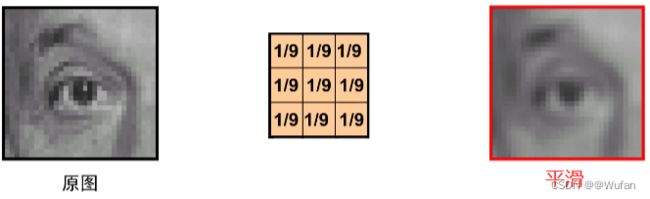
2.1 平均卷积核存在的问题

振铃：卷积后的图像产生了一些水平和垂直方向的条状

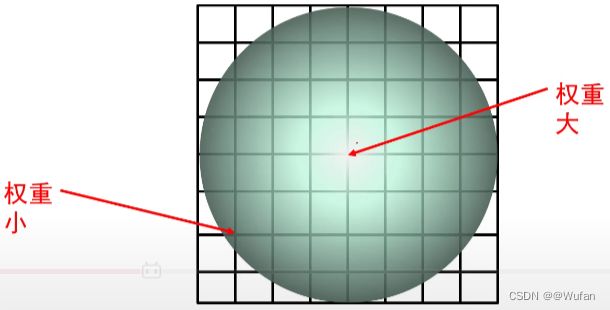
2.2 平均卷积核的解决方法

：根据领域像素与中心的远近程度分配权重

2.3 高斯卷积核的生成步骤

1）确定卷积核的尺寸，比如5 * 5
2）设置高斯函数的标准差，比如$\sigma$ = 1
$G_{\sigma }$ = $\frac{1}{2\pi {\sigma }^2}$$e^{-\frac{x^2+y^2}{2{\sigma }^2}}$
3）计算卷积核各个位置权重值
4）对权重值进行归一化

---

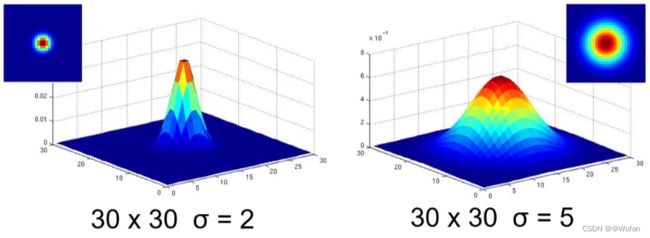
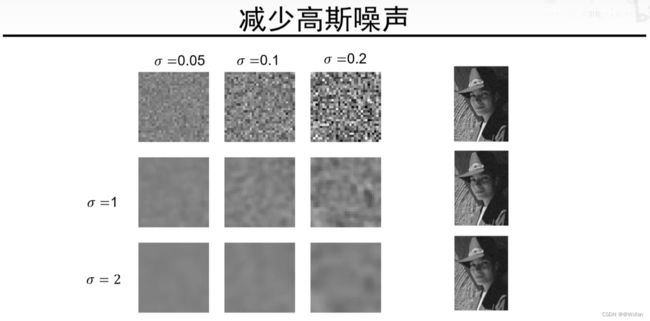
2.4 高斯卷积核的参数设置

1）卷积核的尺寸

模板尺寸越大，平滑效果越强

2）高斯函数的标准差

方差越大，平滑效果越明显

2.5 高斯卷积核的参数小结

• 大方差或者大尺寸卷积核平滑能力强
• 小方差或者小尺寸卷积核平滑能力弱
• 经验法则：将卷积核的半窗宽度设置为3$\sigma$，最终卷积模板尺寸为2 * 3$\sigma$ + 1
  例：标准差设置成1，卷积模板宽度=231 + 1 = 7

2.6 高斯卷积核 vs. 平均卷积核

2.7 高斯卷积核

• 去除图像中的“高频”成分（低通滤波器）
• 两个高斯卷积核卷积后得到的还是高斯卷积核
  • 使用多次小方差卷积核连续卷积，可以得到与大方差卷积核相同的结果
  • 使用标准差为 $\sigma$ 的高斯核进行两次卷积与使用标准差$\sigma \sqrt{2}$的高斯核进行一次卷积相同
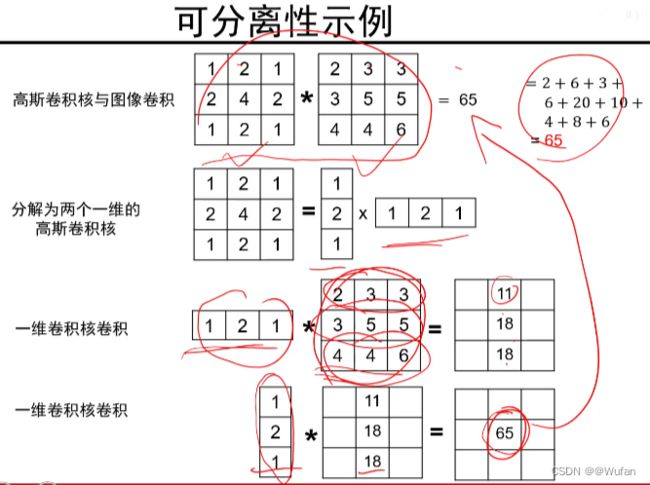
• 可分离
  • 可分解为两个一维高斯的乘积
    

2.8 卷积操作运算量

1）用尺寸为m * m的卷积核卷积一个尺寸为n * nd的图像，其计算复杂度是多少？
答：O($n^2{m}^2$)
2）如果核可分离呢？
答：O($n^{2}m$)

1.2.8 小结

高斯卷积核，它能够有效地抑制噪声、实现图像平滑。同时，高斯卷积核的堆叠以及分解，都可以用于减少卷积计算的复杂度。

3 图像噪声与滤波器

3.1 噪声

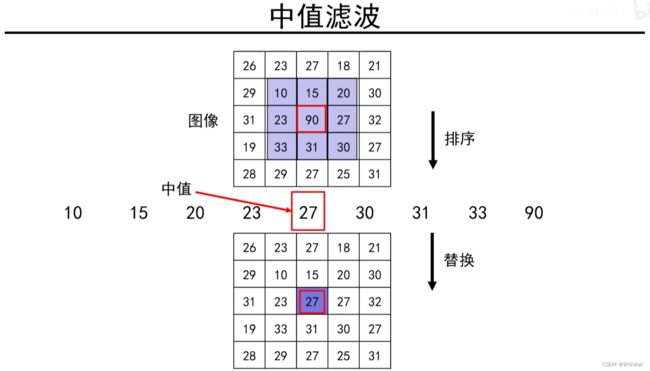
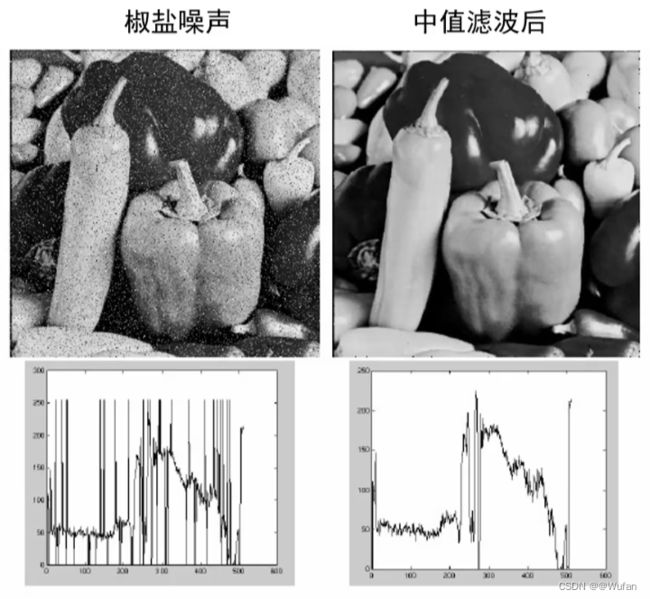
1）椒盐噪声：黑色像素和白色像素随机出现，建议使用中值滤波。
2）脉冲噪声：白色像素随机出现，建议使用中值滤波。
3）高斯噪声：噪声强度变化服从高斯分布（正态分布），建议使用高斯卷积核去噪。

3.1.1 椒盐噪声

---

---

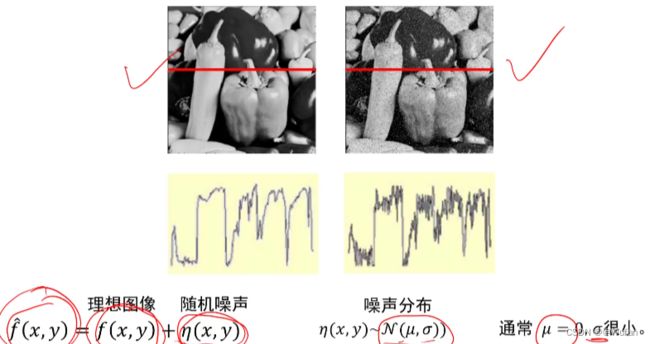
3.1.2 高斯噪声

---

4 卷积与边缘提取

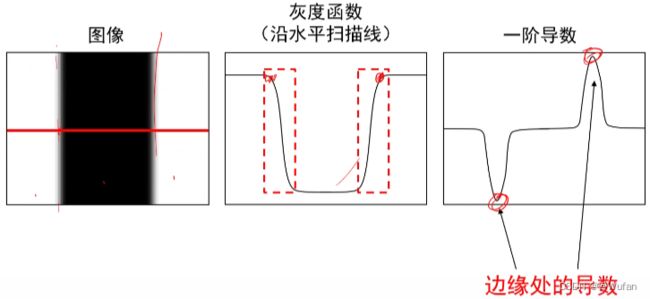
4.1 什么是边缘

图像中亮度明显而急剧变化的点

4.2 为什么要研究边缘

1）编码图像中的语义与形状信息
2）相对于像素表示，边缘表示显然更加紧凑

4.3 边缘的种类

4.4 边缘检测

图像中亮度明显而急剧变化的地方

4.5 图像求导

2D函数f(x,y)的偏导为：
$\frac{\partial f(x,y)}{\partial x}$ = ${\lim }_{x\to \epsilon }$$\frac{f(x+\epsilon ,y)-f(x,y)}{\epsilon }$

图像求导公式：
$\frac{\partial f(x,y)}{\partial x}$ ≈ $\frac{f(x+1,y)-f(x,y)}{1}$

4.6 图像梯度

1）图像梯度：$▽f$ = [ $\frac{\partial f}{\partial x}$ , $\frac{\partial f}{\partial y}$ ] 梯度指向灰度变化最快的方向

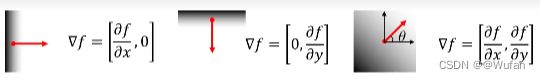
2）梯度方向：$\theta$ = $ta{n}^{-1}$$(\frac{\partial f}{\partial y}/\frac{\partial f}{\partial x})$
3）梯度的模：||$▽f$|| = $\sqrt{(\frac{\partial f}{\partial x}{)}^2+(\frac{\partial f}{\partial y}{)}^2}$

4.7 噪声的影响

1）噪声带来的边缘检测问题
噪声图像的某一行或列的灰度值随位置变换的情况

---

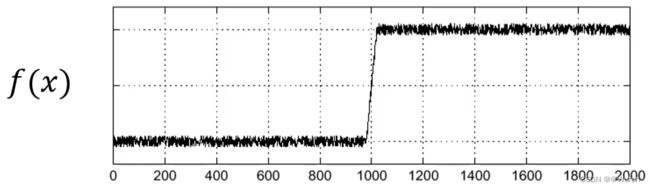
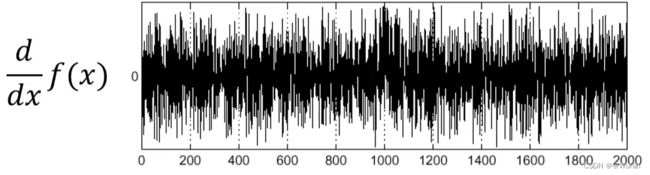
边缘在什么位置？
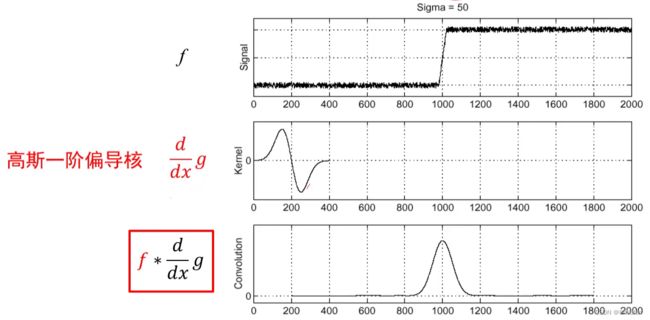
2）解决方法：先平滑再求导

3）解决方法：先求导再卷积(节省了一次图像卷积操作)
微分是卷积，而卷积具有结合性
$\frac{d}{dx}(f\ast g)$ = f * $\frac{d}{dx}g$

4）高斯一阶偏导卷积核

5）高斯一阶偏导卷积核的方差变化

$\sigma$越大，提取的轮廓越粗犷
$\sigma$越小，提取的轮廓越细致

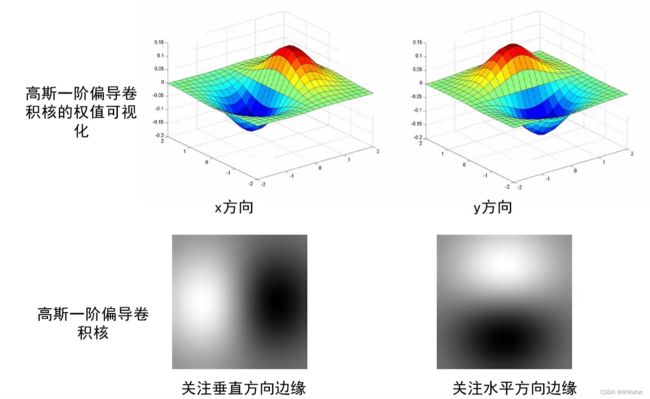
4.8 高斯核 vs. 高斯一阶偏导核

• 高斯核
  • 消除高频成分（低通滤波器）
  • 卷积核中的权值不可为负数
  • 权值总和为1（恒定区域不受卷积影响）
• 高斯一阶偏导核
  • 高斯的导数
  • 卷积核中的权值可以为负
  • 权值总和是0（恒定区域无响应）
  • 高对比度点的响应值大
    

4.9 边缘检测目标

1）检测目标

2）Canny边缘检测器

① 非极大值抑制

改进：

if（ p 点的梯度强度 > q 点的梯度强度 && p 点的梯度强度 > r 点的梯度强度）：
    p 点保留
else：
    删除 p 点

② 门限过滤

改进：双阈值

③ 总结

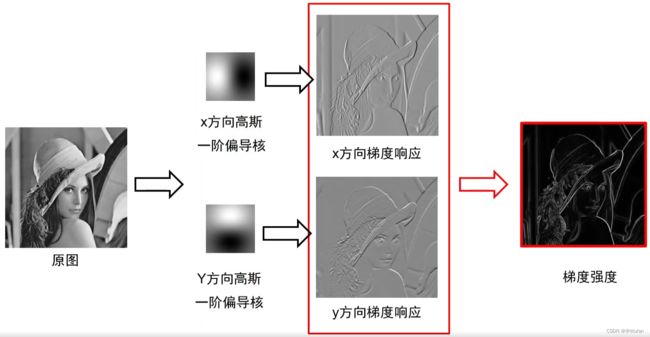
• 用高斯一阶偏导核卷积图像
• 计算每个点的梯度幅值和方向
• 非极大值抑制
  • 将宽的“边缘”细化至单个像素宽度
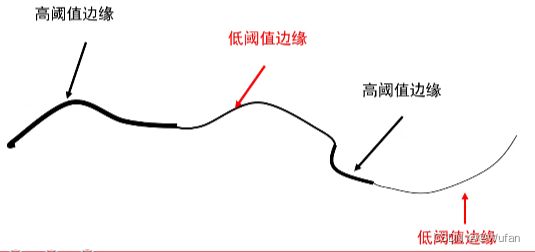
• 连接与阈值（滞后）
  • 定义两个阈值：低和高
  • 使用高阈值开始边缘曲线，使用低阈值继续边缘曲线