c++多模块化划分算法MMM(单链接、全链接、均链接)
文章目录
- 题目1c++代码
- 一、实验目的
- 二、实验描述
-
- 3.1 题目1
-
- 3.1.1 单链接
- 3.1.2 全链接
- 3.1.3 均值链接
- 3.1.4 划分结果统计:
- 3.2 题目2
-
- 3.2.1 单链接
- 3.2.2 全链接
- 3.2.3 均值链接
- 3.2.4 划分结果统计:
- 题目2c++代码
github地址
代码地址
题目1c++代码
#include
distance--;
}
// 如果没有划分成四个模块,则执行MMMSAA
}
if(m <= 4)
{
if(MMMSAA)
{ cout<<"MMMSAA链接划分结果为: "<<endl;
res_print(distance , list);
}
else
{
res_print(distance , list);
if(link_type == 1)
{ cout<<"单链接划分后得到"<<endl;
}
else if(link_type == 2)
{ cout<<"全链接划分后得到"<<endl;
}
else if(link_type == 3)
{ cout<<"均值链接划分后得到"<<endl;
}
res_print(distance , list);
}
break;
}
else
{
MMMSAA = 1;
link_type = 1;
distance = maxLength + 1;
}
}
return list;
}
int JudgeThreshold(vector<vector<int>> &data, vector<int> &first,vector<int> &second,int distance, int link_type)
{
int i,j;
int first_num = first.size();
int second_num = second.size();
//单值
if(link_type == 1)
{
int flag = 0;
for(i = 0; i< first_num; i++)
{
for(j = 0; j < second_num; j++)
{
if( data[first[i]][second[j]] >= distance)
{
flag = 1;
break;
}
if(flag)
break;
}
}
return flag;
}
// 全连接
else if(link_type == 2)
{
int flag = 1;
for(i = 0; i< first_num; i++)
{
for(j = 0; j < second_num; j++)
{
if( data[first[i]][second[j]] < distance)
{
flag = 0;
break;
}
if(!flag)
break;
}
}
return flag;
}
// 均值
else if(link_type == 3)
{
int sum = 0;
double ave = 0;
for(i = 0; i< first_num; i++)
{
for(j = 0; j < second_num; j++)
{
sum += data[first[i]][second[j]];
}
}
ave = sum / (first_num * second_num);
if(ave >= distance)
return 1;
else
return 0;
}
}
// 组合子类
vector<vector<int>> combine(vector<vector<int>> &list, vector<int> &first, vector<int>&second, int second_index, int first_index)
{
vector<vector<int>> res;
vector<int> temp;
int i = 0;
for(i = 0; i< first.size(); i++)
{
temp.push_back(first[i]);
}
for(i = 0; i< second.size(); i++)
{
temp.push_back(second[i]);
}
sort(temp.begin(),temp.begin()+temp.size());
res.push_back(temp);
list.erase (list.begin() + second_index);
list.erase (list.begin() + first_index);
for(i = 0; i < list.size(); i++)
{
res.push_back(list[i]);
}
// sort(res.begin(),res.begin()+res.size());
return res;
}
一、实验目的
编程实现多模块化划分算法MMM(单链接、全链接、均链接)。
全链接
二、实验描述
输入是通信代价、模块数、每个模块最大任务数,输出为划分好的模块,并给出划分代价。
三、 测试结果
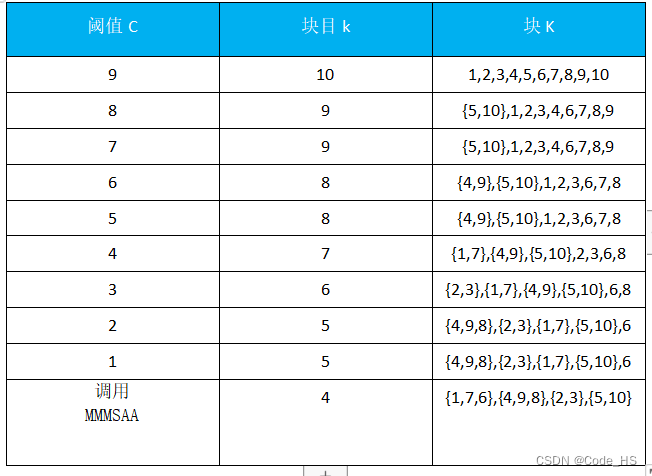
3.1 题目1
使用实现的程序将图1.1 的10个任务划分成4个模块,每个块内任务个数不超过3。
设一智能嵌入式系统,由任务 T1,T2,…,T10 组成,任务间的通信代
价见图 1-1。
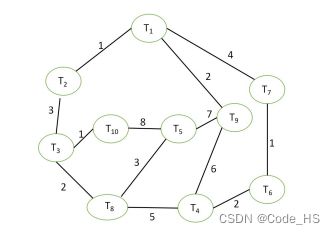
图1-1 任务通信代价图
3.1.1 单链接
3.1.2 全链接
3.1.3 均值链接
3.1.4 划分结果统计:
从划分结果统计来看使用不同链接算法,划分结果是有差异的。单链接的划分代价最小为16,其他俩个划分结果相同,但中间步骤不同。
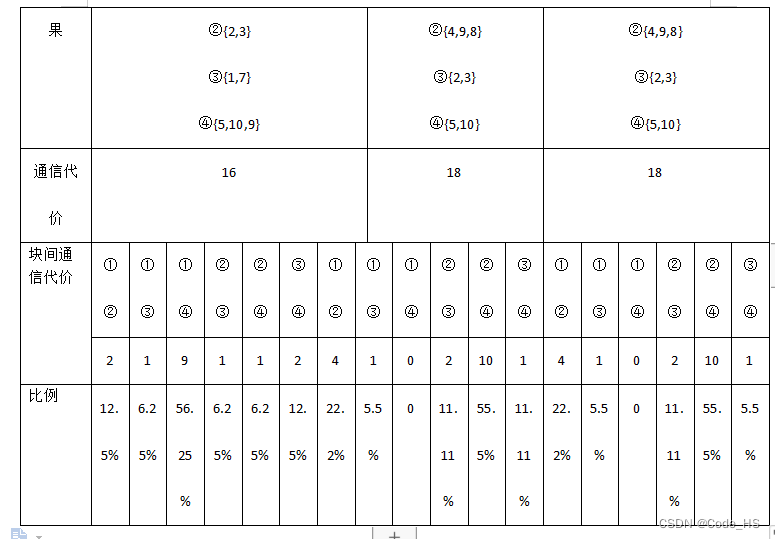
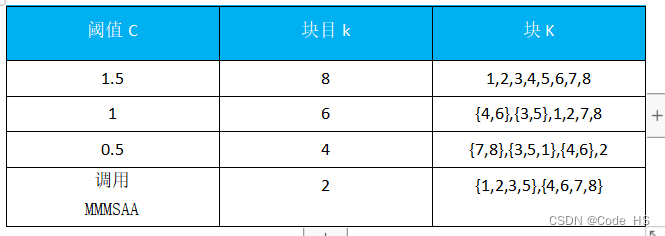
3.2 题目2
图1-2中的8个任务a,b,c,d,f,g,h分成2个模块,每个模块含有4个任务,使得模块间通信代价最小

图1-2 任务通信矩阵
3.2.1 单链接
3.2.2 全链接
3.2.3 均值链接
3.2.4 划分结果统计:
从划分结果统计来看使用不同链接算法,划分结果是有差异的。但此处划分的通信代价相同,都为3。
题目2c++代码
#include
#include
#include
#include
#include
using namespace std;
const int task_num = 8;
vector
vector
vector
int JudgeThreshold(vector
void res_print(int distance, vector
double getMaxDistance(vector
double calculateDistance(vector
#define single
#define Complete
#define Average
int main()
{
double matrix[task_num][task_num] =
{
{0, 0, 0.5, 0, 0.5, 0, 0, 0},
{0, 0, 0.5, 0.5, 0, 0, 0, 0},
{0.5, 0.5, 0, 0.5, 1, 0.5, 0, 0},
{0, 0.5, 0.5, 0, 0, 1, 0, 0},
{0.5, 0, 1, 0, 0, 0.5, 1, 0},
{0, 0, 0.5, 1, 0.5, 0, 0.5, 0.5},
{0, 0, 0, 0, 1, 0.5, 0, 0.5},
{0, 0, 0, 0, 0, 0.5, 0.5, 0},
};//导入通信代价矩阵
vector> data = init(matrix);
vector> tempMatrix = data;
for(int i = 0; i< tempMatrix.size(); i++)
{
for(int j = 0; j< tempMatrix.size(); j++)
{
cout<> list1=Link(data,4,2, 1);//得到经过单连接划分后的list,其中簇中元素最多为4,最多有2个簇
int totalDistance1=calculateDistance(tempMatrix,list1);//计算划分后各簇之间的总通信距离
cout<<"通信距离:"<> list2=Link(data,4 ,2, 2);//得到经过全连接划分后的list,其中簇中元素最多为3,最多有4个簇
int totalDistance2=calculateDistance(tempMatrix,list2);//计算划分后各簇之间的总通信距离
cout<<"通信距离:"<> list3=Link(data, 4, 2, 3);//得到经过均值连接划分后的list,其中簇中元素最多为3,最多有4个簇
int totalDistance3=calculateDistance(tempMatrix,list3);//计算划分后各簇之间的总通信距离
cout<<"通信距离:"< }
vector
{
vector
for(int i = 0; i < task_num; i++)
{
vector temp;
for(int j = 0; j < task_num; j++)
{
temp.push_back(data[i][j]);
}
res.push_back(temp);
}
return res;
}
// 划分结果输出
void res_print(double distance, vector
{
cout<
{
vector temp = list[i];
int length = temp.size();
if(length > 1)
cout<<”{“;
for (int j=0;j < temp.size();j++)
{
cout<
cout<<”,";
}
if(length > 1)
cout<<"}";
if( i != list.size() - 1)
cout<<",";
}
cout<}
double getMaxDistance(vector
{
double max=-1;
int length=task_num;
for (int i = 0; i < length; i++)
{
for (int j = i; j < length; j++)
{
if (data[i][j] >= max)
{
max = data[i][j];
}
}
}
return max;
}
double calculateDistance(vector
{
double totalDistance=0;
//先找到两个相邻的簇,然后匹配簇中的元素
for (int i = 0; i < list.size()-1; i++)
{
vector last= list[i];//得到相邻的簇
for (int j=i+1;j next=list[j];//得到相邻的簇
for (int m=0;m }
vector
{
bool border[task_num][task_num] = {false};//确定该边是否已划分
bool used[task_num] = {false} ;//确定该元素是否已放入簇中
int length=data.size();//矩阵大小
int number=0;//记录簇的个数
int count=0;//计算已经放到簇中的数据个数
vector> list;
// data=getDistance(data);//将通信代价矩阵转换为通信距离矩阵
double maxLength=getMaxDistance(data);//计算通信距离的最大值
//cout<<"maxLength "<
for(int i = 0; i < task_num; i++)
{
vector temp ;
temp.push_back(i);
list.push_back(temp);
}
double distance = maxLength + 0.5;
int m = list.size();
int MMMSAA = 0;
while(1)
{
while(distance > 0 && m > direction)
{
int flag = 0;//是否进行下一轮
for(int i = 0; i < list.size(); i++)
{
vector first = list[i];
for(int j = i + 1; j < list.size(); j++)
{
vector second = list[j];
if(JudgeThreshold(data, first, second,distance, link_type)) //如果均值大于阈值
{
if(first.size() + second.size() <= num)
{
list = combine(list, first, second, j, i);
flag = 1;
}
}
if(flag)
break;
}
if(flag)
break;
}
// res_print(distance, list);
if(flag )
m--;
else
{
if(!MMMSAA)
res_print(distance, list);
//cout<}
int JudgeThreshold(vector
{
int i,j;
int first_num = first.size();
int second_num = second.size();
//单值
if(link_type == 1)
{
int flag = 0;
for(i = 0; i< first_num; i++)
{
for(j = 0; j < second_num; j++)
{
if( data[first[i]][second[j]] >= distance)
{
flag = 1;
break;
}
if(flag)
break;
}
}
return flag;
}
// 全连接
else if(link_type == 2)
{
int flag = 1;
for(i = 0; i< first_num; i++)
{
for(j = 0; j < second_num; j++)
{
if( data[first[i]][second[j]] < distance)
{
flag = 0;
break;
}
if(!flag)
break;
}
}
return flag;
}
// 均值
else if(link_type == 3)
{
double sum = 0.0;
double ave = 0.0;
for(i = 0; i< first_num; i++)
{
for(j = 0; j < second_num; j++)
{
sum += data[first[i]][second[j]];
}
}
ave = sum / (first_num * second_num);
if(ave >= distance)
return 1;
else
return 0;
}
}
// 组合子类
vector
{
vector
vector temp;
int i = 0;
for(i = 0; i< first.size(); i++)
{
temp.push_back(first[i]);
}
for(i = 0; i< second.size(); i++)
{
temp.push_back(second[i]);
}
sort(temp.begin(),temp.begin()+temp.size());
res.push_back(temp);
list.erase (list.begin() + second_index);
list.erase (list.begin() + first_index);
for(i = 0; i < list.size(); i++)
{
res.push_back(list[i]);
}
sort(res.begin(),res.begin()+res.size());
return res;
}