运用逻辑回归进行二分类及多分类

目标：

• 能够清晰理解逻辑回归模型的原理。
• 掌握sigmooid函数的作用
• 能够使用逻辑回归模型实现二分类以及多分类任务

知识要点

一、逻辑回归模型

模型简介：

逻辑回归实际上是一个分类算法，其应用于对样本数据进行分类的场景中。例如，给定如下的鸢尾花数据集：

花萼长度	花萼宽度	花瓣长度	花瓣宽度	类别
5.4	3.9	1.3	0.4	山鸢尾
5.1	3.5	1.4	0.3	山鸢尾
5.8	2.7	4.1	1.0	杂色鸢尾
6.2	2.2	4.5	1.5	杂色尾
6.3	2.5	5.0	1.9	维吉尼亚鸢尾
6.5	3.0	5.2	2.0	维吉尼亚鸢尾
5.6	3.1	3.8	0.7	？

我们就可以基于一致的数据集，建立模型，从而对位置的样本数据进行预测。

算法的分类思想

逻辑回归实现分类的思想：将每条样本进行‘打分’，然后设置一个阈值，达到这个阈值的，分为一个类别，没有达到这个阈值的，分为另外一个类别。对于阈值，划分为哪个类别都可以，但是，要保证阈值划分的一致性。

算法模型

对于逻辑回归，模型的前面于线性回归类似：

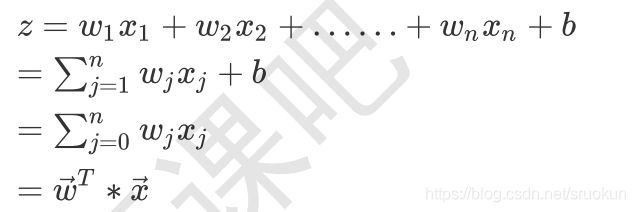
不过，Z的值是一个连续的值，取值方位为（－∞，+∞），我们可以将阈值设置为中间的位置，也就是0，当Z>0时，模型将样本判定为一个类别（正例），Z≦0时，模型将样本判定为另一个类别（负例），这样模型就实现了二分类任务。

sigmoid函数

函数原型

对于分类任务来说，如果仅仅给出分类的结果，在某些场景下，提供的信息可能并不充足，这就会带来一定的局限。因此，我们建立分类模型，不仅应该能够进行分类，同时，也应该能够提供样本属于该类别的概率。这在现实中非常使用。例如，某人患病的概率，明天下雨的概率等。
因此，我们需要将Z值转换为概率值，逻辑回归使用sigmoid函数来实现转换，该函数的原型为：

当Z的值从-∞向+∞过渡时，sigmoid函数的取值范围为(0，1)，这正好是概率的取值范围，当Z=0时，sigmoid(0)的值为0.5. 因此，模型就可以将sigmoid的输出值p作为正例的概率，而1一p作为负例的概率。以阈值0.5作为两个分类的阅值，就是看p与1 一p哪个类别的概率值更大，预测的结果就为哪个类别。
假设真实的分类y的值为1与0，则：

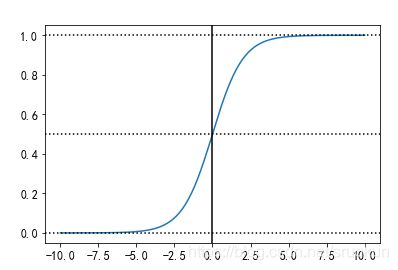
sigmoid函数图像

现在我们通过Python程序来绘制sigmoid函数在[-10，10]区间的图像。

import numpy as np
import matplotlib.pyplot as plt 

plt.rcParams["font.family"] = "SimHei"
plt.rcParams["axes.unicode_minus"] = False
plt.rcParams["font.size"] = 12

#定义sigmoid函数。
def sigmoid(z):
	return 1/(1+ np.exp(-z))

z = np.linspace(-10, 10, 200)
plt.plot(z, sigmoid(z))
#绘制水平线与垂直线。
plt.axvline(x=0, ls="-", c="k")
plt.axhline(ls=":", c="k")
plt.axhline(y=0.5, ls=":", c="k")
plt.axhline(y=1, ls=":", c="k")
p1t.x1abel("z值")
plt.y1abel("sigmoid(z)值")
Text(0, 0.5, 'sigmoid(z)值')

参数求解

与线性回归类似，逻辑回归模型的关键之处，就是要求解出模型的参数，也就是 与 的值，一旦参数值 确定，我们就能够对未知样本数据进行预测。
刚才，我们已经得出了逻辑回归损失函数，只需要在该函数上进行优化即可。我们可以采用对损失函数 求导（梯度），然后通过梯度下降的方式来求解。

二、逻辑回归实现二分类

模型训练与预测

我们以鸢尾花数据集为例，演示通过逻辑回归算法实现二分类。

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
import warnings

warnings.filterwarnings("ignore")

iris = load_iris()
X, y= iris.data,iris.target
#因为或尾花具有三个类别，4个特征，此处仅使用其中两个特征，并且移除一个类别(类别0)
X= X[y!=0, 2:]
y= y[y!=0]
#此时，y的标签为1与2,我们这里将其改成0与1，(仅仅足为了习惯而已)
y[y == 1]= 0
y[y == 2]= 1

X_train, X_test, y_train, y_test= train_test_split(X,y,test_size=0.25,random_state=2)
lr = LogisticRegression()
lr.fit(X_train, y_train)
y_hat = lr.predict(X_test)
print("权重: ",lr.coef_)
print("偏置: " ,lr.intercept_)
print("真实值: ",y_test)
print("预测值:",y_hat)

权重: [[-0.12107795 2.34770742]]
偏置: [-3.03870143]
真实值: [1 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 1 0 0 1 0 1]
预测值: [0 0 1 0 0 0 0 1 0 0 1 1 1 0 0 0 0 0 1 1 1 0 0 0 1]

结果可视化

现在，我们对分类的结果进行可视化显示。首先，我们来绘制下鸢尾花数据的分布图。

c1 = X[y == 0] 
c2 = X[y == 1] 
plt.scatter(x=c1[:, 0], y=c1[:, 1], c="g", label="类别0") 
plt.scatter(x=c2[:, 0], y=c2[:, 1], c="r", label="类别1") 
plt.xlabel("花瓣长度") 
plt.ylabel("花瓣宽度") 
plt.title("鸢尾花样本分布") 
plt.legend()

接下来，我们来绘制在测试集中，样本的真实类别与预测类别。

plt.figure(figsize=(15, 5)) 
plt.plot(y_test, marker="o", ls="", ms=15, c="r", label="真实类别") 
plt.plot(y_hat, marker="X", ls="", ms=15, c="g", label="预测类别") 
plt.legend() 
plt.xlabel("样本序号") 
plt.ylabel("类别") 
plt.title("逻辑回归分类预测结果") 
plt.show()

计算概率值

之前我们讲过，作为分类模型，不仅能够预测样本所属的类别，而且，还可以预测属于各个类别的概 率。这在实践中是非常有意义的。接下来，我们就来求解逻辑回归预测的概率值。

# 获取预测的概率值，包含数据属于每个类别的概率。 
probability = lr.predict_proba(X_test) 
display(probability[:5]) 
display(np.argmax(probability, axis=1))
# 产生序号，用于可视化的横坐标。 
index = np.arange(len(X_test)) 
pro_0 = probability[:, 0] 
pro_1 = probability[:, 1] 
tick_label = np.where(y_test == y_hat, "O", "X") 
plt.figure(figsize=(15, 5)) 
# 绘制堆叠图 
plt.bar(index, height=pro_0, color="g", label="类别0概率值") 
# bottom=x，表示从x的值开始堆叠上去。 
# tick_label 设置标签刻度的文本内容。 
plt.bar(index, height=pro_1, color='r', bottom=pro_0, label="类别1概率值", tick_label=tick_label) 
plt.legend(loc="best", bbox_to_anchor=(1, 1)) 
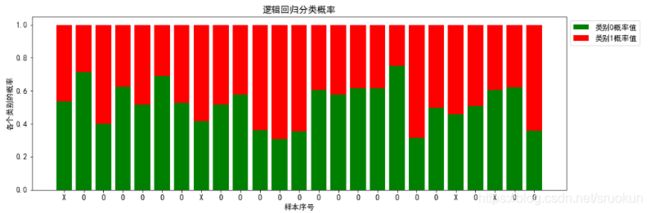
plt.xlabel("样本序号") 
plt.ylabel("各个类别的概率") 
plt.title("逻辑回归分类概率") 
plt.show()

array([[0.5336087 , 0.4663913 ],
[0.71429158, 0.28570842],
[0.39949963, 0.60050037],
[0.6241773 , 0.3758227 ],
[0.51549281, 0.48450719]])
array([0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0,0, 0, 1], dtype=int64)

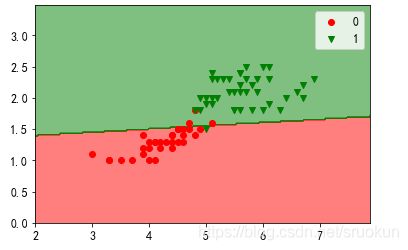
绘制决策边界

我们可以绘制决策边界，将分类效果进行可视化显示。首先，我们来定义绘制决策边界的函数。

from matplotlib.colors import ListedColormap
# 定义函数，用于绘制决策边界。 
def plot_decision_boundary(model, X, y): 
    color = ["r", "g", "b"] 
    marker = ["o", "v", "x"] 
    class_label = np.unique(y) 
    cmap = ListedColormap(color[: len(class_label)]) 
    x1_min, x2_min = np.min(X, axis=0) 
    x1_max, x2_max = np.max(X, axis=0) 
    x1 = np.arange(x1_min - 1, x1_max + 1, 0.02) 
    x2 = np.arange(x2_min - 1, x2_max + 1, 0.02) 
    X1, X2 = np.meshgrid(x1, x2) 
    Z = model.predict(np.array([X1.ravel(),X2.ravel()]).T).reshape(X1.shape) 
# 绘制使用颜色填充的等高线。 
    plt.contourf(X1, X2, Z, cmap=cmap, alpha=0.5) 
    for i, class_ in enumerate(class_label): 
        plt.scatter(x=X[y == class_, 0], y=X[y == class_, 1], 
                c=cmap.colors[i], label=class_, marker=marker[i])
    plt.legend()
    plt.show()

plot_decision_boundary(lr, X_train, y_train)

我们再来绘制模型在测试集上的划分效果。

plot_decision_boundary(lr, X_test, y_test)

三、逻辑回归实现多分类

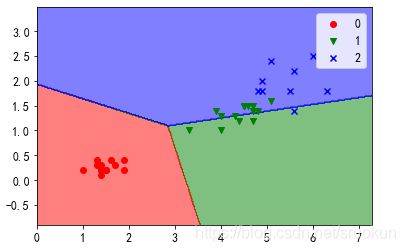
建模与可视化

逻辑回归算法也可以实现多分类任务。

iris = load_iris() 
X, y = iris.data, iris.target 
# 仅使用其中的两个特征。 
X = X[:, 2:] 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0) 
lr = LogisticRegression() 
lr.fit(X_train, y_train) 
y_hat = lr.predict(X_test) 
print("分类正确率：", np.sum(y_test == y_hat) / len(y_test))

分类正确率： 0.6578947368421053

# 训练集决策边界 
plot_decision_boundary(lr, X_train, y_train)

# 测试集决策边界 
plot_decision_boundary(lr, X_test, y_test)

多分类实现细节（扩展）

我们刚才使用逻辑回归模型成功实现了多分类，不过，我们可能会有如下疑问： 在我们之前的讲解中，逻辑回归模型是依靠sigmoid函数的值来判别数据的类别的，判别的依据是：

这就是说，逻辑回归应该只能实现二分类，可是，刚才的程序中，也完全实现了多分类的效果，而且在 程序中，并没有提现出明显的不同，那么，多分类是怎样做到的呢？
多分类在实现上，可以采用两种方式：

• one versus rest（一对其他）：
  假设有三个类别A、B、C，而逻辑回归判断Z>0,P值大于0.5属于一个类别；Z<0，P值小于0.5属于另一个类别；
  三个类别怎么做呢，可以创建多个模型实现是或不是的分类，是于不是永远是二分类。
  我们创建三个模型分别为：
  是A，不是A
  是B，不是B
  是C，不是C
  由此得出各自的概率（A/（A+B+C）），从而对三个类别进行分类。
• multinomial（多项式）
  类似于神经网络的操作，它会输出多个Z的值，同时有各自的权重。
  这样ABC就有Z1,Z2,Z3,再使用softmax对Z值进行转换，因为这里Z值是有正有负的，
  不能使用Z1/（Z1+Z2+Z3）来计算概率，我们采取以e为底指数为Z值来代替Z，最后计算概率进行分类。