7 一阶逻辑推理（11.23，11.30）

1 一阶谓词逻辑推理基础

1.1 谓词公式的解释

谓词的定义：设D是论域，P：Dⁿ→{T，F｝是一个映射，其中：

则称P是一个n元谓词，记为P(x₁,x₂,…,x_n)，其中，x₁,x₂,…,x_n为个体，可以是个体常量、变元和函数。

确定谓词公式P(x,y) ∧Q(x,y)的真值（x,y∊ [1,2]），需要事先知道以下内容：

在个体域中，谓词公式的真值可能为T也可能为F。上表只是一种可能的情况。在实际情况下，需要根据事实规定某个式子是真或假。

谓词公式中包含谓词，以及个体常量、变元或函数，这些量还存在个体域，因此：

谓词公式的真值：

• 个体常量和函数在个体域上的取值（值指派）
• 为谓词指派真值（谓词真值指派）

谓词公式在个体域上的一个解释就是——对谓词公式中的个体常量、函数和谓词进行赋值。

定义1： 设D是谓词公式P的非空个体域，若对P中的个体常量、函数和谓词按如下规定赋值，则称这些指派为P在D上的一个解释I ：

(1) 为每个个体常量指派D中的一个元素； 为每个n元函数指派一个从Dⁿ到D的一个映射，其中Dⁿ ={(x₁, x₂, …, x_n)| x₁, x₂, …, x_n∈D} （值指派）

(2) 为每个n元谓词指派一个从Dⁿ到{F，T}的映射。（谓词真值指派）

结论：由上面的例子可以看出，谓词公式的真值是针对某一个解释而言的，它可能在某一个解释下真值为T，而在另一个解释下为F。由此，我们可以引出谓词公式的永真性、永假性、可满足性等概念。

1.2 谓词公式的永真性和可满足性

定义2：谓词公式的永真性：如果谓词公式P对非空个体域D上的任一解释都取得真值T，则称P在D 上是永真的；如果P在任何非空个体域上均是永真的，则称P永真。

定义3：谓词公式的可满足性：对于谓词公式P，如果至少存在D上的一个解释，使公式P在此解释下的真值为T，则称公式P在D上是可满足的。谓词公式的可满足性也称为相容性。

定义4：谓词公式的永假性：如果谓词公式P对非空个体域D上的任一解释都取真值F，则称P在D上是永假的；如果P在任何非空个体域上均是永假的，则称P永假。谓词公式的永假性又称不可满足性或不相容。

1.3 谓词公式的等价性和永真蕴含性

谓词公式的等价式可定义如下：

定义5：设P与Q是D上的两个谓词公式，若对D上的任意解释，P与Q都有相同的真值，则称P与Q在D上是等价的。如果D是任意非空个体域，则称P与Q是等价的，记作P⇔ Q。

(1) 双重否定律：¬ ¬ P ⇔ P
(2) 交换律：(P∨ Q) ⇔ (Q∨ P)， ( P∧ Q) ⇔ ( Q∧ P)
(3) 结合律：(P∨ Q)∨ R ⇔ P∨ (Q∨ R) ，(P∧ Q)∧ R ⇔ P∧ (Q∧ R)
(4) 分配律：P∨ (Q∧ R) ⇔ (P∨ Q)∧ (P∨ R)，P∧ (Q∨ R) ⇔ (P∧ Q)∨ (P∧ R)
(5) 摩根定律：¬ (P∨ Q) ⇔ ¬ P∧ ¬ Q，¬ (P∧ Q) ⇔ ¬ P∨ ¬ Q
(6) 吸收律：P∨ (P∧ Q) ⇔ P，P∧ (P∨ Q) ⇔ P
(7) 补余律：P∨ ¬ P ⇔ T, P∧ ¬ P ⇔ F
(8) 连词化归率：P→Q ⇔ ¬P∨ Q，P↔Q ⇔ (P→Q)∧ (Q→P)，P↔Q ⇔ (P∧ Q)∨ (¬P∧¬Q)
(9) 量词转换率：¬ (∊ x)P ⇔ (∀ x)( ¬ P)，¬ (∀ x)P ⇔ (∊ x) (¬ P)
(10) 量词分配率：(∀ x) (P∧ Q) ⇔ (∀ x)P∧ (∀ x)Q，(∊ x) (P∨ Q) ⇔ (∊ x)P∨ (∊ x)Q

谓词公式的永真蕴涵式可定义如下：

定义6：对谓词公式P和Q，如果P→Q永真，则称P 永真蕴含Q，且称Q为P的逻辑结论，P为Q的前提，记作P ⇒ Q。

常用的永真蕴含式如下：

(1) 化简式 P∧ Q ⇒ P， P∧ Q ⇒ Q
(2) 附加式 P ⇒ P∨ Q， Q ⇒ P∨ Q
(3) 析取三段论 ﹁ P, P∨ Q ⇒ Q
(4) 假言推理 P, P→Q ⇒ Q
(5) 拒取式 ¬Q, P→Q ⇒ ¬P
(6) 假言三段论 P→Q, Q→R ⇒ P→R
(7) 二难推理 P∨ Q, P→R, Q→R ⇒ R
(8) 全称固化 (∀ x)P(x) ⇒ P(y)，其中，y是个体域中的任一个体，依此可消去谓词公式中的全称量词。
(9) 存在固化 (∊ x)P(x) ⇒ P(y)，其中，y是个体域中某一个可以使P(y)为真的个体，依此可消去谓词公式中的存在量词。

1.4 谓词公式的范式

范式是谓词公式的标准形式。

在谓词逻辑中，范式包括前束范式和Skolem范式两种。

前束范式：（1）所有量词均非否定地出现在公式的最前面；（2）所有量词的辖域为整个公式。如：(∀ x) (∀ y) (∊ z)(P(x)∧ Q(y,z)∨ R(x,z))。

Skolem范式：（1）前束范式；（2）所有的存在量词都在全称量词之前。如：(∊ x) (∊ z) (∀ y)(P(x)∨ Q(y,z)∧ R(x,z))。

1.5 置换与合一

在基于谓词的推理过程中，会出现谓词名相同但其个体不同的情况，此时不能直接进行匹配的，需要先进行置换。

在推理过程中，寻找项与项之间的置换，使不同谓词表达式一致的过程叫做合一的过程。

1.5.1 置换

置换是用置换项替换变量。置换项可以是常量、函数或变量。

（1）置换的定义：置换是形如 {t₁/x₁,t₂/x₂,…,t_n/x_n}的有限集合。其中，t₁,t₂,…,t_n是置换项；x₁,x₂,…,x_n是互不相同的变元；t_i/x_i表示用t_i替换x_i。

（2）置换规则：第一：只能用常量、函数或变量置换变量，不能用变量置换常量和函数，不能用常量和函数置换不同的常量和函数；第二：x_i 不能出现在t_i中，如g(x)/x不是置换；第三：不能循环置换，如{y/x, x/y}不是一个置换。

1.5.2 合一

寻找项对变量的合法置换，使两个谓词公式一致。第一：只能用常量、函数或变量置换变量，不能用变量置换常量和函数，不能用常量和函数置换不同的常量和函数；第二：x_i 不能出现在t_i中，如g(x)/x不是置换；第三：不能循环置换，如{y/x, x/y}不是一个置换。

合一的形式定义：

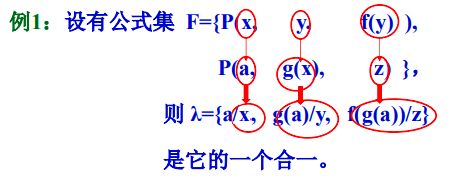
最一般合一：一个公式集的任一合一都可由最一般合一和一个置换的合成置换得到。

定义：设σ是公式集F的一个合一，如果对F的任一个合一θ都存在一个置换λ，使得θ=σ.λ，则称σ是一个最一般合一。

最一般合一的特点与重要性：最一般合一的置换项较少，所产生的例示更一般化，有利于产生新的置换。在推理过程中应尽可能使用最一般合一。

如何判断公式集是否可以合一，又如何找出最一般合一？

最一般合一求取方法——UNIFY算法：

1、用表的形式表示谓词：如谓词P(x, f(y), B)表示为 (P x (f y) B)。

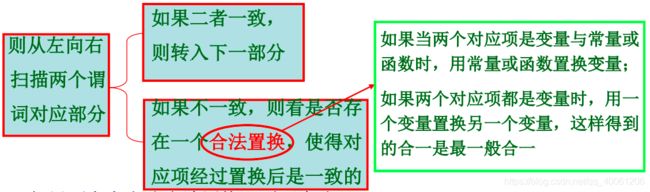
2、判断两个谓词公式能否合一：

第一：如果两个谓词公式的表的长度不同或谓词不同，则不能合一。

第二：如果两个谓词公式的谓词相同，并且表的长度也相同：

如果不存在上述合法置换，则两个公式是不可合一的；如果两个谓词公式经置换达到一致，则两个公式是可合一的。

UNIFY算法不仅可以判断两个公式是否可合一，而且在可合一的情况下，给出它们的最一般合一。

2 自然演绎推理

自然演绎推理是指从一组已知事实出发，直接运用命题逻辑或谓词逻辑中的推理规则推出结论的过程。

自然演绎推理的例子

自然演绎推理的优缺点：

• 优点：定理证明过程自然，易于理解，并且有丰富的推理规则可用。
• 缺点：容易产生知识爆炸，推理过程中得到的中间结论一般按指数规律递增，对于复杂问题的推理不利，甚至难以实现。

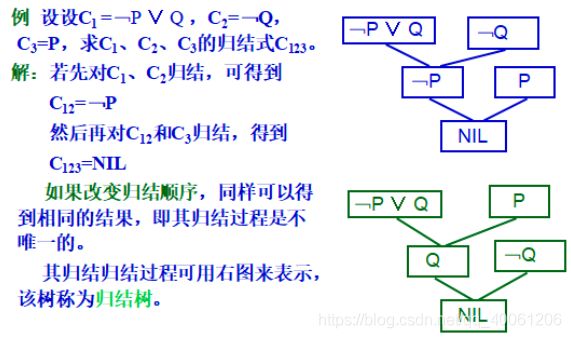
3 归结演绎推理

在人工智能中，几乎所有的问题都可以转化为一个定理证明问题。定理证明的实质，就是要对前提P和结论Q，证明P→Q永真。

但是如何实现对P→Q永真的证明？

1）证明P→Q在任何一个非空域上都是永真的。但是这是很困难的。

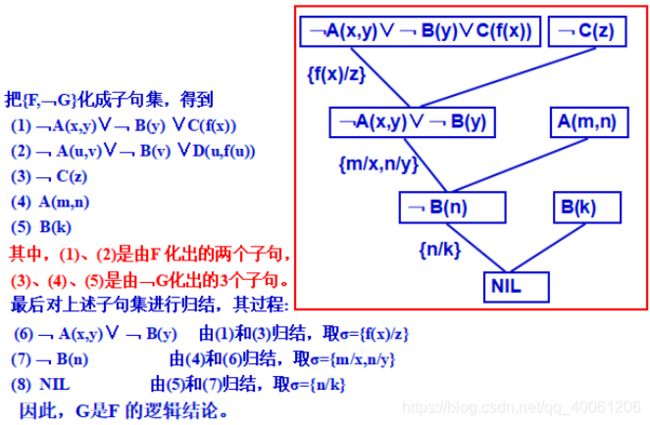
2）根据推理规则， ﹁ (P→Q) ⇔ ﹁(﹁ P∨ Q) ⇔ P∧ ﹁ Q。也就是说，要证明P→Q永真，就是要证明P∧ ﹁Q永假。这样做有什么好处呢？对于P∧ ﹁ Q，将其化为多个为合取关系的子句，只要在这些子句中有一个子句不可满足，则P∧ ﹁ Q不可满足。

定义1：原子谓词公式及其否定统称为文字。如，P(x)、Q(x)、﹁ P(x)、 ﹁ Q(x)等都是文字。

定义2：任何文字的析取式称为子句。如，P(x)∨ Q(x)，P(x，f(x))∨ Q(x，g(x))都是子句。

定义3：不含任何文字的子句称为空子句。由于空子句不含有任何文字，也就不能被任何解释所满足，因此空子句是永假的，不可满足的。空子句一般被记为□或NIL。

定义4：由子句或空子句所构成的集合称为子句集。

3.1 子句集的化简

在谓词逻辑中，任何一个谓词公式都可以通过应用等价关系及推理规则化成相应的子句集。其化简步骤如下：

（1）消条件
（2）减否定
（3）量词变元一致
（4）化前束
（5）消存在
（6）化skolem合取式
（7）消全称
（8）化子句
（9）换变元

下面是每个步骤的详细过程：

3.11 消条件

目标：消去条件连接词“→”和“↔”

方法：反复使用等价公式：P→Q ⇔ ﹁ P∨ Q，P↔Q ⇔ (P∧ Q)∨ (﹁P∧ ﹁Q)

3.12 减少否定符号的辖域

目标：将每个否定符号“﹁”移到紧靠谓词的位置，使得每个否定符号最多只作用于一个谓词上。

方法：

• 双重否定律：¬ ¬ P ⇔ P。
• 摩根定律：¬ (P∨ Q) ⇔ ¬ P∧ ¬ Q，¬ (P∧ Q) ⇔ ¬ P∨ ¬ Q。
• 量词转换率：¬ (∊ x)P ⇔ (∀ x)( ¬ P)，¬ (∀ x)P ⇔ (∊ x) (¬ P)。

如将： (∀ x)(﹁(∀ y)P(x,y)∨ ﹁ (∀ y)(﹁Q(x,y)∨ R(x,y)))

化为：(∀ x)((∊ y)﹁P(x，y)∨ (∊ y)( Q(x，y) ∧ ﹁R(x，y)))

3.13 量词变元一致

目标：使不同量词约束的变元有不同的名字。

方法：在一个量词的辖域内，把谓词公式中受该量词约束的变元全部用另外一个没有出现过的任意变元代替。

如将： (∀ x)((∊ y)﹁P(x，y)∨ (∊ y)( Q(x，y) ∧ ﹁R(x，y)))

化为：(∀ x)((∊ y)﹁P(x，y)∨ (∊ z)( Q(x，z) ∧ ﹁R(x，z)))

3.14 化为前束范式

目标：把所有量词都移到公式的左边

方法：在移动时不能改变其相对顺序；由于第(3)步已对变元进行了标准化，每个量词都有自己的变元，这就消除了任何由变元引起冲突的可能，因此这种移动是可行的。

如将： (∀ x)((∊ y)﹁P(x，y)∨ (∊ z)( Q(x，z) ∧ ﹁R(x，z)))

化为：(∀ x)(∊ y) (∊ z)(﹁P(x，y)∨ ( Q(x，z) ∧ ﹁R(x，z)))

3.15 消去存在量词

方法： 消去存在量词时，需要区分以下两种情况：

1）若存在量词不出现在全称量词的辖域内（即它的左边没有全称量词），只要用一个新的个体常量替换受该存在量词约束的变元，就可消去该存在量词。

2）若存在量词位于一个或多个全称量词的辖域内，例如 (∀ x₁)…(∀ x_n) (∊ y)P(x₁,x₂,…,x_n, y)，则需要用Skolem函数f(x₁,x₂,…,x_n)替换受该存在量词约束的变元y，然后再消去该存在量词。

如，上步所得公式：(∀ x)(∊ y) (∊ z)(﹁P(x，y)∨ ( Q(x，z) ∧ ﹁R(x，z)))中，存在量词(∊ y)和(∊ z)都位于(∀ x)的辖域内，因此都需要用Skolem函数来替换。

设替换y和z的Skolem函数分别是f(x)和g(x)，则替换后的式子为：(∀ x)(﹁P(x,f(x))∨ (Q(x,g(x))∧ ﹁R(x,g(x))))。

注意：这种替换不影响原谓词公式的永假性。

3.16 化为Skolem合取标准形

目标：将谓词公式化为如下Skolem标准形式：

方法：使用等价关系：P∨ (Q∧ R) ⇔ (P∨ Q)∧ (P∨ R)

如将：(∀ x)(﹁P(x,f(x))∨ (Q(x,g(x))∧ ﹁R(x,g(x))))

化为：(∀ x)((﹁P(x,f(x))∨ Q(x,g(x))∧ (﹁P(x,f(x))∨ ﹁R(x,g(x))))

3.17 消去全称量词

方法：由于母式中的全部变元均受全称量词的约束，并且全称量词的次序已无关紧要，因此可以省掉全称量词。但剩下的母式，仍假设其变元是被全称量词量化的。

如将：(∀ x)((﹁P(x,f(x))∨ Q(x,g(x))∧ (﹁P(x,f(x))∨ ﹁R(x,g(x))))

化为：(﹁P(x,f(x))∨ Q(x,g(x)) ∧ (﹁P(x,f(x))∨ ﹁R(x,g(x)))

3.18 化子句

目标：化为谓词之间相互析取的子句。

方法：在母式中消去所有合取词，把母式用子句集的形式表示出来。

如将：(﹁P(x,f(x))∨ Q(x,g(x)) ∧ (﹁P(x,f(x))∨ ﹁R(x,g(x)))

化为：
子句1）：﹁P(x,f(x))∨ ﹁R(x,g(x))
子句2）：﹁P(x,f(x))∨ Q(x,g(x))

3.19 更换变元名称

目标：对子句集中的某些变量重新命名，使任意两个子句中不出现相同的变量名。

如将：﹁P(x,f(x))∨ Q(x,g(x))与﹁P(x,f(x))∨ ﹁R(x,g(x))

化为：﹁P(x,f(x))∨ Q(x,g(x)) ﹁P(y,f(y))∨ ﹁R(y,g(y))

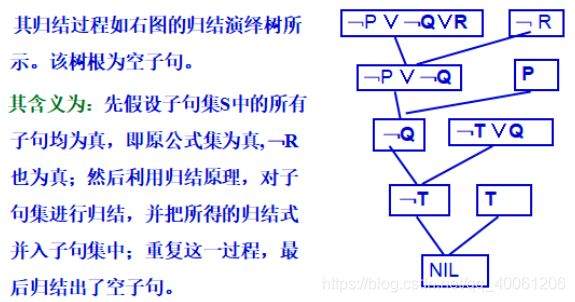
3.2 归结原理

3.2.1 基本思想

3.2.2 命题逻辑的归结

3.2.3 谓词逻辑的归结

---

END