【数学建模笔记 13】数学建模的微分方程建模
13. 微分方程建模
定义
微分方程建模是数学建模的重要方法,大体可以按以下几步:
- 根据实际要求确定要研究的量 (自变量、未知函数、必要参数),确定坐标系;
- 找出这些量所满足的基本规律;
- 运用规律列出方程和定解条件。
微分方程的数值解
考虑一阶常微分方程
{ d y d x = f ( x , y ) , y ( x 0 ) = y 0 . \left\{\begin{aligned} &\frac{dy}{dx}=f(x,y),\\ &y(x_0)=y_0. \end{aligned}\right. ⎩⎨⎧dxdy=f(x,y),y(x0)=y0.
在区间 [ a , b ] [a,b] [a,b] 上的解。
所谓数值解法,就是求 y ( x ) y(x) y(x) 在若干点
a = x 0 < x 1 < x 2 < ⋯ < x N = b a=x_0
处的近似值 y n , n = 1 , 2 , … , N y_n,n=1,2,\dots,N yn,n=1,2,…,N,称
h n = x n + 1 − x n h_n=x_{n+1}-x_n hn=xn+1−xn
为步长,一般取等步长 h = ( b − a ) / N h=(b-a)/N h=(b−a)/N。
为求数值解,首先要将微分方程离散化,方法有:
- 用差商近似导数:
若用向前差商 y ( x n + 1 ) − y ( x n ) h \frac{y(x_{n+1})-y(x_n)}{h} hy(xn+1)−y(xn) 代替 y ′ ( x n ) y'(x_n) y′(xn),代入微分方程,则
y ( x n + 1 ) − y ( x n ) h ≈ f ( x n , y ( x n ) ) , n = 0 , 1 , … , N − 1. \frac{y(x_{n+1})-y(x_n)}{h}\approx f(x_n,y(x_n)),n=0,1,\dots,N-1. hy(xn+1)−y(xn)≈f(xn,y(xn)),n=0,1,…,N−1.
即
y ( x n + 1 ) ≈ y ( x n ) + h f ( x n , y ( x n ) ) . y(x_{n+1})\approx y(x_n)+hf(x_n,y(x_n)). y(xn+1)≈y(xn)+hf(xn,y(xn)).
将 y ( x n ) y(x_n) y(xn) 的近似值 y n y_n yn 代入,即
y n + 1 = y n + h f ( x n , y n ) , n = 0 , 1 , … , N − 1. y_{n+1}=y_n+hf(x_n,y_n),n=0,1,\dots,N-1. yn+1=yn+hf(xn,yn),n=0,1,…,N−1.
于是原方程组化为
{ y n + 1 = y n + h f ( x n , y n ) , n = 0 , 1 , … , N − 1 , y 0 = y ( a ) . \left\{\begin{aligned} &y_{n+1}=y_n+hf(x_n,y_n),n=0,1,\dots,N-1,\\ &y_0=y(a). \end{aligned}\right. {yn+1=yn+hf(xn,yn),n=0,1,…,N−1,y0=y(a).
通过 y 0 y_0 y0 可逐次算出 y 1 , y 2 , … , y N y_1,y_2,\dots,y_N y1,y2,…,yN。
- 数值积分方法:
y ( x n + 1 − y ( x n ) ) = ∫ x n x n + 1 f ( x , y ( x ) ) d x , y(x_{n+1}-y(x_n))=\int_{x_n}^{x_{n+1}}f(x,y(x))dx, y(xn+1−y(xn))=∫xnxn+1f(x,y(x))dx,
右边的积分用矩形或梯形公式计算。
- 泰勒多项式近似:
将 y ( x ) y(x) y(x) 在 x n x_n xn 处展开,即
y ( x n + 1 ) ≈ y ( x n ) + h y ′ ( x n ) y(x_{n+1})\approx y(x_n)+hy'(x_n) y(xn+1)≈y(xn)+hy′(xn)
= y ( x n ) + h f ( x n , y ( x n ) ) , =y(x_n)+hf(x_n,y(x_n)), =y(xn)+hf(xn,y(xn)),
代入近似值得
y n + 1 = y n + h f ( x n , y n ) . y_{n+1}=y_n+hf(x_n,y_n). yn+1=yn+hf(xn,yn).
上式又称欧拉法,为了提高精度,可以使用梯形积分代替矩形积分,称改进欧拉法,即
y n + 1 = y n + h 2 [ f ( x n , y n ) + f ( x n + 1 , y n + 1 ) ] . y_{n+1}=y_n+\frac{h}2[f(x_n,y_n)+f(x_{n+1},y_{n+1})]. yn+1=yn+2h[f(xn,yn)+f(xn+1,yn+1)].
然而由于每一步都会产生截断误差,欧拉法会随着递推误差越来越大。
龙格-库塔法
龙格库塔法的主要思想,就是在 x x x 点附近选取一些特定的点,将这些点的函数值进行线性组合,用组合值代替泰勒展开中的导数值。
根据微分中值定理有
y n + 1 − y ( x n ) h = y ′ ( x n + θ h ) , 0 < θ < 1. \frac{y_{n+1}-y(x_n)}{h}=y'(x_n+\theta h),0<\theta<1. hyn+1−y(xn)=y′(xn+θh),0<θ<1.
又 y ′ = f ( x , y ) y'=f(x,y) y′=f(x,y),于是有
y ( x n + 1 ) = y ( x n ) + h f ( x n + θ h , y ( x n + θ h ) ) . y(x_{n+1})=y(x_n)+hf(x_n+\theta h,y(x_n+\theta h)). y(xn+1)=y(xn)+hf(xn+θh,y(xn+θh)).
记 K ‾ = f ( x n + θ h , y ( x n + θ h ) ) \overline{K}=f(x_n+\theta h,y(x_n+\theta h)) K=f(xn+θh,y(xn+θh)) 为区间 [ x n , x n + 1 ] [x_n,x_{n+1}] [xn,xn+1] 的平均斜率。
欧拉法简单取 K ‾ = f ( x n , y n ) \overline{K}=f(x_n,y_n) K=f(xn,yn),精度很低,而改进欧拉法则取
K ‾ = 1 2 [ f ( x n , y n ) + f ( x n + 1 , y ‾ n + 1 ) ] , \overline{K}=\frac12[f(x_n,y_n)+f(x_{n+1},\overline{y}_{n+1})], K=21[f(xn,yn)+f(xn+1,yn+1)],
y ‾ n + 1 = y n + h f ( x n , y n ) , \overline{y}_{n+1}=y_n+hf(x_n,y_n), yn+1=yn+hf(xn,yn),
则提高了精度。
于是,在区间 [ x n , x n + 1 ] [x_n,x_{n+1}] [xn,xn+1] 内多取几个点进行加权平均作为 K ‾ \overline{K} K,就有可能构造出精度更高的计算公式。
不妨在区间内仍取 2 个点,有
{ y n + 1 = y n + h ( λ 1 k 1 + λ 2 k 2 ) , k 1 = f ( x n , y n ) , k 2 = f ( x n + α h , y n + β h k 1 ) , 0 < α , β < 1. \left\{\begin{aligned} &y_{n+1}=y_n+h(\lambda_1k_1+\lambda_2k_2),\\ &k_1=f(x_n,y_n),\\ &k_2=f(x_n+\alpha h,y_n+\beta hk_1),0<\alpha,\beta<1. \end{aligned}\right. ⎩⎪⎨⎪⎧yn+1=yn+h(λ1k1+λ2k2),k1=f(xn,yn),k2=f(xn+αh,yn+βhk1),0<α,β<1.
又 y n = y ( x n ) y_n=y(x_n) yn=y(xn),则可以化为
{ y n + 1 = y ( x n ) + h ( λ 1 k 1 + λ 2 k 2 ) , k 1 = f ( x n , y ( x n ) ) = y ′ ( x n ) , k 2 = f ( x n + α h , y ( x n ) + β h k 1 ) . \left\{\begin{aligned} &y_{n+1}=y(x_n)+h(\lambda_1k_1+\lambda_2k_2),\\ &k_1=f(x_n,y(x_n))=y'(x_n),\\ &k_2=f(x_n+\alpha h,y(x_n)+\beta hk_1). \end{aligned}\right. ⎩⎪⎨⎪⎧yn+1=y(xn)+h(λ1k1+λ2k2),k1=f(xn,y(xn))=y′(xn),k2=f(xn+αh,y(xn)+βhk1).
k 2 k2 k2 在 ( x n , y ( x n ) ) (x_n,y(x_n)) (xn,y(xn)) 作泰勒展开,则有
k 2 = f ( x n , y ( x n ) ) + α h f x ( x n , y ( x n ) ) k_2=f(x_n,y(x_n))+\alpha hf_x(x_n,y(x_n)) k2=f(xn,y(xn))+αhfx(xn,y(xn))
+ β h k 1 f y ( x n , y ( x n ) ) + O ( h 2 ) . +\beta hk_1f_y(x_n,y(x_n))+O(h^2). +βhk1fy(xn,y(xn))+O(h2).
于是有
y n + 1 = y ( x n ) + ( λ 1 + λ 2 ) h y ′ ( x n ) y_{n+1}=y(x_n)+(\lambda_1+\lambda_2)hy'(x_n) yn+1=y(xn)+(λ1+λ2)hy′(xn)
+ λ 2 α h 2 ( f x + β α f f y ) + O ( h 3 ) . +\lambda_2\alpha h^2(f_x+\frac{\beta}{\alpha}ff_y)+O(h^3). +λ2αh2(fx+αβffy)+O(h3).
可见为使误差 y ( x n + 1 ) − y n + 1 = O ( h 3 ) y(x_{n+1})-y_{n+1}=O(h^3) y(xn+1)−yn+1=O(h3),只须令
λ 1 + λ 2 = 1 , λ 2 α = 1 2 , β α = 1. \lambda_1+\lambda_2=1,\lambda_2\alpha=\frac12,\frac{\beta}{\alpha}=1. λ1+λ2=1,λ2α=21,αβ=1.
解不唯一,其中若
λ 1 = λ 2 = 1 2 , α = β = 1 , \lambda_1=\lambda_2=\frac12,\alpha=\beta=1, λ1=λ2=21,α=β=1,
即为改进欧拉法。
若取 4 个点,就构成常用的四阶龙格-库塔法 RK4
y n + 1 = y n + h 6 ( k 1 + 2 k 2 + 2 k 3 + k 4 ) , y_{n+1}=y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4), yn+1=yn+6h(k1+2k2+2k3+k4),
其中
k 1 = f ( x n , y n ) , k_1=f(x_n,y_n), k1=f(xn,yn),
k 2 = f ( x n + h 2 , y n + h 2 k 1 ) , k_2=f(x_n+\frac{h}{2},y_n+\frac{h}{2}k_1), k2=f(xn+2h,yn+2hk1),
k 3 = g ( x n + h 2 , y n + h 2 k 2 ) , k_3=g(x_n+\frac{h}{2},y_n+\frac{h}{2}k_2), k3=g(xn+2h,yn+2hk2),
k 4 = f ( x n + h , y n + h k 3 ) . k_4=f(x_n+h,y_n+hk_3). k4=f(xn+h,yn+hk3).
k 1 , k 2 , k 3 , k 4 k_1,k_2,k_3,k_4 k1,k2,k3,k4 分别为起点、中点、终点的斜率,通过一定的加权平均使得误差尽可能小。
微分方程建模实例
Malthus 模型
设 x ( t ) x(t) x(t) 表示 t t t 时人口数,人口增长率 r r r 是常数,假设人口数量的变化封闭,即人口数量增加和减少只取决于人口个体的生育和死亡。
则 t t t 时刻到 t + Δ t t+\Delta t t+Δt 时刻,人口增量为
x ( t + Δ t ) − x ( t ) = r x ( t ) Δ t , x(t+\Delta t)-x(t)=rx(t)\Delta t, x(t+Δt)−x(t)=rx(t)Δt,
于是得
{ d x d t = r x , x ( 0 ) = x 0 . \left\{\begin{aligned} &\frac{dx}{dt}=rx,\\ &x(0)=x_0. \end{aligned}\right. ⎩⎨⎧dtdx=rx,x(0)=x0.
解为
x ( t ) = x 0 e r t . x(t)=x_0e^{rt}. x(t)=x0ert.
然而模型的预测结果远高于实际人口增长,误差的原因是对增长率 r r r 估计过高。
Logistic 模型
由于资源是有限的,随着人口数量增长,资源对人口增长的限制将越来越显著。人口较少时可以将增长率 r r r 看作常数,到达一定数量后 r r r 应随人口增加而减小。因此,将 r r r 表示为人口 x ( t ) x(t) x(t) 的函数 r ( x ) r(x) r(x),且 r ( x ) r(x) r(x) 为 x x x 的减函数。
设 r ( x ) r(x) r(x) 为 x x x 的线性函数, r ( x ) = r − s x r(x)=r-sx r(x)=r−sx。
设容纳最大人口为 x m x_m xm,当 x = x m x=x_m x=xm 时, r ( x m ) = 0 r(x_m)=0 r(xm)=0。
于是有
r ( x ) = r ( 1 − x x m ) , r(x)=r(1-\frac{x}{x_m}), r(x)=r(1−xmx),
得
{ d x d t = r ( 1 − x x m ) x , x ( t 0 ) = x 0 . \left\{\begin{aligned} &\frac{dx}{dt}=r(1-\frac{x}{x_m})x,\\ &x(t_0)=x_0. \end{aligned}\right. ⎩⎪⎨⎪⎧dtdx=r(1−xmx)x,x(t0)=x0.
解为
x ( t ) = x m 1 + ( x m x 0 − 1 ) e − r ( t − t 0 ) . x(t)=\frac{x_m}{1+(\frac{x_m}{x_0}-1)e^{-r(t-t_0)}}. x(t)=1+(x0xm−1)e−r(t−t0)xm.
以 r , x m r,x_m r,xm 为变量,对某一数据集进行拟合,就可以得到结果。
Python 代码
微分方程求解
求微分方程
{ y ′ = − 2 y + x 2 + 2 x , y ( 1 ) = 2. \left\{\begin{aligned} &y'=-2y+x^2+2x,\\ &y(1)=2. \end{aligned}\right. {y′=−2y+x2+2x,y(1)=2.
的解析解和数值解,代码如下:
#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date: 2021-7-27
# @ function: 使用 scipy、sympy 求微分方程的数值解、解析解
# %%
import numpy as np
from scipy.integrate import odeint
from sympy import *
# %%
# 使用 scipy 求数值解
# 微分方程
dy = lambda y,x:-2*y + x**2 + 2*x
# 数值范围
x1 = np.linspace(1,10,20)
# 求数值解,y 的初始值为 2
y1 = odeint(dy, 2, x1)
y1
# %%
# 使用 sympy 求解析解
# 定义变量和函数
x = symbols('x', real=True)
y = Function('y')
# 定义方程和约束
eq = y(x).diff(x) + 2*y(x) - x**2 - 2*x
con = {
y(1): 2,
}
# 求解
f = simplify(dsolve(eq, ics=con))
f
# %%
# 向解中代入不同的值
x2 = np.linspace(1,10,100)
y2 = []
for each in x2:
y2.append(list(sorted(f.subs(x,each).evalf().atoms()))[1])
# %%
# 画图
import matplotlib.pyplot as plt
plt.scatter(x1,y1, label='x1', color='coral')
plt.plot(x2,y2, label='x2')
plt.legend()
输出如下:
y ( x ) = x 2 2 + x 2 + 5 e 2 − 2 x 4 − 1 4 y(x)=\frac{x^2}{2}+\frac{x}{2}+\frac{5e^{2-2x}}{4}-\frac14 y(x)=2x2+2x+45e2−2x−41
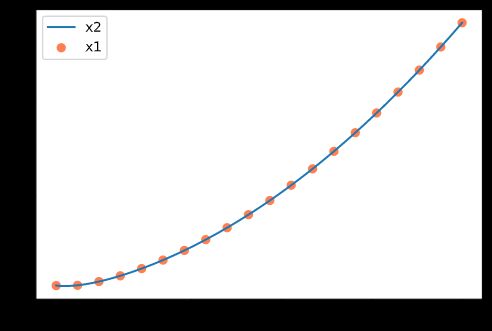
得到解析解的公式,以及数值解 x 1 x_1 x1 和解析解的曲线 x 2 x_2 x2,发现数值解和解析解大致吻合。
Logistic 模型
对下列人口数据:
| 年份 | 人口 |
|---|---|
| 1790 | 3.9 |
| 1800 | 5.3 |
| 1810 | 7.2 |
| 1820 | 9.6 |
| 1830 | 12.9 |
| 1840 | 17.1 |
| 1850 | 23.2 |
| 1860 | 31.4 |
| 1870 | 38.6 |
使用 Logistic 模型拟合,求出 r , x m r,x_m r,xm 的值。
代码如下:
#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date: 2021-7-27
# @ function: 使用 Logistic 模型拟合人口数据
# %%
import numpy as np
import pandas as pd
from scipy.optimize import curve_fit
# %%
# 源数据
df = pd.DataFrame({
'year': [1790, 1800, 1810, 1820, 1830, 1840, 1850, 1860, 1870],
'population': [3.9, 5.3, 7.2, 9.6, 12.9, 17.1, 23.2, 31.4, 38.6],
})
x0 = float(df['population'][0])
t0 = float(df['year'][0])
# %%
# Logistic 模型
def x(t, r, xm):
return xm / (1 + (xm/x0-1)*np.exp(-r*(t-t0)))
# 拟合参数
popt, pcov = curve_fit(x,
df['year'].tolist(),
df['population'].tolist(),
bounds=((0, 1), (.1, np.inf)))
r, xm = popt[0], popt[1]
print('r =', r)
print('xm =', xm)
# 预测 1900 人口
print('population in 1900 =', x(1900, r, xm))
# %%
# 画出预测曲线
import matplotlib.pyplot as plt
year = np.linspace(1790,2000,21)
population = []
for each in year:
population.append(x(each,r,xm))
plt.scatter(df['year'], df['population'], label='actual')
plt.plot(year, population, label='predict', color='coral')
plt.legend()
输出如下:
r = 0.031999710099329476
xm = 159.3028433863908
population in 1900 = 73.09203839061287

得到 r = 0.032 , x m = 159.3 r=0.032,x_m=159.3 r=0.032,xm=159.3,并预测 1900 年人口为 73.09 73.09 73.09,得到预测曲线。