sklearn的系统学习——随机森林分类器与随机森林回归器(含有python完整代码及案例)
目录
集成算法
sklearn中的随机森林
随机森林分类器
随机性参数
属性
案例代码
随机森林回归器
案例代码
在前面的内容中,已经对决策树解决分类回归问题分别做了阐述,今天走进随机森林的世界。
什么是森林呢,对,好多树在一起我们就叫它森林,为什么是随机呢,因为这片森林可能不一样,这就涉及到参数的设定了(就像之前决策树的参数一样)。
名字的意义明白了,那这最终的结果是怎么得出来的呢?其实很简单,我们知道一棵决策树会给出一个结果,多棵树就会给出多个结果,最后”投票“表决,得票高的就是最终随机森林给出的结果喽。(当然,这里的解释较为简单,想知道具体原理可以阅读《数据挖掘导论》和西瓜书。)
集成算法
集成学习算法本身不算一种单独的机器学习算法,而是通过构建并结合多个机器学习器来完成学习任务。
目标:集成算法会考虑多个评估器的建模结果,汇总之后得到一个综合的结果,以此获取比单个模型更好的回归或者分类效果。
集成评估器:多个模型集成后的模型,如随机森林。
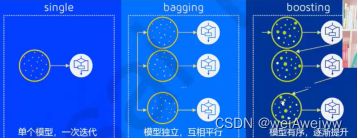
分类:bagging(袋装法),boosting(提升法),stacking。主要介绍前两个。
bagging(袋装法):模型之间相互独立,互相平行,如随机森林。
boosting(提升法):模型之间不相互独立,且模型有序,逐渐提升,如adaboost。
sklearn中的随机森林
随机森林分类器
参数列表几乎与决策树的相同,重要的有:
criterion, max_depth, min_samples_leaf, min_samples_split, max_features, min_impurity_decrease
n_estimators树木的数量,越大往往越好,但达到一定程度之后精确性往往会上下波动,默认10,0.22版本会改为100,一般0-200选一个比较好。
.除此之外,还需要注意的是关于随机性的这两个参数:
随机性参数
1、random_state
当random_state固定时,随机森林中生成的是一组固定的树,但每棵树依然不一致,这是随机挑选特征进行分枝的方法。当随机性越大的时候,袋装法的效果一般会越来越好,用袋装法集成时,基分类器应该是相互独立,是不相同的。
但是局限性强,数据可能没有足够多的特征构建成千上万棵不同的树,因此还需要其他方式。
2、bootstrap & oob_score
使用不同的训练集,袋装法有放回随机抽样技术来形成不同的训练数据,bootstrap就是控制抽样技术的参数。
但是这又会引出如下问题:一些样本可能在同一个自助集出现多次,而其他一些却可能被忽略。一般来说,自助集大约包含63%的原始数据,计算方式:1-(1-1/n)**n,这里是按逆向思维进行计算的:每次都不被选中,总共进行n次,总概率1减去该值即为如上结果。
那既然大约63%的数据被使用,就会有约37%的数据未被使用,这个数据集叫做袋外数据(out of bag data,oob)。除开始划分的测试集,这些也可以用来当测试集——所以,在使用随机森林时,可以不划分测试集和训练集,只需要袋外数据来测试我们的模型即可,当然也不绝对,因为当n和n_estimators都不够大时,很可能就没有数据掉到袋外,自然也就无法使用oob数据来测试模型。
属性
相较决策树,随机森林除feature_importances属性外,
#重要性
importance = clf.feature_importances_
feature_importance = [(feature,importance.round(3)) for feature,importance in zip(feature_name,importance)]
#排序
feature_importance = sorted(feature_importance,key=lambda x :x[1],reverse=True)
#对应进行打印
[print('variable:{:20} importance: {}'.format(*pair)) for pair in feature_importance]还有如下两个属性:
1、estimators_
#随机森林的重要属性:estimators_,查看森林中树的情况
print(rf.estimators_)
rf.estimators_[1].random_state2、 oob_score
rf = RandomForestClassifier(n_estimators=25,random_state=42,oob_score=True)
oob = rf.oob_score_案例代码
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
wine = load_wine() #字典
print(wine.data) #可以通过键取值
print(wine.data.shape)
print(wine.target)
xtrain,xtest,ytrain,ytest = train_test_split(wine.data,wine.target,test_size=0.3)
rf = RandomForestClassifier(n_estimators=25,random_state=42,oob_score=True)
clf = DecisionTreeClassifier(random_state=42)
#交叉验证
cross_rf = cross_val_score(rf,wine.data,wine.target,cv=5)
cross_clf = cross_val_score(clf,wine.data,wine.target,cv=5)
rf.fit(xtrain,ytrain)
score_rf = rf.score(xtest,ytest)
oob = rf.oob_score_
clf.fit(xtrain,ytrain)
score_clf = clf.score(xtest,ytest)
print('===',score_clf.round(3),score_rf.round(3),oob.round(3))
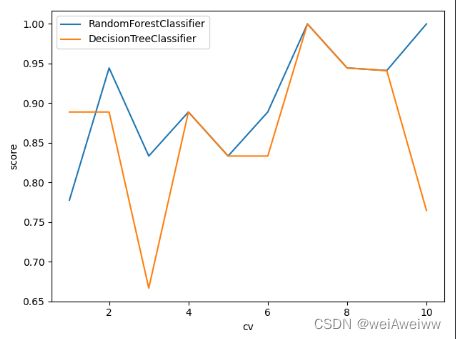
plt.plot(range(1,6),cross_clf,label='DecisionTreeClassifier')
plt.plot(range(1,6),cross_rf,label='RandomForestClassifier')
plt.xlabel('cv')
plt.ylabel('score')
plt.legend()
plt.show()
#随机森林的重要属性:estimators_,查看森林中树的情况
print(rf.estimators_)
for i in range(len(rf.estimators_)):
print(rf.estimators_[i].random_state)
################换一种写法##############
cv = 10
for model in [RandomForestClassifier(n_estimators=5,random_state=42),DecisionTreeClassifier(random_state=42)]:
cross = cross_val_score(model, wine.data, wine.target, cv=cv)
plt.plot(range(1,cv+1),cross,label='{}'.format(str(model).split('(')[0]))
plt.xlabel('cv')
plt.ylabel('score')
plt.legend()
plt.show()
##################学习曲线################
# superpa = []
# for i in range(200):
# rf = RandomForestClassifier(random_state=42,n_estimators=i+1)
# sc = cross_val_score(rf,wine.data,wine.target,cv=10).mean()
# superpa.append(sc)
# plt.plot(range(1,201),superpa)
# print(max(superpa),superpa.index((max(superpa))))
# plt.show()
import numpy as np
from scipy.special import comb
# 建立25棵树,当且仅当有13棵以上的树判断错误时,随机森林才会报错
# 如果一棵树的准确率在0.85上下浮动,那20棵树以上判断错误的概率
sum = np.array([comb(25,i)*(0.2**i)*((1-0.2)**(25-i)) for i in range(13,26)]).sum()
print(sum)
随机森林回归器
这里其实不用再多做介绍,与决策树回归一致,请回看这里。https://blog.csdn.net/weixin_44904136/article/details/126201929![]() https://blog.csdn.net/weixin_44904136/article/details/126201929不过,值得一说的是它的应用,我们可以通过随机森林回归器填补缺失值。
https://blog.csdn.net/weixin_44904136/article/details/126201929不过,值得一说的是它的应用,我们可以通过随机森林回归器填补缺失值。
测试集与训练集的划分思想:
xtrain:特征不缺失的值对应其他的n-1个特征 + 本来的标签
ytrain:特征不缺失的值
xtest:特征缺失的值对应其他的n-1个特征 + 本来的标签
ytest:特征缺失的值
适用于某一个特征大量缺失,而其他特征相对完整。
对,相对完整,也就是其他特征也可能存在缺失,那该怎么办呢?
答:我们首先通过检查特征空值,转化为布尔值加和(比较直观,0说明空,非0说明非空),进行排序,目的是先计算特征缺失少的部分,然后循环遍历。
选定特征之后,将其他特征的缺失值赋为0(这里注意复制原矩阵到新矩阵,避免原矩阵被补0覆盖),之后就是回归问题了。
案例代码
from sklearn.ensemble import RandomForestRegressor
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_boston
import pandas as pd
from sklearn.impute import SimpleImputer #填补缺失值
#评估指标
import sklearn
# print(sklearn.metrics.SCORERS.keys())
# sklearn.impute.SimpleImputer
boston = load_boston()
# print(boston.data.shape) #(506, 13)
# print(boston.target)
#####################将数据集改为有缺失的数据集(特征为空)#####################
x_full,y_full = boston.data,boston.target
n_samples = x_full.shape[0]
n_features = x_full.shape[1]
rng = np.random.RandomState(0)
missing_rate = 0.5
n_missing_samples = int(np.floor(n_samples * n_features * missing_rate)) #np.floor向下取整
#所有数据要随机遍布在数据集的各行各列当中,而一个缺失的数据会需要一个行索引和一个列索引
# 如果能创造一个数组,包含3289个分布在0-506中间的行索引,和3289个分布在0-13之间的列索引
# 那我们就可以利用索引来为数据中的任意3289个位置赋空值
# 然后我们用0,均值和随机森林来填写这些缺失值,然后查看回归的结果
miss_features = rng.randint(0,n_features,n_missing_samples)
# randint(下限,上限,n) 请在下限和上限之间取出n个整数
miss_samples = rng.randint(0,n_samples,n_missing_samples)
# rng.choice(n_samples,n_missing_samples,replace=False) 抽取不重复的随机数
x_missing= x_full.copy()
y_missing = y_full.copy()
x_missing[miss_samples,miss_features] = np.nan
x_missing = pd.DataFrame(x_missing)
print(x_missing)
print('==============')
####################填补缺失值############################
####使用均值进行填补
imp_mean = SimpleImputer(missing_values=np.nan,strategy='mean') #实例化
x_missing_mean = imp_mean.fit_transform(x_missing) #训练加导出
####使用0进行填补
imp_0 = SimpleImputer(missing_values=np.nan,strategy='constant',fill_value=0)
x_missing_0 = imp_0.fit_transform(x_missing)
#查看是否填补完毕
a = pd.DataFrame(x_missing_mean).isnull().sum()
b = pd.DataFrame(x_missing_0).isnull().sum()
# print(a)
# print(b)
####使用随机森林去填写缺失值
x_missing_reg = x_missing.copy()
#找出特征集中,缺失值从小到大排列的特征顺序(找索引)
sortindex = np.argsort(x_missing_reg.isnull().sum(axis=0)).values #有索引 而sort()无索引
for i in sortindex:
#构建新矩阵,防止下一步补0操作将原矩阵覆盖
df = x_missing_reg
fillc = df.iloc[:,i]
df = pd.concat([df.iloc[:,df.columns != i],pd.DataFrame(y_full)],axis=1)
#在新特征矩阵中,对缺失列补0,
df_0 = SimpleImputer(missing_values=np.nan,strategy='constant',fill_value=0).fit_transform(df)
#划分训练集和测试集
ytrain = fillc[fillc.notnull()] #被选中特征中存在值的行
ytest = fillc[fillc.isnull()] #被选中特征中空值的行
xtrain = df_0[ytrain.index,:]
xtest = df_0[ytest.index,:]
#用随机森林预测特征
rf = RandomForestRegressor(n_estimators=100,random_state=42)
rf.fit(xtrain,ytrain)
prediction = rf.predict(xtest)
#将预测出的特征值填入缺失列中
x_missing_reg.loc[x_missing_reg.iloc[:,i].isnull(),i] = prediction
print(pd.DataFrame(df))
print(x_missing_reg.isnull().sum()) #是否为空:是1 不是0,最后结果都为0,所以此时矩阵无空处,填补完成
#################对填充好的数据进行模型训练###################
x = [x_full,x_missing_mean,x_missing_0,x_missing_reg]
mse = []
for i in x:
estimator = RandomForestRegressor(n_estimators=100,random_state=42)
estimator.fit(i,y_full)
scores = cross_val_score(estimator,i,y_full,scoring='neg_mean_squared_error',cv = 5).mean()
mse.append(scores * -1)
# print(mse) #mse越小越好
print([*zip(['x_full','x_missing_mean','x_missing_0','x_missing_reg'],mse)])
#################绘图################################
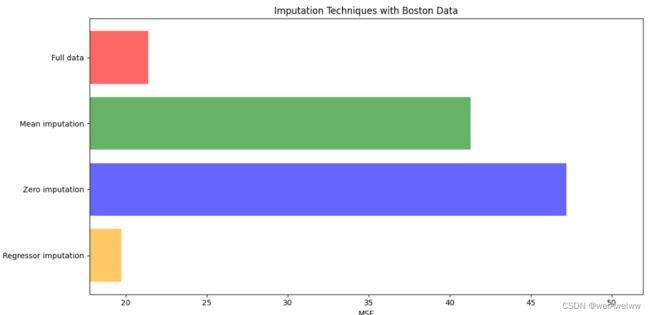
x_labels = ['Full data','Mean imputation','Zero imputation','Regressor imputation']
colors = ['r','g','b','orange']
plt.figure(figsize=(12,6)) #画出画布
ax = plt.subplot(111) #添加子图
for i in np.arange(len(mse)):
ax.barh(i,mse[i],color=colors[i],alpha=0.6,align='center') #横向条形图
ax.set_title('Imputation Techniques with Boston Data')
ax.set_xlim(left=np.min(mse)*0.9,
right=np.max(mse)*1.1) #刻度
ax.set_yticks(np.arange(len(mse)))
ax.set_xlabel('MSE') #x轴名字
ax.invert_yaxis()
ax.set_yticklabels(x_labels)
plt.show()
随机森林的介绍就到此结束喽,但是对于性能的提升问题,也就是调参问题,我们下一篇来接着说~