每天进步一点点 -- pytorch学习：MNIST手写数字初体验

理论计算方法 -- K临近算法(OpenCV轻松入门_面向python)

        K 近邻算法的本质是将指定对象根据已知特征值分类，根据书中给出的内容，我们可以在手写数字识别上进行分析。
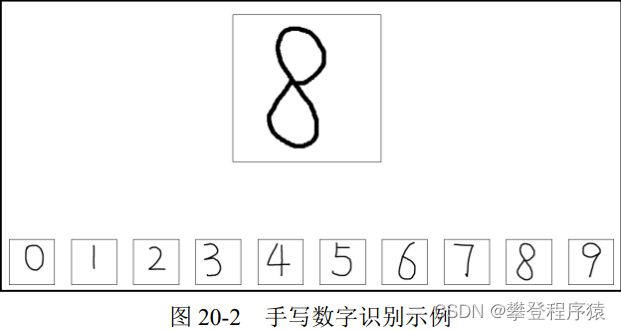
        假设我们要让程序识别图20-2中上方的数字（当然，你一眼就知道是“8”，但是现在要让计算机识别出来）。识别的方式是，依次计算该数字图像（即写有数字的图像）与下方数字图像的距离，与哪个数字图像的距离最近（此时k=1），就认为它与哪幅图像最像，从而确定这幅图像中的数字是多少。
  从特征值提取和数字识别两方面展开介绍：
 

 特征值提取

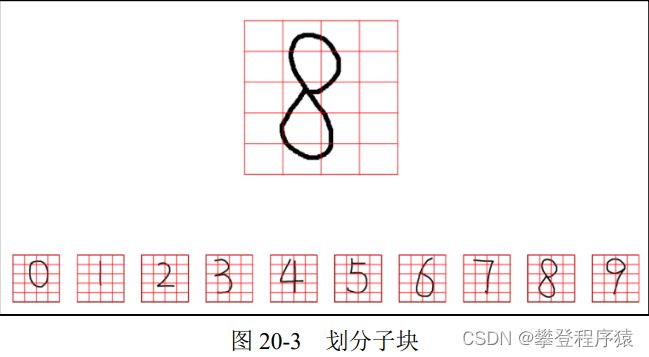
        步骤1：我们把数字图像划分成很多小块，如图20-3所示。该图中每个数字被分成5行4列，共计5×4=20个小块。此时，每个小块是由很多个像素点构成的。当然，也可以将每一个像素点理解为一个更小的子块。
        为了叙述上的方便，将这些小块表示为B（Bigger），将B内的像素点，记为S（Smaller）。因此，待识别的数字“8”的图像可以理解为：
        ● 由5行4列，共计5×4=20个小块B构成。
        ● 每个小块B内其实是由M×N个像素（更小块S）构成的。为了描述上的方便，假设每个小块大小为10×10=100个像素。

         步骤2：计算每个小块B内，有多少个黑色的像素点。或者这样说，计算每个小块B内有多少个更小块S是黑色的。
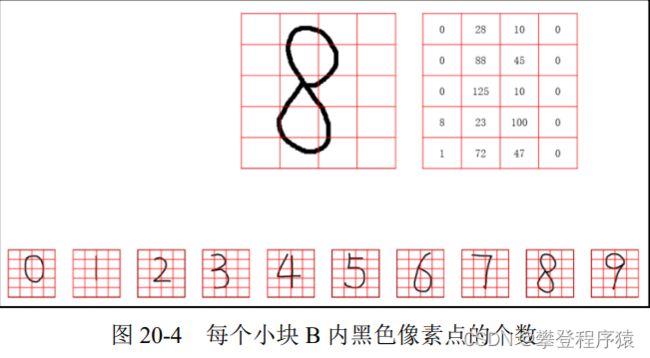
        仍以数字“8”的图像为例，其第1行中：
        ● 第1个小块B共有0个像素点（更小块S）是黑色的，记为0。
        ● 第2个小块B共有28个像素点（更小块S）是黑色的，记为28。
        ● 第3个小块B共有10个像素点（更小块S）是黑色的，记为10。
        ● 第4个小块B共有0个像素点（更小块S）是黑色的，记为0。
以此类推，计算出数字“8”的图像中每一个小块B中有多少个像素点是黑色的，如图20-4所示。我们观察后会发现，不同的数字图像中每个小块B内黑色像素点的数量是不一样的。正是这种不同，使我们能用该数量（每个小块B内黑色像素点的个数）作为特征来表示每一个数字。

        步骤3：有时，为了处理上的方便，我们会把得到的特征值排成一行（写为数组形式），如图20-5所示。

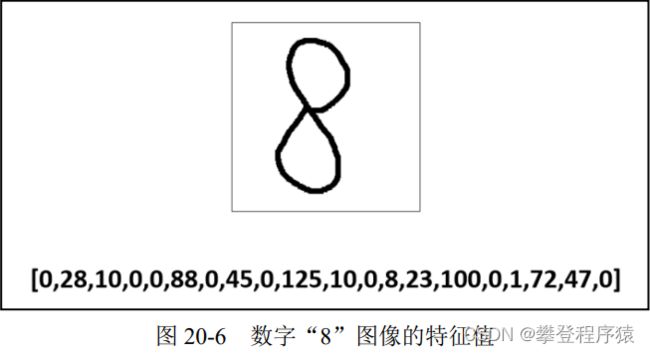
         当然，在 Python 里完全没有必要这样做，因为 Python 可以非常方便地直接处理图 20-5 中 上方数组（array）形式的数据。这里为了说明上的方便，仍将其特征值处理为一行数字的形式。 经过上述处理，数字“8”图像的特征值变为一行数字，如图 20-6 所示

        步骤4：与数字“8”的图像类似，每个数字图像的特征值都可以用一行数字来表示。从某 种意义上来说，这一行数字类似于我们的身份证号码，一般来说，具有唯一性。 按照同样的方式，获取每个数字图像的特征值，如图 20-7 所示。 

 

数字识别

        数字识别要做的就是比较待识别图像与图像集中的哪个图像最近。这里，最近指的是二者 之间的欧氏距离最短。

        本例中为了便于说明和理解进行了简化，将原来下方的 10 个数字减少为 2 个（也即将分 类从 10 个减少为 2 个）。假设要识别的图像为图 20-8 中上方的数字“8”图像，需要判断该图 像到底属于图 20-8 中下方的数字“8” 图像的分类还是数字“7”图像的分类。

         步骤1：提取特征值，分别提取待识别图像的特征值和特征图像的特征值。
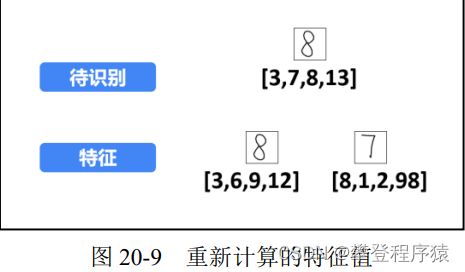
        为了说明和理解上的方便，将特征进行简化，每个数字图像只提取4个特征值（划分为2× 2=4个子块B），如图20-9所示。此时，提取到的特征值分别为：   

        步骤2：计算距离。 按照 20.1 节介绍的欧氏距离计算方法，计算待识别图像与特征图像之 间的距离。

        步骤3：识别。

         根据计算的距离，待识别的数字“8”图像与数字“8”特征图像的距离更近。所以，将待 识别的数字“8”图像识别为数字“8”特征图像所代表的数字“8”。

        上面介绍的是 K 近邻算法只考虑最近的一个邻居的情况，相当于 K 近邻中 k =1 的情况。 在实际操作中，为了提高可靠性，需要选用大量的特征值。例如，每个数字都选用不同的形态 的手写体 100 个，对于 0 ~ 9 这 10 个数字，共需要 100×10 =1000 幅特征图像。在识别数字时， 分别计算待识别的数字图像与这些特征图像之间的距离。这时，可以将 k 调整为稍大的值，例 如 k =11，然后看看其最近的 11 个邻居分属于哪些特征图像。例如，其中：

•  有 8 个属于数字“6”特征图像。
•  有 2 个属于数字“8”特征图像。
•  有 1 个属于数字“9”特征图像。

通过判断，当前待识别的数字为数字“6”特征图像所代表的数字“6”

Pytorch实战  -- 神经网络

        上面的方法已经证明了，将图像一维化之后，仍然可以作为特征找到属于哪个数字，那么，Pytorch实战的理论部分就很容易理解了，课程使用的是神经网络，不是用的K临近。

数据集获取

        数据集使用的是标准MNIST数据集，相关介绍可以看官网，也可以随意百度，简单来说就是一个X矩阵，一个Y矩阵，X矩阵的一行代表一个28*28的图片矩阵按行打平之后的一行784列的矩阵，Y就是上面X对应的数字。

模型选择

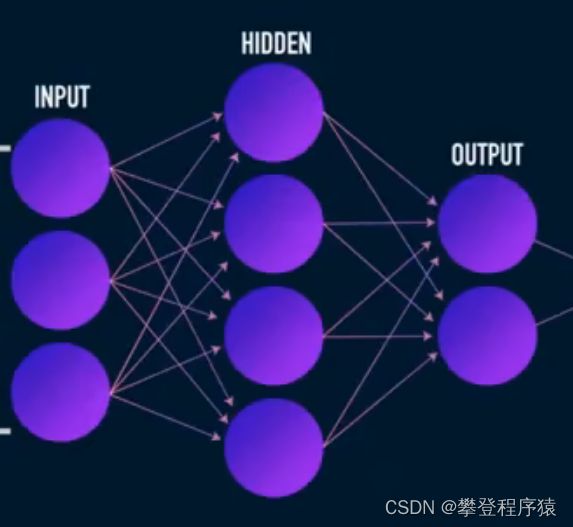
        既然课程使用的神经网络，自己对神经网络也不是很懂，那就参考课程理一下思路，构建的是三层神经网络，输入为X，则为一行784列的行向量，网络输入需要784维，中间层输入参考课程使用64维，outPut需要按照数字对比，参考上面K临近时的输出，为one_shot的结果，0-9共10个数，即需要输出10维，激活函数前两层选择ReLU(容易求导)，输出层的激活函数选择线性，1

此方法使用三层神经网络来做，三层网络如下：  

注：如果听原课程，一定要注意X:[1,dx]代表了X为1行784列的行向量，依次类推

代码实现

"""
 @Author: Administrator
 @DateTime: 2022/12/10 20:16
 Copyright (c) 2022-2025 zhaofeiTec
"""
# !/usr/bin/python
# coding: utf-8

import torch
import torch.nn as nn  # 网络模型
import torch.nn.functional as F  # 方法
from torch import optim
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
# 数据批处理的的图片个数
from utils import one_hot, plot_curve

BATCH_SIZE = 64
# 使用训练的设备
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# 训练的总轮次
EPOCHS = 1

# 构建transform,对图像进行变换
pipeline = transforms.Compose([
    transforms.ToTensor(),  # 将图片转换成tensor形式
    transforms.Normalize((0.1307,), (0.3081,))  # 参数使用的官网的，需要自己设定，模型出现过拟合现象时，降低模型复杂度
])

# 下载数据集
train_set = datasets.MNIST("data", train=True, download=True, transform=pipeline)  # 下载现有的数据集，保存到data
test_set = datasets.MNIST("data", train=False, download=True, transform=pipeline)  # 下载测试数据集
train_loader = DataLoader(train_set, batch_size=BATCH_SIZE, shuffle=True)  #
test_loader = DataLoader(test_set, batch_size=BATCH_SIZE, shuffle=False)


class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()

        # xW+b
        self.fc1 = nn.Linear(28 * 28, 256)  # 784维的输入，输出256维
        self.fc2 = nn.Linear(256, 64)  # 256维的输入，64维的输出
        self.fc3 = nn.Linear(64, 10)  # 64维的输入，10维的输出

    def forward(self, x):
        # x为1行784列的矩阵
        # h1 = relu(xW1 +b)
        x = F.relu(self.fc1(x))
        # h2 = relu(h1W2 +b)
        x = F.relu(self.fc2(x))
        # 先不加激活函数
        # h3 = h2W3+b
        x = self.fc3(x)
        return x


net = Net()
# net.parameters() 为net的优化对象，w1,b1,w2,b2,w3,b3 lr为学习率，momentum暂时未知
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)

train_loss = []
# 循环所有训练集3次
for epoch in range(3):
    for batch_idx, (x, y) in enumerate(train_loader):
        # x [64,1,28,28] 64个图片， y 为64行
        # 打平后 x [64,748] 64行748列
        x = x.view(x.size(0), 28 * 28)
        out = net(x)
        y_one_hot = one_hot(y)
        # loss mse为方差
        loss = F.mse_loss(out, y_one_hot)
        # 优化器
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        # 保存训练集的损失函数
        train_loss.append(loss.item())

plot_curve(train_loss)

util.py:

"""
 @Author: Administrator
 @DateTime: 2022/12/10 23:19
 Copyright (c) 2022-2025 zhaofeiTec
"""
import matplotlib.pyplot as plt
# !/usr/bin/python
# coding: utf-8
import torch


def plot_curve(data):
    fig = plt.figure()
    plt.plot(range(len(data)), data, color="blue")
    plt.legend(['value'], loc='upper right')
    plt.xlabel('step')
    plt.ylabel('value')
    plt.show()


def plot_image(img, label, name):
    fig = plt.figure()
    for i in range(6):
        plt.subplot(2, 3, i + 1)
        plt.tight_layout()
        plt.imshow(img[0] * 0.3081 + 0.1307, cmap='gray', interpolation='none')
        plt.title("{}:{}".format(name, label[i].item()))
        plt.xticks()
        plt.yticks()
    plt.show()


def one_hot(labels, depth=10):
    out = torch.zeros(labels.size(0), depth)
    idx = torch.LongTensor(labels).view(-1, 1)
    out.scatter_(dim=1, index=idx, value=1)
    return out

测试集验证和模型泛化性能分析

此处缺失

仅保存损失函数随训练过程的下降 

问题解决

（1）pytorch是使用Anaconda安装的python环境，使用Anaconda无法安装matplotlib，解决方法如下：

进去Anaconda的安装目录下pytorch环境的安装路径：D:\software\Anaconda3\envs\pytorch\Scripts，右击，本地打开PowerShell,执行下面的命令即可：

 .\pip.exe install matplotlib -i http://pypi.douban.com/simple --trusted-host pypi.douban.com

重启Pycharm后，已经可以使用matplotlib