CVPR 2022 Oral 学习不分割的内容：关于小样本分割的新视角

论文题目：Learning What Not to Segment: A New Perspective on Few-Shot Segmentation

论文地址：https://arxiv.org/pdf/2203.07615.pdf

开源代码：https://github.com/chunbolang/BAM

近年来，小样本分割（Few-shot Segmentation, FSS） 得到了广泛的发展。以往的大多数工作都力求通过分类任务衍生出的元学习框架来实现泛化；然而，训练的模型偏重于所看到的类，而不是理想的类不可知论，从而阻碍了新概念的识别。本文提出了一个全新且直接的视角来缓解这一问题。具体地说，该文在传统的FSS模型（元学习器，即meta learner）上增加了一个分支（基学习器，即base learner）来显式地识别基类的目标，即不需要分割的区域。然后，对这两个学习器并行输出的粗结果进行自适应集成，以产生精确的分割预测。考虑到元学习器的敏感性，我们进一步引入了一个调整因子来估计输入图像对之间的场景差异，以促进模型集成预测。此外，鉴于所提方法的独特性，该文还将其推广到一个更现实但更具挑战性的场景，即广义FSS，即基类和新类都需要预测的任务。

01、引言

众所周知，人类可以很容易地从少数几个例子中识别出新的概念或模式。基于此，人们建立起小样本学习（Few-shot Learning, FSL） 的方法，它通过建立一个网络来用稀少的注释样本推广到未知的领域。小样本分割是小样本学习技术在密集预测任务中的自然应用，近年来受到越来越多的关注。以前的方法通常采用双分支结构：支持分支（Support branch）和查询分支（Query branch），来传递标注信息，并在提取的特征之间进行交互。然而，在具有大量标注样本的基数据集上进行元训练不可避免地引入了对已见类的偏见，而不是理想的类不可知论（class-agnostic），从而阻碍了对新类的识别。

对此，本文给出的解决方案是，在传统的FSS模型中引入了一个额外的分支来显式地预测基类的目标，这个额外分支被称为基学习器（图1）。本文中提出的模型被命名为BAM（Base and the Meta）。本文在元学习器中引入了基于扩张卷积的atrous空间金字塔池（ASPP） 模块^[1]，以扩大元学习器的接收域，并以PSPNet^[2]为基础学习器，预测基础类别中的干扰对象。

图1：本文提出的BAM与之前工作的比较。(a) 传统方法通常使用元学习框架来训练FSS模型，这不可避免地偏向于基类，而不是理想的类不可知论，因此阻碍了对新类的目标对象的识别。（b）我们的BAM引入了一个额外的分支，即基学习器，以显式地预测基类的区域。这样，在集成模块之后，可以显著地抑制查询图像中的分心对象。（c）在广义FSS设置下扩展了我们的BAM模型，其中需要确定基类和新类的像素。改进的结果再次与基学习器的输出合并，以生成综合预测。

受在图像风格迁移领域广泛采用的风格损失（style loss） 的启发，我们首先计算两幅输入图像的Gram矩阵之差，然后利用 Frobenius 范数得到指导调整过程的总体指标。

总之，本文的主要贡献可归纳如下：

• 提出了一种简单而有效的方法，通过引入一个额外的分支来显式地预测查询图像（Query image） 中基类的区域，从而解决了偏差问题，为以后的工作提供了指导。
• 提出通过 Gram 矩阵估计 Support-Query 图像对之间的场景差异，以减轻元学习器敏感性带来的不利影响。
• 即便使用了两个普通的学习器，本文提出的方法也在小样本分割领域中取得了 SOTA 的性能。
• 我们将所提出的方法扩展到一个更具挑战性的设置，即广义 FSS，它同时识别基类和新类的目标。

02、方法

为了解决现有 FSS 方法存在的偏差问题，本文提出建立一个额外的网络来显式预测查询图像中基类的区域，从而方便新对象的分割。在不失通用性的前提下，我们在 One-Shot 设置下给出了我们的模型的整体架构，如图2所示。

图2：BAM的总体结构，它由三个基本组成部分组成：基学习器，元学习器和集成模块。

BAM 由三个主要部分组成，包括两个互补学习者（即基学习器和元学习器）和一个集成模块。两个学习器共享网络主干，分别用于识别基类和新类。然后，集成模块接收它们的粗预测和一个调整因子来抑制基类的错误激活区域，进一步产生精确的分割。此外，本文还提出了在基于$\psi$的K-Shot设置下学习不同支持度图像的融合权值，旨在为查询分支提供更好的指导。

2.1 基学习器（bace learner）

首先，给定一个查询图像${\mathbf{x}}^q\in {\mathbb{R}}^{3\times H\times W}$，先应用编码器网络$\epsilon$和卷积块提取中间特征映射${\mathbf{f}}_b^q$，上述过程的公式表达如下：

$${\mathbf{f}}_b^q={\mathcal{F}}_{conv}(\epsilon ({\mathbf{x}}^q))\in {\mathbb{R}}^{c\times h\times w}\text{\hspace{1em}(1)}$$
其中，${\mathcal{F}}_{conv}$表示连续的卷积操作，$c,h,w$分别为通道数、高和宽。

随后，解码器网络${\mathcal{D}}_b$会逐步扩大中间特征映射${\mathbf{f}}_b^q$的空间尺度，最后给出预测结果，公式表达如下：

$${\mathbf{p}}_b=\text{softmax}({\mathcal{D}}_b({\mathbf{f}}_b^q))\in {\mathbb{R}}^{(1+N_b)\times H\times W}\text{\hspace{1em}(2)}$$
其中，$\text{softmax}(\cdot )$沿着通道逐维操作以产生概率映射${\mathbf{p}}_b$，$N_b$代表基类的种类数。

与小样本场景中，广泛采用的基于episodic learning的范式不同，本文遵循标准的监督学习范式来训练基学习器。这里使用交叉熵（CE） 损失来评估${\mathbf{p}}_b和ground-truth{\mathbf{m}}_b^q$在所有空间位置上的差异，其可以表示为：

$${\mathcal{L}}_{base}={\frac{1}{n}}_{bs}\sum _{\begin{array}{c}i=1\end{array}}^{\begin{array}{c}{n}_{bs}\end{array}}\text{CE}({\mathbf{p}}_{b;i},{\mathbf{m}}_{b;i}^q)\text{\hspace{1em}(3)}$$
其中，$n_{bs}$是每个batch中训练样本的数量。

为什么不将两个学习器一起训练呢？作者认为，先进的FSS方法通常在训练期间冻结骨干网络以增强泛化能力。这样的操作与标准分割模型的学习方法不一致，无疑会影响基学习器的学习性能。更重要的是，基于episodic learning的范式能否很好地训练基学习器尚不清楚，因此本文最终采用了两阶段的训练策略。

2.2 元学习器（meta learner）

给定一个支持集（Support Set）$\mathcal{S}=\{{\mathbf{x}}^s,{\mathbf{m}}^s\}$和一个查询图像\bold{x}^q，我们首先连接了$block2$和$block3$的特征。随后，我们使用了$1\times 1$的卷积以减少通道维数从而生成中间特征映射：

$${\mathbf{f}}_m^s={\mathcal{F}}_{1\times 1}(\epsilon ({\mathbf{x}}^s))\in {\mathbb{R}}^{c\times h\times w}\text{\hspace{1em}(4)}$$

$${\mathbf{f}}_m^q={\mathcal{F}}_{1\times 1}(\epsilon ({\mathbf{x}}^q))\in {\mathbb{R}}^{c\times h\times w}\text{\hspace{1em}(5)}$$

其中，$\epsilon$是基学习器和元学习器共享的编码网络，${\mathcal{F}}_{1\times 1}$表示将输入特征编码到256维的$1\times 1$卷积。

此外，我们通过掩膜平均池化操作[3]（masked average pooling, MAP） 来提供关键的类相关提示：

$${\mathbf{v}}_s={\mathcal{F}}_{\text{pool}}({\mathbf{f}}_m^s\odot \mathcal{I}({\mathbf{m}}^s))\in {\mathbb{R}}^c\text{\hspace{1em}(6)}$$
其中，${\mathcal{F}}_{\text{pool}}$表示平均池化操作，$\odot$表示阿达玛乘积，$\mathcal{I}$是一个函数，它通过插值和扩展技术将${\mathbf{m}}^s$重塑为与${\mathbf{f}}_m^s$相同的形状，使$\mathcal{I}：{\mathbb{R}}^{H\times W}\to {\mathbb{R}}^{c\times h\times w}$。之后，在$v_s$的引导下激活${\mathbf{f}}_m^q$中的目标区域，通过解码器网络生成最终的预测结果，上述过程可以概括为：
$${\mathbf{p}}_m=\text{softmax}({\mathcal{D}}_m({\mathcal{F}}_{\text{guidance}}({\mathbf{v}}_s,{\mathbf{f}}_m^q)))\in {\mathbb{R}}^{2\times H\times W}\text{\hspace{1em}(7)}$$
其中，${\mathcal{D}}_m$表示元学习器的解码网络，${\mathcal{F}}_{\text{guidance}}$是 FSS 的一个重要模块，它将注释信息从支持分支传递到查询分支，以提供特定的分割提示，在本文的工作中，它代表“扩展和连接”。与基学习器部分相似地，我们通过计算${\mathbf{p}}_m$和${\mathbf{m}}^q$之间的**二元交叉熵（BCE）**来更新元学习器的所有参数：
$${\mathcal{L}}_{\text{meta}}={\frac{1}{n}}_e\sum _{\begin{array}{c}i=1\end{array}}^{\begin{array}{c}{n}_e\end{array}}\text{BCE}({\mathbf{p}}_{m;i},{\mathbf{m}}_i^q)\text{\hspace{1em}(8)}$$
其中，$n_e$表示每个 batch 中训练 episode 的数量。

2.3 集成

考虑到元学习器对支持图像的质量非常敏感，我们进一步提出利用 Support-Query 图像对之间场景差异的评估结果来调整从元学习器得到的粗略预测。具体来说，我们首先整合基学习器生成的前景概率图，获得背景区域相对于少样本任务的预测：
$${\mathbf{p}}_b^f=\sum _{\begin{array}{c}i=1\end{array}}^{\begin{array}{c}{N}_b\end{array}}{\mathbf{p}}_b^i\text{\hspace{1em}(9)}$$
其中，${\mathbf{f}}_b^f$的上标$f$表示前景，下标$b$表示基学习器。

然后，利用从固定骨干网中提取的低层特征${\mathbf{f}}_{low}^s,{\mathbf{f}}_{low}^q\in {\mathbb{R}}^{C_1\times H_1\times W_1}$分别计算支持图像和查询图像的Gram矩阵（如图3）。

图3：低层特征的计算过程

请注意，这两个输入图像的相关操作是相似的，其中一个的操作可以概括为：
$${\mathbf{A}}_s={\mathcal{F}}_{\text{reshape}}({\mathbf{f}}_{low}^s)\in {\mathbb{R}}^{C_1\times N}\text{\hspace{1em}(10)}$$

$${\mathbf{G}}^s={\mathbf{A}}_s{\mathbf{A}}_s^{\mathsf{T}}\in {\mathbb{R}}^{C_1\times C_1}\text{\hspace{1em}(11)}$$

其中，$N=H_1\times W_1，{\mathcal{F}}_{\text{reshape}}$将输入的张量重塑为$C_1\times N$利用计算出的Gram矩阵，使用Frobenius 范数来评价它们之间的差异，以获得指导调整过程的总体指标$\psi$：
$$\psi =\Vert {\mathbf{G}}^s-{\mathbf{G}}^q{\Vert }_F\text{\hspace{1em}(12)}$$
其中，$\Vert \cdot {\Vert }_F$表示对输入的矩阵求 Frobenius 范数。然后，在调整因子$\psi$的指导下对两个学习器的粗预测结果进行整合，进一步得出最终的分割预测${\mathbf{p}}_f$：

$${\mathbf{p}}_f^0={\mathcal{F}}_{\text{ensemble}}({\mathcal{F}}_{\psi }({\mathbf{p}}_m^0),{\mathbf{p}}_b^f)\text{\hspace{1em}(13)}$$

$${\mathbf{p}}_f={\mathbf{p}}_f^0\oplus {\mathcal{F}}_{\psi }({\mathbf{p}}_m^1)\text{\hspace{1em}(14)}$$

其中，${\mathbf{p}}_m$和${\mathbf{p}}_b$分别表示元学习器和基学习器的预测；上标“0”和“1”分别表示背景和前景；${\mathcal{F}}_{\psi }和{\mathcal{F}}_{\text{ensemble}}$是具有特定初始参数的$1\times 1$卷积运算，前者的目标是调整元学习器的粗略结果，而后者的目标是整合两个学习器；$\oplus$表示逐通道的连接操作；最后，元训练阶段的总体损失可以通过以下方法来评估：

$$\mathcal{L}={\mathcal{L}}_{\text{final}}+\lambda {\mathcal{L}}_{\text{meta}}\text{\hspace{1em}(15)}$$

$${\mathcal{L}}_{\text{final}}={\frac{1}{n}}_e\sum _{\begin{array}{c}i=1\end{array}}^{\begin{array}{c}{n}_e\end{array}}\text{BCE}({\mathbf{p}}_i^q,{\mathbf{m}}_i^q)\text{\hspace{1em}(16)}$$

其中，$\lambda$在所有实验中都被设置成1.0，${\mathcal{L}}_{\text{meta}}$在前述元学习器中已经定义。

2.4 K-Shot 情形下的设置

当任务扩展到K-shot(K>1)时，有多个标注（支持）图像可用。目前的FSS方法通常对从支持分支中提取的原型进行平均，然后利用平均后的特征来指导后续的分割过程，该过程假设每个样本的贡献是相同的^[4,5]。然而，这种方法可能不是最优的，因为这种方法在标注图像样本与查询图像之间有显著差异的情形下，前者无法提供更有针对性的指导。因此，我们进一步提出基于调整因子 $\psi$ 的自适应估计每个支持图像的权重，其中较小的值表示较大的贡献，反之亦然。

具体来说，在给定每个支持样本的调整因子${\psi }_i$的情况下，我们首先通过连接操作将它们合并为一个统一的向量${\psi }_t\in {\mathbb{R}}^K$，然后，应用两个全连接（FC）层来生成支持图像的融合权重 $\eta$：
$$\eta =\text{softmax}({\mathbf{w}}_2^{\mathsf{T}}\text{ReLU}({\mathbf{w}}_1^{\mathsf{T}}{\psi }_t))\in {\mathbb{R}}^K\text{\hspace{1em}(17)}$$
其中，${\mathbf{w}}_1\in {\mathbb{R}}^{K\times \frac{K}{r}}$，${\mathbf{w}}_2\in {\mathbb{R}}^{\frac{K}{r}\times K}$是两个全连接层的权重，$r$表示降维因子。最后，我们做一个加权求和的操作，得到集成下最终的$\psi$参数。

2.5 扩展至广义 FSS

本文所提出的的 BAM 模型最初是为标准的 FSS 任务设计的，但它可以很容易地扩展到更一般的设置，即需要确定查询图像中基类和新类的区域。在本文的工作中，作者简单地将基学习器的结果和集成后的最终结果按照预定义的阈值\tau进行融合，得到整体分割预测${\hat{\mathbf{m}}}_{\text{g}}$，其表达式为：
$${\hat{\mathbf{m}}}_{\text{g}}^{(x,y)}=\{\begin{array}{ll}1& {\mathbf{p}}_{\text{f}}^{1;(x,y)}>\tau \\ {\hat{\mathbf{m}}}_{\text{b}}^{(x,y)}& {\mathbf{p}}_{\text{f}}^{1;(x,y)}\le \tau \text{and}{\hat{\mathbf{m}}}_{\text{b}}^{(x,y)}\ne 0\\ 0& \text{otherwise}\end{array}\text{\hspace{1em}(18)}$$
其中，$(x，y)$表示空间位置，${\hat{\mathbf{m}}}_{\text{b}}$表示基学习器的分割掩码，其可以表示为：
$${\hat{\mathbf{m}}}_{\text{b}}=\text{arg max}({\mathbf{p}}_b)\in \{0,1,...,N_b{\}}^{H\times W}\text{\hspace{1em}(19)}$$
其中，$\text{arg max}(\cdot )$沿着通道逐维执行。

03、实验

3.1 Setup

本文使用了PASCAL-5ⁱ[6] 和COCO-20ⁱ[7]两种数据集来验证模型表现。两个数据集的对象类别平均分为四个 fold，以交叉验证的方式进行实验。对于每个折叠，本文随机抽样 1000 对支持和查询图像进行验证。

训练过程可分为预训练和元训练两个阶段。第一个阶段，采用标准监督学习范式在 FSS 数据集的每个折叠上训练基学习器，这里选用的是 PSPNet^[2]模型；对于第二阶段，以 episodic learning 的方式联合训练元学习器和集成模块，在此阶段基学习器的参数是固定的，本文采用 PFENet^[4] 的一个变体作为元学习器，用 ASPP^[1] 代替 FEM 模块，以降低复杂度。

3.2 实验对比

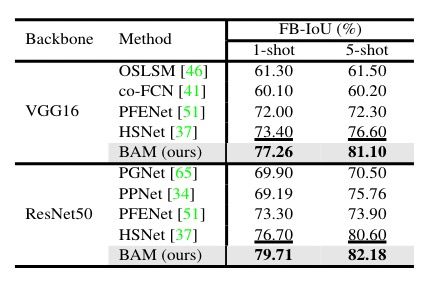
实验结果如图4、5、6所示，不难看出，无论是使用 mIoU 还是 FB-IoU，BAM模型都取得了与以往工作相比SOTA的性能。

图4：PASCAL-5ⁱ上mIoU的性能比较。“baseline”是指共享由基学习器预先训练的编码器网络的元学习器。

图5：COCO-20ⁱ在mIoU方面的性能比较。“baseline”是指在预先训练过的元学习器。

图6：PASCAL-5ⁱ上的平均FB-IoU。

3.3 定性结果

模型的可视化分割结果如图 7 所示。

图7：BAM 和 baseline 方法在One-shot设置下的定性结果。左侧来自PASCAL-5ⁱ，右侧来自COCO-20ⁱ。从上到下的每一行分别表示带有ground-truth(GT)掩码的支持图像（蓝色）、带有GT掩码的查询图像（绿色）、baseline 结果（红色）和本文结果（红色）。

04、结论

本文提出了一种新的方案来缓解 FSS 模型对已见概念的偏差问题。该方案的核心思想是利用基学习器来识别查询图像中的易混淆（基）区域，并进一步细化元学习器的预测。即使有两个普通学习者，本文的方案也在 FSS 基准上取得了 SOTA 的效果。此外，本文也将当前的任务扩展到更具挑战性的广义 FSS，并取得了较好的 baseline 结果。

参考文献

[1] Liang-Chieh Chen, George Papandreou, Iasonas Kokkinos, Kevin Murphy, and Alan L Yuille. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE transactions on pattern analysis and machine intelligence, 40(4):834–848, 2017.

[2] Hengshuang Zhao, Jianping Shi, Xiaojuan Qi, Xiaogang Wang, and Jiaya Jia. Pyramid scene parsing network. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 2881–2890, 2017.

[3] Xiaolin Zhang, Yunchao Wei, Yi Yang, and Thomas S Huang. Sg-one: Similarity guidance network for one-shot semantic segmentation. arXiv preprint arXiv:1810.09091, 2018. 2, 3, 4, 6.

[4] Zhuotao Tian, Hengshuang Zhao, Michelle Shu, Zhicheng Yang, Ruiyu Li, and Jiaya Jia. Prior guided feature enrichment network for few-shot segmentation. IEEE Transactions on Pattern Analysis & Machine Intelligence, (01):1–1, 2020.

[5] Kaixin Wang, Jun Hao Liew, Yingtian Zou, Daquan Zhou, and Jiashi Feng. Panet: Few-shot image semantic segmentation with prototype alignment. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 9197–9206, 2019.

[6] Amirreza Shaban, Shray Bansal, Zhen Liu, Irfan Essa, and Byron Boots. One-shot learning for semantic segmentation. arXiv preprint arXiv:1709.03410, 2017.

[7] Khoi Nguyen and Sinisa Todorovic. Feature weighting and boosting for few-shot segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 622–631, 2019.