利用SSA方法插值GRACE数据的空缺数据

目录

 1.SSA方法简介

2.SSA缺失值填补方法

3.基于累积分布函数(CDF)的模型选择

4.论文公开的程序包下载

5.程序包调试

---

国际各大机构发布GRACE产品存在数据空缺的问题，尤其是在GRACE和GRACE-FO之间的11个月的数据GAP，一般可以使用周期函数拟合进行数据插值,下图展示了GRACE数据缺失值的时间分布(Yi et al., 2021,JGR)。Yi and Sneeuw(2021)利用奇异谱分析的方法研究了如何对GRACE缺失的数据进行插值处理。

 1.SSA方法简介

假设有一个均匀采样的时间序列，因此其轨迹矩阵为

矩阵的列数为，Y的每个上升斜对角线都是相同的值。在之前的研究中，基于Broomhead和King(1986)提出的方法，使用矩阵Y形成滞后协方差矩阵，并采用主成分分析(PCA)程序进行处理。一种等效但更简洁的替代方法是通过奇异值分解(SVD)直接对Y进行分解:

其中的下表代表矩阵大小， 是对角矩阵，是正交的，也是滞后协方差矩阵的特征向量。主成分分析中经验正交函数(EOFs)和主成分(PCs)的输出可以表示如下：

其中和的第列，以及的第个对角线元素。请注意，如果延迟协方差矩阵定义为，则EOF和PC的定义应该交换。矩阵可以通过模态的和来重建，其中每个模态Z都等于EOF与PC的乘法:

每个模态与具有相同的结构。因此，我们可以用斜对角元素的平均值来表示一个新的时间序列，称为重构分量(RCs，记为):

其中中的所有元素满足。注意，这里的上标是位置索引。所有的总和等于原始输入时间序列:

已经按照其奇异值(即信号强度)降序排列，可以表示长期和振荡分量或噪声。因此，通常不使用包含信号(和噪声)全部信息的原始值，而是降低到的值以保留所需的:

2.SSA缺失值填补方法

SSA缺失值填补方法是利用可用样本的时间相关性来处理缺失样本的时间序列。这里，我们采用Kondrashov和Ghil(2006)提出的迭代策略。下图(Yi et al., 2021,JGR)给出了SSA缺失值填补方法的流程图。这个想法是在原来的SSA方法中添加两个循环，并逐渐迭代更新缺失值。当的假设值趋于稳定时，内层循环将停止，外层循环将逐渐增加重构序列的复杂度，复杂度由阶模数控制(式6)。初始置零，并保留更新后的值用于下一轮内外层循环。

 SSA方法有两个关键参数:窗口宽度和重建成分数，K的含义很容易理解，但参数M的影响就不那么直接了，它的值往往是由实验经验确定的。M的最优值是采用 (Khan & Poskitt, 2011)的计算方法为,其中的，因此对于GRACE的15年观测数据，其为月采样，M的取值为12月到140个月。在这里，我们从轨迹矩阵Y的角度来讨论这种情况。我们通常认为，但同样适用于，因为矩阵是转置的。在重建方程(5),每个元素的平均时间相关的滞后时间从1到M(除了端点,最大时间间隔短于M)。增大具有不同特点的相反的效果:它提高了信噪比水平高度重复的信号,而它往往抑制瞬态信号和变频振动自相关性主要存在于短延迟。从这个角度来看，较大的不一定是更好的选择。另一方面，的长度为，长度不能太小，以保证时频分析的可靠性。

RCs按方差降序排序，通常保留前几个。然而，当序列噪声很大时，前几个可能不能代表有用的信息。因此，我们提出了一个累积分布函数(CDF)测试来判断一个模式是否为噪声，只有通过测试的才会被保留。我们将在下一节中详细介绍CDF测试。

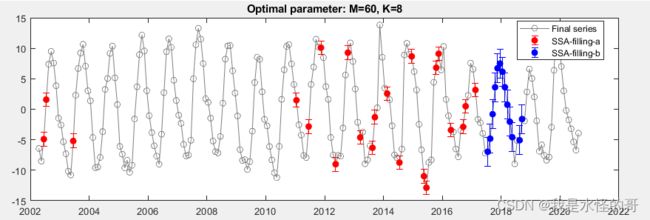
GRACE数据缺失类型可根据难度和不确定度分为SSA-filling-a和SSA-filling-b两类，GRACE内的空白标记为SSA-filling-a, GRACE- FO内11个月的空白标记为SSA-filling-b。在填充SSA-filling-b的缺失数据时，需要使用较少的数，因此我们采用了两种不同的策略。在SSA-filling-a中，我们设置所有系数M = 24, K = 12。根据我们的经验，对于一两个月的间隔来说，长达两年的相关性就足够了。通过省略不同M值(设置为整年，因为结果对M的微小变化不敏感)的一部分已知观测值的交叉验证测试表明，M = 12或24总是比较大M值更好地恢复被省略的观测值。选择K = 12总是足以保持信号，因为超过K = 12的RCs要么微不足道，要么属于高频振荡(HFOs)的范畴，因为较高的RCs通常具有较高的噪声水平。

在完成SSA-filling-a步骤后，我们将处理SSA-filling-b步骤。SSA-filling-b的M和K参数分别通过交叉验证确定每个SHC系列。在交叉验证过程中，使用了2003年至2016年的解，但我们先后遗漏了2004年至2015年的一年数据集;也就是说，我们为12个实验留出了一年的间隔。我们通过基于M和K的各种组合的SSA gap-fill方法恢复了差距，M在12个月的间隔内从12到72个月，K在1到12之间变化。用12个实验的均方根值对每组参数进行评价。当恢复值与观测值的差值达到最小时，选择M和K的最优集合。此外，交叉验证步骤得到的差异归因于SSA-filling-b结果的误差。

3.基于累积分布函数(CDF)的模型选择

SSA方法对时间序列进行分解，得到各模态的EOF和PC。对某一模态的PC进行傅里叶变换，得到其功率谱密度，再将功率谱密度按频率累加，得到频谱CDF。CDF图的形状显示了其组成频率的阶跃变化，揭示了时间序列的周期性特征。例如，在任何频率上都没有偏好的白噪声，其CDF曲线类似于对角线，这是白噪声Kolmogorov-Smirnov检验的基础(Massey Jr, 1951;Wouters & Schrama, 2007)。在这里，我们不只是拒绝白噪音:我们也拒绝HFOs(稍后定义)。这是必要的一步，因为高频信号容易受到噪声的影响。此外，目前的大多数研究很少对HFOs进行调查，主要集中在年度和半年的变化。为了减少数据噪声，牺牲高频频率是值得的。除了这两个原因外，由于缺乏周期约束，hfo将在较大的数据间隙中剧烈振荡。因此，我们提出了一个特别的准则，只保留至少90%的累积能量在频率低于每年3个周期(即周期≥4个月)的模态，这要求CDF曲线在每年3个周期的频率下超过0.9。

4.论文公开的程序包下载

在论文的网页端的附件处，我们可以找到公开分享的程序包。

跳转至相应的界面，我们可以找到对应的程序包，下载调试。

 

5.程序包调试

下载程序包进行读取，我发现代码缺失一个函数，

% [tt1,X1] = uniform_time(ser(:,1),ser(:,2), [2002,4,2020,8]);

这个函数我没有实现，但是其基本的功能是：把原来有缺失并且连续的数值给对应的缺失数据处以NaN代替。

运行结果

 

参考资料：

Yi, S., & Sneeuw, N. (2021). Filling the data gaps within GRACE missions using Singular Spectrum Analysis. Journal of Geophysical Research: Solid Earth, 126, e2020JB021227. https://doi. org/10.1029/2020JB021227