强化学习之Actor-Critic (AC, A2C, A3C, DDPG)
目录
- 1. Review Policy Gradient
- 2. Review Q-learning
- 3. Actor-Critic
- 4. Advantage Actor-Critic
- 5. A2C解决CartPole-v1
-
- 1)构建actor和critic
- 2)算法总体流程
- 3)从概率分布选择动作
- 4)Critic学习
- 5)Actor学习
- 6. A3C
- 7. PDPG (Pathwise Derivative Policy Gradient)
- 8. DDPG (Deep Determistic Policy Gradient)
- 9. DDPG解决Pendulum-v0
-
- 1)Pendulum-v0环境
- 2)算法总体流程
- 3)正太分布选择动作
- 4)Critic学习
- 5)Actor学习
在Actor-Critic里面最著名的是Asychronous Advantage Actor-Critic (A3C),而Advantage Actor-Critic是A2C。

1. Review Policy Gradient
我们先回顾一下PG:
∇ R ˉ θ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n ( ∑ t ′ = t T n γ t ′ − t r t ′ n − b ) ∇ log p θ ( a t ∣ s t ) (1) \nabla \bar R_\theta \approx \frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} \left(\sum_{t^\prime=t}^{T_n} \gamma^{t^\prime-t}r_{t^\prime}^n -b \right) \nabla \log p_\theta(a_t|s_t) \tag{1} ∇Rˉθ≈N1n=1∑Nt=1∑Tn(t′=t∑Tnγt′−trt′n−b)∇logpθ(at∣st)(1)
其中 G t n = ∑ t ′ = t T n γ t ′ − t r t ′ n G_t^n = \sum_{t^\prime=t}^{T_n} \gamma^{t^\prime-t}r_{t^\prime}^n Gtn=∑t′=tTnγt′−trt′n使得式子(1)中括号内的那一项有正有负,是正的话就增加在 s t n s_t^n stn选择 a t n a_t^n atn的概率,是负的话就减小在 s t n s_t^n stn选择 a t n a_t^n atn的概率。
然而 G t n G_t^n Gtn是很不稳定,有随机性。如在s采取a可能会得到不同的 G t n G_t^n Gtn,由于策略和环境的随机性。当采样足够多的次数这是没有问题的,但在做PG的时候我们采样其实是不够多的。
那我们能不能直接去估计G的期望值呢?如果可以那就可以用G的期望值代替采样的 G t n G_t^n Gtn值。

\\[30pt]
2. Review Q-learning
在Q-learing中我们知道有两种类型的Critic,一种是估计状态的价值函数(V值),另一种是估计状态-动作对的价值函数(Q值)。他们分别为:
V π ( s ) = E π [ G t ∣ S t = s ] = E π [ ∑ k = 0 ∞ γ k R t + k + 1 ∣ S t = s ] (2) V^\pi(s)=\Bbb E_\pi[G_t|S_t=s]=\Bbb E_\pi \left[\sum_{k=0}^\infty \gamma^k R_{t+k+1}|S_t=s \right] \tag{2} Vπ(s)=Eπ[Gt∣St=s]=Eπ[k=0∑∞γkRt+k+1∣St=s](2)
Q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] = E π [ ∑ k = 0 ∞ γ k R t + k + 1 ∣ S t = s , A t = a ] (3) Q^\pi(s,a)=\Bbb E_\pi[G_t|S_t=s,A_t=a]=\Bbb E_\pi \left[ \sum_{k=0}^\infty \gamma^k R_{t+k+1} |S_t=s,A_t=a \right] \tag{3} Qπ(s,a)=Eπ[Gt∣St=s,At=a]=Eπ[k=0∑∞γkRt+k+1∣St=s,At=a](3)

\\[30pt]
3. Actor-Critic
- 我们来思考下 G t n G_t^n Gtn的期望值 E [ G t n ] E[G_t^n] E[Gtn]是什么呢?实际上 E [ G t n ] = Q π θ ( s t n , a t n ) E[G_t^n]=Q^{\pi_\theta}(s_t^n,a_t^n) E[Gtn]=Qπθ(stn,atn),因为在公式(1)中是在状态 s t n s_t^n stn采取动作 a t n a_t^n atn所获得的累计折扣奖励,就是Q值的定义。
- 我们可以用 V π θ ( s t n ) V^{\pi_\theta}(s_t^n) Vπθ(stn)来代替baseline b b b,这是一种常用的方法。
- 另外, V π θ ( s t n ) V^{\pi_\theta}(s_t^n) Vπθ(stn)是 Q π θ ( s t n , a t n ) Q^{\pi_\theta}(s_t^n,a_t^n) Qπθ(stn,atn)的期望值,因为我们有 V π ( s ) = ∑ a π ( a ∣ s ) Q π ( s , a ) V^\pi(s)=\sum_a \pi(a|s)Q^\pi(s,a) Vπ(s)=∑aπ(a∣s)Qπ(s,a)。所以可得 ( Q π θ ( s t n , a t n ) − V π θ ( s t n ) ) (Q^{\pi_\theta}(s_t^n,a_t^n)-V^{\pi_\theta}(s_t^n) ) (Qπθ(stn,atn)−Vπθ(stn))是有正有负的。
- 从下面的更新公式可看出,我们既需要学习一个actor来决策选什么动作,又需要critic来评估V值和Q值,因此该方法是actor和critic的结合。
\\[30pt]
4. Advantage Actor-Critic
- 但是同时估计V值和Q值是很复杂的,因此我们用 r t n + V π θ ( s t + 1 n ) r_t^n+V^{\pi_\theta}(s_{t+1}^n) rtn+Vπθ(st+1n)来代替 Q π θ ( s t n , a t n ) Q^{\pi_\theta}(s_t^n,a_t^n) Qπθ(stn,atn),因为我们有:
Q π ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V π ( s ′ ) ] (4) Q^\pi(s,a)=\sum_{s^\prime,r} p(s^\prime,r|s,a)[r+\gamma V^\pi(s^\prime)] \tag{4} Qπ(s,a)=s′,r∑p(s′,r∣s,a)[r+γVπ(s′)](4) - 实际上在原始的论文中试了多种方法来替代Q值,但通过实验表明以上的替代方法是最好的(看来还是得从实验中来检验)。
-
更新方式从公式(1)变成了公式(2):
∇ R ˉ θ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n ( r t n + V π ( s t + 1 n ) − V π ( s t n ) ) ) ∇ log p θ ( a t ∣ s t ) (5) \nabla \bar R_\theta \approx \frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} \left( r_t^n+V^\pi(s_{t+1}^n) - V^\pi(s_t^n)) \right) \nabla \log p_\theta(a_t|s_t) \tag{5} ∇Rˉθ≈N1n=1∑Nt=1∑Tn(rtn+Vπ(st+1n)−Vπ(stn)))∇logpθ(at∣st)(5) -
我们使用 π \pi π(actor)与环境做互动来采样,再使用critic来评估状态的价值 V π ( s t n ) 和 V π ( s t + 1 n ) V^\pi(s_t^n)和V^\pi(s_{t+1}^n) Vπ(stn)和Vπ(st+1n),然后计算出TD-error为 ( r t n + V π ( s t + 1 n ) − V π ( s t n ) ) (r_t^n+V^\pi(s_{t+1}^n) - V^\pi(s_t^n)) (rtn+Vπ(st+1n)−Vπ(stn)),critic就是使用该误差来更新自身参数。而actor采用公式(5)来更新。

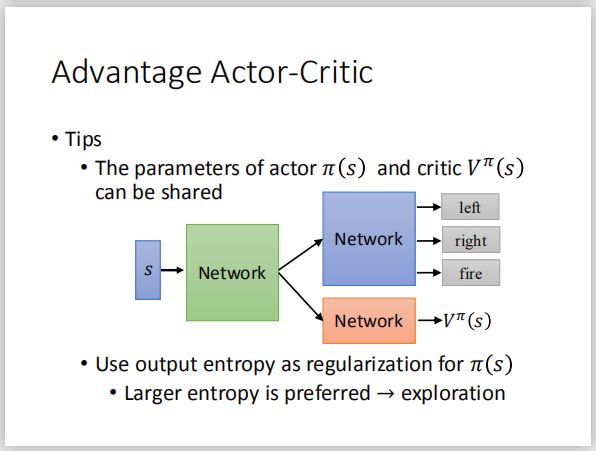
具体来说呢,critic是输入一个状态s,输出该状态的价值。而actor是输入一个状态,输出一个策略,即动作的分布。
另外我们可以对actor的输出使用entropy来regularization (正则化)来保证探索新的动作。
\\[30pt]
5. A2C解决CartPole-v1
1)构建actor和critic
我们需要建立两个网络,两个网络的输入都是状态,actor的输出是策略,而critic的输出是状态的价值。
actor = Actor(n_features=N_F, n_actions=N_A, lr=LR_A)
critic = Critic(n_features=N_F, lr=LR_C)
2)算法总体流程
- actor.choose_action(s):采用actor选择动作,具体来说是根据输出的概率分布来选择动作。actor与环境做互动来产生一个时间步的数据,因此critic和actor的学习是单步学习。
- critic.learn(s, r, s_new): 学习Critic
- actor.learn(s, a, td_error): 学习Actor
for episode in range(200):
total_reward = 0
returns = []
s = env.reset().astype(np.float32)
t = 0 # number of step in this episode
all_r = [] # rewards of all steps
for step in range(500):
a = actor.choose_action(s) #1
s_new, r, done, info = env.step(a)
s_new = s_new.astype(np.float32)
if done: break
all_r.append(r)
# Critic学习,并计算出td-error,# learn Value-function : gradient = grad[r + lambda * V(s_new) - V(s)]
td_error = critic.learn(s, r, s_new) #2
# actor学习,# learn Policy : true_gradient = grad[logPi(s, a) * td_error]
actor.learn(s, a, td_error) #3
total_reward += r
s = s_new
3)从概率分布选择动作
输入状态s,输出该状态下所有动作的概率分布,然后从概率分布随机选择动作。
# 按照分布随机动作。
def choose_action(self, s):
_logits = self.model(np.array([s]))
_probs = tf.nn.softmax(_logits).numpy()
return tl.rein.choice_action_by_probs(_probs.ravel()) # sample according to probability distribution
4)Critic学习
#1和#2: Critic网络分别计算出当前状态 s s s和下一状态 s _ s\_ s_的价值, V π ( s ) V^\pi(s) Vπ(s)和 V π ( s _ ) V^\pi(s\_) Vπ(s_)。
#3:计算出 t d _ e r r o r = r + l a m d b ∗ V π ( s _ ) − V π ( s ) td\_error =r+ lamdb * V^\pi(s\_) -V^\pi(s) td_error=r+lamdb∗Vπ(s_)−Vπ(s), 注意这里乘以了一个收益折扣lambd。
#4:我们希望这个td_error越小越好,以使得估计的价值函数越精确,因此以td_error为目标更新Critic网络。
# Critic学习,critic网络是评估状态的价值
def learn(self, s, r, s_):
v_ = self.model(np.array([s_])) #1
with tf.GradientTape() as tape:
v = self.model(np.array([s])) #2
## [敲黑板]计算TD-error
## TD_error = r + lambd * V(newS) - V(S)
td_error = r + LAMBDA * v_ - v #3
loss = tf.square(td_error) #4
grad = tape.gradient(loss, self.model.trainable_weights)
self.optimizer.apply_gradients(zip(grad, self.model.trainable_weights))
return td_error
5)Actor学习
#1:输入当前状态s到Actor中,输出动作的策略(注意未经过softmax作用)。
# Actor学习
def learn(self, s, a, td):
with tf.GradientTape() as tape:
_logits = self.model(np.array([s])) #1
## 带权重更新。
_exp_v = tl.rein.cross_entropy_reward_loss(logits=_logits, actions=[a], rewards=td[0]) #2
grad = tape.gradient(_exp_v, self.model.trainable_weights)
self.optimizer.apply_gradients(zip(grad, self.model.trainable_weights))
return _exp_v
#2:tl.rein.cross_entropy_reward_loss(logits=_logits, actions=[a], rewards=td[0])
此函数计算logits和actions之间的softmax cross entropy,然后将结果乘以权重rewards。
举个例子,假如logits=[[-4.5016805e-07, -2.3863397e-06]],action=[0],rewards=[1.0000023],该函数的计算过程如下:
- 将logits使用softmax作用得[[0.5000004840429124, 0.49999951595708747]]。
- 若actions=[0],转换成one-hot码为[[1, 0]]
- logits和actions的cross entropy为0.69314621。
- 该函数返回的结果为rewards * 0.69314621= 0.6931478。
\\[30pt]
6. A3C
7. PDPG (Pathwise Derivative Policy Gradient)

在原来的actor-critic中,critic只会告诉你采取的动作是好还是不好,而在pathwise derivative PG中会直接告诉你采取什么样的动作。
在Q-learning中我们通过Q函数来选择一个动作,现在我们使用一个actor π \pi π来选择一个动作。
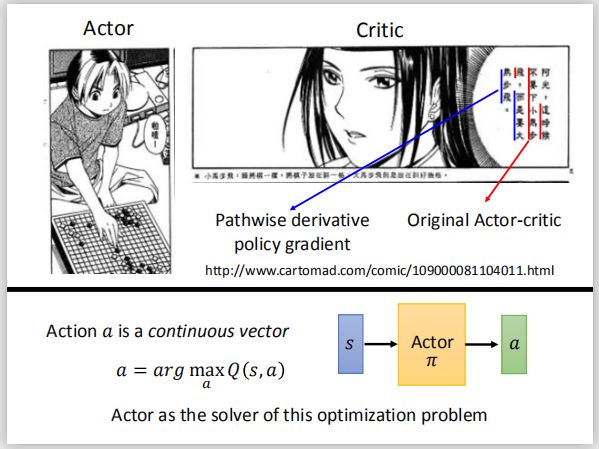
我们的Q网络的输入是状态s和采取的动作a,输出是(s,a)的Q值 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a),这里的动作a通过actor π \pi π来做选择。

下图是该算法的一个循环过程
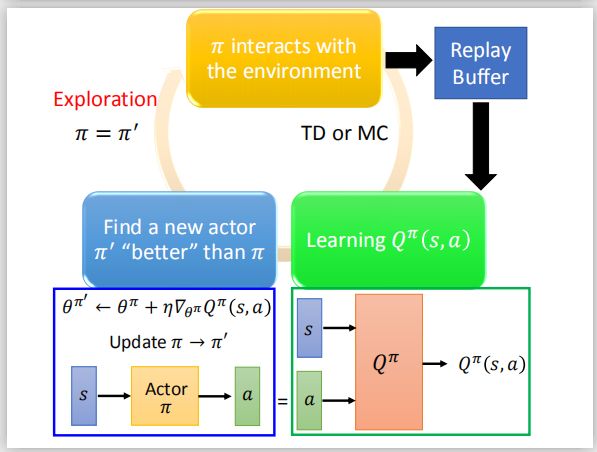
两个算法存在四个不同的地方:
- Q-learning使用Q值来选择动作,改成了使用采用actor π \pi π来选择动作。
- Q-learning使用目标Q网络来得到 max a Q ^ ( s t + 1 , a ) \max_a \hat{Q}(s_{t+1},a) maxaQ^(st+1,a)。而在这里不一样,将 s i + 1 s_{i+1} si+1和target actor π ^ ( s i + 1 ) \hat \pi(s_{i+1}) π^(si+1)合并在一起作为target Q-learning (target critic)的输入,将输出 Q ^ ( s i + 1 , π ^ ( s i + 1 ) ) \hat Q(s_{i+1},\hat \pi(s_{i+1})) Q^(si+1,π^(si+1))再加上 r i r_i ri作为我们的更新目标 y y y。
- 现在需要更新 π \pi π的参数来最大化 Q ( s i , π ( s i ) ) Q(s_i,\pi(s_i)) Q(si,π(si))。
- 每隔C步重新赋值 π ^ \hat{\pi} π^。
8. DDPG (Deep Determistic Policy Gradient)
DDPG与以上一节的PDPG的有以下不同点:
- DDPG是解决连续的控制问题,一般采用正太分布。
- 另外DDPG采用了滑动平均的机制来更新critic目标网络和actor目标网络。
9. DDPG解决Pendulum-v0
1)Pendulum-v0环境
倒立摆问题是控制问题中比较经典的问题,钟摆以随机的位置开始,动作是顺时针或逆时针调整钟摆,目标是使钟摆保持直立。
- 状态
| 序号 | 环境信息 | 最小值 | 最大值 |
|---|---|---|---|
| 1 | cos ( θ ) \cos(\theta) cos(θ) | − 1.0 -1.0 −1.0 | 1.0 1.0 1.0 |
| 2 | sin ( θ ) \sin(\theta) sin(θ) | − 1.0 -1.0 −1.0 | 1.0 1.0 1.0 |
| 3 | θ d t \theta_{dt} θdt | − 8.0 -8.0 −8.0 | 8.0 8.0 8.0 |
-
动作
动作a在 [ − 2.0 , 2.0 ] [-2.0, 2.0] [−2.0,2.0]之间取值。 -
奖励
− ( θ 2 + 0.1 ∗ θ d t 2 + 0.001 ∗ a 2 ) -(\theta^2+0.1*\theta_{dt}^2+0.001*a^2) −(θ2+0.1∗θdt2+0.001∗a2)
参考资料:https://github.com/openai/gym/wiki/Pendulum-v0
2)算法总体流程
我们重点介绍以下几个模块:
- 根据ddpg.choose_action(s)和np.clip(np.random.normal(a, VAR), -2, 2) 选择动作
- ddpg.learn():DDPG学习
for i in range(MAX_EPISODES):
t1 = time.time()
s = env.reset()
ep_reward = 0 #记录当前EP的reward
for j in range(MAX_EP_STEPS):
a = ddpg.choose_action(s) #这里很简单,直接用actor估算出a动作
a = np.clip(np.random.normal(a, VAR), -2, 2)
# 与环境进行互动
s_, r, done, info = env.step(a)
# 保存s,a,r,s_
ddpg.store_transition(s, a, r / 10, s_)
# 第一次数据满了,就可以开始学习
if ddpg.pointer > MEMORY_CAPACITY:
ddpg.learn()
#输出数据记录
s = s_
ep_reward += r #记录当前EP的总reward
在这里插入代码片
3)正太分布选择动作
- 第一行:采用actor网络估算出动作的均值。
- 第二行:np.random.normal(a, VAR)表示采用均值为a标准差为VAR的正太分布,np.clip()把采样的值约束在 [ − 2 , 2 ] [-2,2] [−2,2]之间。具体来说,若采样的值小于 − 2 -2 −2那么 a = − 2 a=-2 a=−2;若大于 2 2 2,则为 a = 2 a=2 a=2;若在 [ − 2 , 2 ] [-2,2] [−2,2]之间,则就取此值。
a = ddpg.choose_action(s) #这里很简单,直接用actor估算出a动作
a = np.clip(np.random.normal(a, VAR), -2, 2)
4)Critic学习
- #1:将下一个状态输入到actor目标网络中,输出对应的动作a_。
- #2:将下一个状态和动作a_组合后输入到critic目标网络中,输出Q值q_
- #3:计算 y = b r + GAMMA ∗ q _ y = br + \text{GAMMA} * q\_ y=br+GAMMA∗q_
这三步正好对应DDPG计算 y i y_i yi:
y i = r i + γ Q ′ ( s i + 1 , μ ′ ( s i + 1 ∣ θ μ ′ ) ∣ θ Q ′ ) y_i = r_i+\gamma Q^\prime(s_{i+1},\mu^\prime(s_{i+1}|\theta^{\mu^\prime})|\theta^{Q^\prime}) yi=ri+γQ′(si+1,μ′(si+1∣θμ′)∣θQ′)
其中 θ μ ′ \theta^{\mu^\prime} θμ′是actor目标网络 μ ′ \mu^\prime μ′的参数, θ Q ′ \theta^{Q^\prime} θQ′是critic目标网络 Q ′ Q^\prime Q′的参数。
我们看到critic更新和DQN很像,不过更新目标不是argmax了,是用critic目标网络计算出来的。 - #4:输出当前状态bs和当前状态采取的动作ba到critic网络中,得到(bs, ba)的Q值 Q ( s i , a i ∣ θ Q ) Q(s_i,a_i|\theta^Q) Q(si,ai∣θQ)。
- #5:计算真正的Q值 y i y_i yi和预测的Q值 Q ( s i , a i ∣ θ Q ) Q(s_i,a_i|\theta^Q) Q(si,ai∣θQ)之间的均方误差,计算公式如下:
L = 1 N ∑ i ( y i − Q ( s i , a i ∣ θ Q ) ) 2 L = \frac{1}{N}\sum_i (y_i-Q(s_i,a_i|\theta^Q))^2 L=N1i∑(yi−Q(si,ai∣θQ))2
# Critic:
# Critic更新和DQN很像,不过target不是argmax了,是用critic_target计算出来的。
# br + GAMMA * q_
with tf.GradientTape() as tape:
a_ = self.actor_target(bs_) #1
q_ = self.critic_target([bs_, a_]) #2
y = br + GAMMA * q_ #3
q = self.critic([bs, ba]) #4
td_error = tf.losses.mean_squared_error(y, q) #5
c_grads = tape.gradient(td_error, self.critic.trainable_weights)
self.critic_opt.apply_gradients(zip(c_grads, self.critic.trainable_weights))
5)Actor学习
- #1:将当前状态bs输出到actor网络中,输出对应的动作a。
- #2:将当前的状态bs和动作a组合在一起输入到critic网络中,就算出(bs, a)对的Q值。
- #3:求出所有样本Q值的均值作为损失函数。
# Actor:
# Actor的目标就是获取最多Q值的。
with tf.GradientTape() as tape:
a = self.actor(bs) #1
q = self.critic([bs, a]) #2
# 【敲黑板】:注意这里用负号,是梯度上升!也就是离目标会越来越远的,就是越来越大。
a_loss = -tf.reduce_mean(q) #3
a_grads = tape.gradient(a_loss, self.actor.trainable_weights)
self.actor_opt.apply_gradients(zip(a_grads, self.actor.trainable_weights))




