R语言--数据挖掘7--预测性建模:线性回归
文章目录
- 预测性建模之线性回归
-
- 模型假设
- 模型
- 理论结果
- 模型诊断
- 变量选择:
- 案例分析
-
- 数据描述
- 查看数据基本特征及其分布
- 模型拟合:
- 模型检验:
-
- 检验残差
- 异常值的检验:
- 自相关性检验:
- 多重共线性的检验:
- 总结
- 参考
- 代码
本次报告的主要目的是结合回归分析的理论来对实际mlr数据进行分析,并且分析得到的结果。
本次报告的主要内容:
- 介绍原理,介绍回归分析的原理。
- 案例分析,结合mlr.csv中的数据,使用回归模型来拟合。
- 总结,总结回归的效果。
- 参考
- 代码
预测性建模之线性回归
模型假设
- 随机误差零均值、同方差、正态性,且各个随机误差项之间相互独立。
- 随机误差项项具有正态性。
- 自变量(解释变量)是非随机的,是确定的;且各个自变量之间线性无关(不具有多重共线性)。
- 解释变量与随即项相互独立。
模型
y = α + x T β + ϵ y = \alpha + x^T \beta + \epsilon y=α+xTβ+ϵ
其中参数 α \alpha α是模型的截距项, β \beta β是回归系数变量, ϵ \epsilon ϵ是随机误差项,一般使用预测值和真实值之间的残差来估计。 β \beta β的几何意义为:当自变量 x i x_i xi增加或者减少1个单位时,自变量 y y y增加或者减少 β i \beta_i βi个单位。
理论结果
- 系数的估计值
- 预测值
- 残差的估计值
- 随机误差项方差的估计
模型诊断
-
标准化残差图(首先画图来看)
- 是否是正态
- 是否同方差(方差是否有变大、变小、变散、变集中的趋势)
-
异常值点:这会影响模型的建立。
- 来源:1 因变量上的异常:标准化残差的绝对值很大(一般是 > 2或3),2 自变量上的异常:杠杆值 H i i H_ii Hii很大。
- 识别:1 画散点图,直观判断,距离总体比较远的点。2 使用箱线图来判断是否有异常值点,并且处理,3 使用Cook距离来判断异常值,Cook距离比较大的为异常值(一般是 C o o k . d i s n a t a n c e > 4 n − k − 1 Cook.disnatance \gt \cfrac{4}{n - k -1} Cook.disnatance>n−k−14),其中Cook距离反应使用完整数据和不包含第i个观测的数据所得到拟合值的差异。
- 处理:1 删除异常值,2 保留异常值:纳入异常值分析或者做数据转换;3 可以尝试对比去除异常值和保留以尝试,同时分析,并且讨论对比其发生的原因。
-
自相关性:
- 影响:1 最小二乘依旧是无偏的,但不是有效的。2 残差的方差被明显地低估,此时做检验(t或者F)是无效的。3 最小二乘估计OLS的方差是有偏的,它低估了真实的方差和标准误差,从而导致t值变大,使得某个系数表面上显著不为零(拒绝了原假设),但事实却相反。4 R 2 R^2 R2不能反映真实的 R 2 R^2 R2。
- 检验:1 图形法:画出标准化之后的残差图,直观,但是可能不准确,2 使用DW统计量。原假设 H 0 H_0 H0:不存在自相关性,即 ρ = 0 \rho=0 ρ=0.
- 处理:在时间序列中一般使用差分法(一阶差分/二阶差分来消除);在具有自相关性的时候,尝试使用广义线性最小二乘来估计回归系数。
-
多重共线性:
-
表现:1 自变量之间的相关系数很大,2 回归系数的符号与预期的不相符合,3 预测重要的自变量的系数的标准误差很大。在极端情况下,回归模型的F检验是显著的,但是所有斜率的t值得绝对值都很小。
-
使用方差膨胀因子来检测:
V I F j = 1 1 − R j 2 VIF_j = \cfrac{1}{1 - R_j^2} VIFj=1−Rj21
其中 R j 2 R_j^2 Rj2是将第 j j j个自变量当作因变量,对其他自变量做回归得到的模型 R 2 R^2 R2.判别异常的准则:一般而言,方差膨胀因子 > 10( R j 2 > 0.9 R_j^2>0.9 Rj2>0.9),就认为存在多重共线性。
-
使用条件数来识别:
κ = p 个 自 变 量 中 相 关 系 数 矩 阵 得 最 大 特 征 值 p 个 自 变 量 中 相 关 系 数 矩 阵 得 最 小 特 征 值 \kappa = \sqrt{\cfrac{p个自变量中相关系数矩阵得最大特征值}{p个自变量中相关系数矩阵得最小特征值}} κ=p个自变量中相关系数矩阵得最小特征值p个自变量中相关系数矩阵得最大特征值判别准则:当条件数 κ \kappa κ > 15时,就认为存在多重共线性。以上的特征值:主成分所解释总体方差的比例。
-
处理:
(1) 删除部分自变量(VIF或者 κ \kappa κ大于某个常数的变量)。
(2) 对自变量进行主成分分析,选取主成分作为新的自变量。
(3) 使用变量选择法,逐步选择部分变量加入方程。
-
变量选择:
前向选择法,后向剔除法,逐步回归法(前向后向结合)得到模型,再使用AIC和BIC准则来找到最优的模型。所使用AIC和BIC的准则公式如下:
A I C p = − 2 ln ( L ^ p ) + 2 p B I C p = − 2 ln ( L ^ p ) + p log ( N ) AIC_p = -2 \ln(\hat L_p) + 2p \\ BIC_p = -2 \ln(\hat L_p) + p\log(N) AICp=−2ln(L^p)+2pBICp=−2ln(L^p)+plog(N)
其中: p p p是所考察回归模型的自变量个数, L ^ p \hat{L}_p L^p是考察模型综合训练数据的似然函数的最大值, N N N是样本、观测值的个数。
适用性:一般,BIC比AIC的惩罚更大,所选择出来的模型更小;BIC适用大样本,AIC适用于小样本。
案例分析
数据描述
本数据为wlr.csv数据,有6个变量,25个观测值。其中6个变量分别为 y , x 1 , x 2 , x 3 , x 4 , x 5 y, x1, x2, x3, x4, x5 y,x1,x2,x3,x4,x5, y y y是我们要分析的因变量,剩下的5个 x 1 , x 2 , x 3 , x 4 , x 5 x1, x2, x3, x4, x5 x1,x2,x3,x4,x5是自变量。
查看数据基本特征及其分布
有上述基本描述可知,变量前半部分比较集中,但是到上四分位数和最大值之间,几乎所有的变量的最大值都是上四分位数的一半。
再接着,可视化查看数据分布的大致情况:
 图1 x1的散点图 图1 x1的散点图
|
 图2 x2的散点图 图2 x2的散点图
|
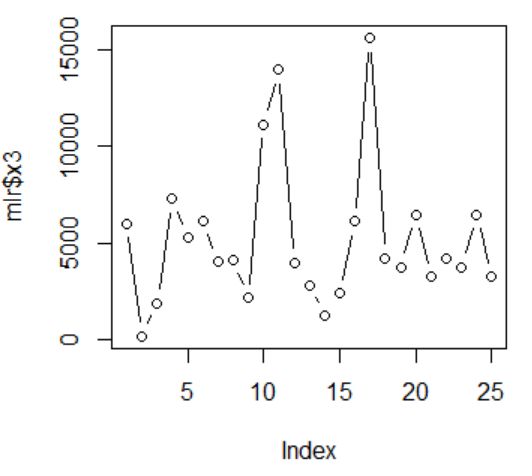 图2 x3的散点图 图2 x3的散点图
|
 图2 x4的散点图 图2 x4的散点图
|
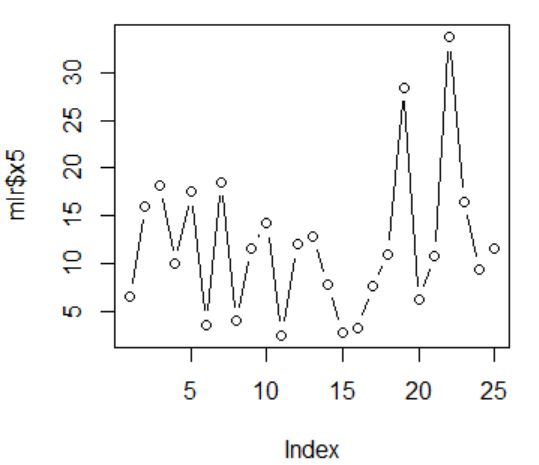 图2 x5的散点图 图2 x5的散点图
|
由上5张图片可以看出,x1第17个观测值、x2的第4个观测值、x3的第10、11、17个观测值、x4的第14、15个观测值,x5的第19、22个观测值可能为异常值点。但是总体波动不是特别大,所以我们开始适用线性模型来拟合原始数据。
模型拟合:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NNRCuYwM-1620629464962)(C:\Users\laguarange\AppData\Roaming\Typora\typora-user-images\image-20210509171540200.png)]

得到上述模型: y = 4.2604768 + 0.1273254 ∗ x 1 + 0.160566 ∗ x 2 + 0.0007636 ∗ x 3 − 0.333199 ∗ x 4 − 0.5746462 ∗ x 5 y = 4.2604768 + 0.1273254*x1 + 0.160566*x2 + 0.0007636*x3 -0.333199*x4 - 0.5746462*x5 y=4.2604768+0.1273254∗x1+0.160566∗x2+0.0007636∗x3−0.333199∗x4−0.5746462∗x5

如上结果显示,只有一个自变量x2是显著的,其他都不显著。
得到的拟合优度 R 2 R^2 R2为0.8518,调整后的 R 2 R^2 R2为0.8128也比较高,但是这并不能代表线性模型就是显著的,因此还需要对模型进行进一步地检验。
模型检验:
检验残差
-
首先对残差进行检验,以检验模型的假定条件是否满足。
先对残差标准化,画出残差的图像
 标准化残差的散点图 标准化残差的散点图
|
 标准化残差的QQ图 标准化残差的QQ图
|
由上图的左图可知,残差没有呈现处增加或者减少的趋势,因此基本认定残差是随机分布的,分布没有什么规律。
-
对残差进行正态性检验:
由上图右图,残差和认为残差服从正态分布的分位数近似一致,即散点图近似呈一条直线,所以认定残差服从正态分布。
异常值的检验:
继续对标准化之后的残差来进行检验:
 标准化残差的散点图 标准化残差的散点图
|
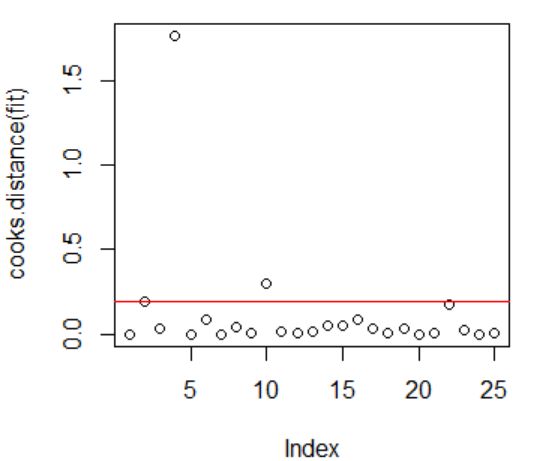 标准化残差的QQ图 标准化残差的QQ图
|
画出标准化残差之后的散点图,根据残差异常值的判定准则知道,标准化之后的残差中有两个观测值的绝对值大于2或3,这里我们初步认定其第2和第4个观测值为异常值点。其中水平红线为2,大于2代表是异常值点。
同时结合cook距离(上图的右图)来判定观测值的异常值点:得知第2、4、10个观测值为异常值点。其中水平的红线代表库克距离的边界( 4 n − k − 1 \cfrac{4}{n - k -1} n−k−14),大于红线代表是异常值点。
结合两种方法,我们尝试分别删除第2和第4个观测值来重新建立回归模型来进行分析。
 删掉第2个观测 删掉第2个观测
|
 删掉第4个观测 删掉第4个观测
|
如图所示,在删掉第2个观测值之后,在显著性上,基本山没有发生变化,还是自变量x2较为显著,变量x5一般显著。在删掉第4个观测值之后,在显著性上,自变量x5由一般显著变得较为显著。
自相关性检验:
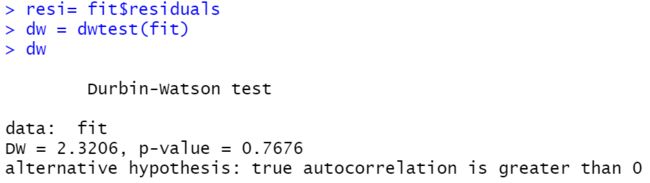
如图所示,对线性模型拟合之后的残差进行DW检验,得到p值为0.7676,不拒绝原假设。而原假设为 H 0 : ρ = 0 H_0:\rho = 0 H0:ρ=0,所以不拒绝原假设,认为残差没有自相关性。
多重共线性的检验:
这里使用方差膨胀因子VIF 来进行检验,分别得到对5个变量的方差膨胀因子为:
| x1 | x2 | x3 | x4 | x5 | |
|---|---|---|---|---|---|
| VIF | 8.233159 | 2.629940 | 5.184365 | 1.702361 | 1.174053 |
上表中所有变量的VIF均小于10,使用膨胀方差因子判别法知,不能认为变量之间存在多重共线性。
总结
所有模型在以上的检验之后,可知,除去部分的异常值点,模型基本上满足线性回归的假定。
在对异常值的处理上,对比原始保留异常值,去除第2个异常观测值,去除第4个异常的观测值,以及同时去除第2个第4个观测值,其得到的拟合优度和调整后的拟合优度得:
| 保留异常值 | 去除第2个观测 | 去除第4个观测 | 去除第2和第4个观测 | |
|---|---|---|---|---|
| R 2 R^2 R2 | 0.8518 | 0.8905 | 0.8836 | 0.9184 |
| R a d j u s t e d 2 R_{adjusted}^2 Radjusted2 | 0.8128 | 0.8601 | 0.8512 | 0.8944 |
由上表的对比可知,只要是剔除了变量,回归模型对原始数据的拟合程度都有所提高。
就单个变量而言,去除第2个观测拟合优度的提升比去除第4个观测拟合优度的提升大一些,所以,若只剔除某一个异常值变量,仅仅去除第2个观测比仅仅剔除第4个观测的效果好。
但是,若同时去除第2个第4个观测值之后,回归模型对原始数据的拟合程度达到最高。若考虑剔除异常值的方法来提高拟合优度,比较推荐同时去除第2和第4个异常值。
但是这里我还存在有一个疑惑,本案例中的观测值比较少,若比较集中,使用线性回归的拟合效果一般都比较好,可能是数据越少,拟合程度越高,具体原因还需继续收集数据,增大数据量才可以知道。将此留给以后的学习再继续去探讨。
参考
1 R语言与回归分析学习笔记(应用回归小结)(2)_beta-CSDN博客
2 R 误差自相关与DW检验 - 从前有座山,山上 - 博客园 (cnblogs.com)
3 r 语言dw检验诊断序列的自相关性_计量经济学与R语言(四)自相关_赵龙峰的博客-CSDN博客
4 多重共线性及解决方法(附R语言代码) - 知乎 (zhihu.com)
5 简单线性回归——异常值的处理 - 知乎 (zhihu.com)
6 第1章线性回归模型的自相关问题 - 百度文库 (baidu.com)
代码
##读入数据,生成R数据框mlr。
mlr <- read.csv("D:/lagua/CODING/R-learn/R-code/Chap7_PredictiveAnalysis/mlr.csv",
header = TRUE)
rownames(mlr) <- mlr[, 1]
mlr = mlr[, -1]
summary(mlr)
# 画图初步查看数据
plot(mlr$x1,type='b')
plot(mlr$x2,type='b')
plot(mlr$x3,type='b')
plot(mlr$x4,type='b')
plot(mlr$x5,type='b')
boxplot(mlr[,-c(1, 4)])
boxplot(mlr[, 4])
boxplot(scale(mlr[, -1]))
# 箱线图查看是否有异常值点
boxplot(mlr$X1)
boxplot(mlr$X2)
boxplot(mlr$X3)
boxplot(mlr$X4)
boxplot(mlr$X5)
# 模型拟合,对mlr数据集进行线性回归,
# 公式“y~x1+x2+x3+x4+x5”指出Y是因变量,x1, x2, x3, x4, x5是自变量。
fit <- lm(y~x1+x2+x3+x4+x5,mlr);fit
#查看建模结果,包括模型的拟合系数、残差、R方等信息。
summary(fit)
# 查看残差是否存在同方差,
# 查看异常值
plot(scale(fit$residuals), type='b')
abline(h=2,col='red')
## 正态性检验
qqnorm(scale(fit$residuals))
qqline(scale(fit$residuals), col="red")
# 标准化的残差,使用Cook距离画图,查看异常值点
scale(fit$residuals)
# 画残差图,查看是否满足假定
plot(cooks.distance(fit))
abline(h=4/(25-3-1), col="red")
cookdis = cooks.distance(fit)
cookdis[cookdis>4/(25-3-1)]
#取出mlr数据集中去除第2个观测值。
mlr_remove_2 <- mlr[-2, ]
mlr_remove_2 <- lm(y~x1+x2+x3+x4+x5,mlr_remove_2)
plot(scale(mlr_remove_2$residuals), type='b') # 查看残差的分布
scale(mlr_remove_2$residuals) # 查看残差的数值
summary(mlr_remove_2)
# 去除第4个观测值
mlr_remove_4 <- mlr[-4, ]
mlr_remove_4 <- lm(y~x1+x2+x3+x4+x5,mlr_remove_4)
plot(scale(mlr_remove_4$residuals), type='b')
scale(mlr_remove_4$residuals)
summary(mlr_remove_4)
# 同时去除第2和第4个观测
mlr_remove_24 <- mlr[-c(2, 4), ]
mlr_remove_24 <- lm(y~x1+x2+x3+x4+x5,mlr_remove_24)
plot(scale(mlr_remove_24$residuals), type='b')
scale(mlr_remove_24$residuals)
summary(mlr_remove_24)
# 自相关性
library(lmtest)
help(dwtest)
resi= fit$residuals
dw = dwtest(fit);dw
# 多重共线性
#计算VIF
library(car)
vif(fit)
