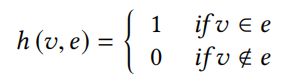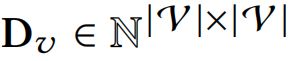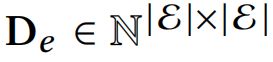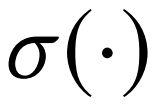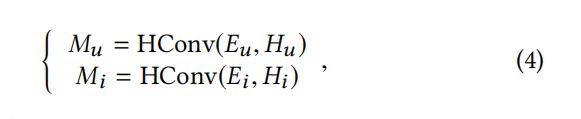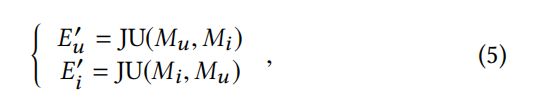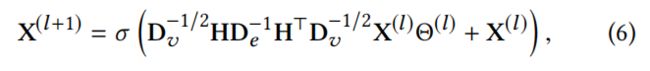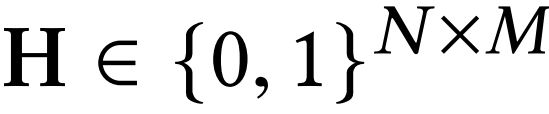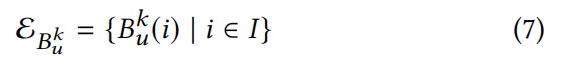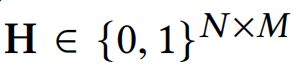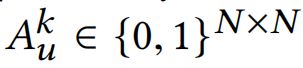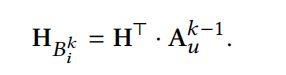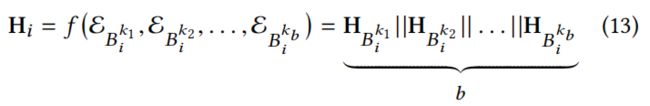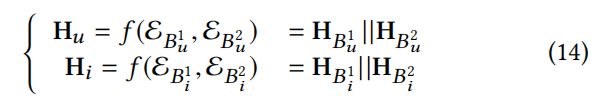【论文笔记】Dual Channel Hypergraph Collaborative Filtering ---- KDD 2020

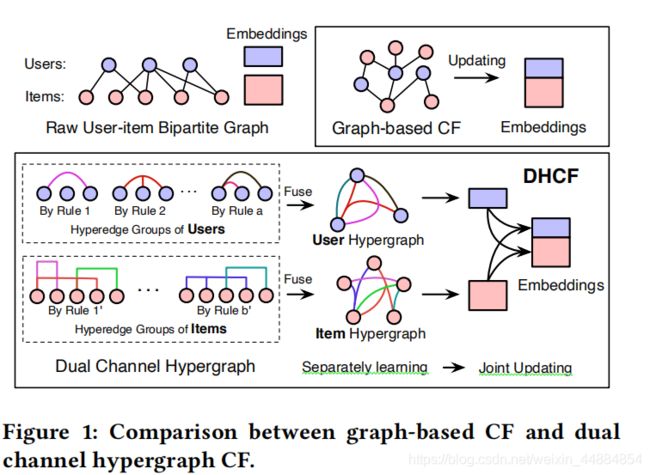
本文提出了一种新的基于超图的DHCF框架来学习用户-物品的高阶相关性，主要有两部分：高阶消息传递和联合消息更新组成。主要的亮点在于采用了一种新的图结构--超图，分别对用户和物品进行建模，并用于协同过滤中。

 

概要

协同过滤是一种最火的和最重要的推荐方法。即使被广泛采用，存在CF的模型，从矩阵分解到新兴的基于图的方法，当模型数据有限的时候表现都是比较差的。在本文中，我们首先指出了造成这种现象的两种主要主要原因：1、用户和项目建模不灵活2、实体之间的高阶相关性建模不足。在这种情况下，我们提出了一个二重的超图协同过滤(DHCF)框架来解决这种问题。首先，双通道学习策略，全面利用分而治之的策略，分别学习用户-物品的表示以至于这两种数据可以优雅的互联同时保持他们的特定属性。其次超图结构用以对用户-物品的高阶相关性建模。JHConv提出用以显式且高效的高阶关联嵌入传播。

介绍

不断增长的有价值、有吸引力和个性化的信息驱动着多种领域的多种推荐系统发展和部署。推荐系统的核心是一系列的推荐算法，这些算法根据用户的个人特点有效地筛选出爆炸性的信息。协同过滤是一种火爆且广泛应用的方法在工业和调查社区中。

总之，CF带着这个假设给用户推荐：两个行为相似的人对对物品的喜好相似。为了实现这个目标，一个标准的CF方法用下面两步：1.利用历史交互信息区分用户和物品2.基于得出的信息为特定用户生成建议

特别的，现有的CF方法被分为三类。第一种，基于用户的方法。仅仅使用用户之间的相似性，描述不同用户与同一项目交互之间关系的用户-用户相关性。类似的，基于物品的方法。仅仅使用物品-物品之间的相似性。这两种方法都只使用了历史交互数据的一部分，不可避免地承受着低劣的性能。第三种模型，包括MF和基于图的方法，不分青红皂白地整合用户和物品的交互关系用于推荐。MF使用户-物品用相同维度的向量表示。基于图的方法吧用户和物品都放入图中，能一起整合用户和物品的交互信息并最终使模型性能提高。

即使CF的方法已经过去很多年了，但是仍然有很多不足之处，尤其使训练时先验知识少的时候：

1.用户和项目建模不灵活。虽然CF方法把用户和物品建模成不可区分的点，但是用户和物品那里不存在区别。一个物品有很多交互，可以说明物品很受欢迎，但是如果一个用户有很多交互，却不能说用户很火。在这种情况下，对用户和物品进行更灵活的建模是有必要的。

2.实体之间的高阶相关性建模不足。用户 -物品之间的高阶相关性对建模是很有帮助的。现有的方法试着合并高阶相关性，因为只有成对的连接才能在图中表示，所以所采用的图结构对高阶相关建模和处理有一定的限制。

这两个问题在训练数据受限的情况下变得尤为严重。未了解决这个问题，我们提出了DHCF框架，它可以更好的学习物体-用户之间的高阶表示。未来解决用户、物品明显的表示问题。在建模过程中采用分而治之的策略，将用户和项目整合在一起，但是维持着各自的属性。特别的，如图一所示，首先对用户和物品采用了多重连接。连接生成规则可以看作了解原始数据的新视角，它可以被定义得更加灵活。例如，它可以连接两个没有之间连接却有相似行为的两个用户，这种在连接组中的关联规则能表示高阶连通性，从而导致一个超边。根据这些超边，我们可以分别为用户和物品构建两个超图。这里，一种新的跳跃超图卷积用来聚合邻居节点的信息和先前的信息，在超图上构建信息传递。

模型的大致流程：

本文的主要贡献：

1.为了学习用户、物品不同的表示，分而治之的方法被用于CF中，它可以整合用户、物品的表示用于推荐中，同时保持其特定属性，最终导致双通道协同过滤模型。

2.我们提出使用超图明确的对用户-物品之间的高阶相关性进行建模。同时提出了一个新的跳跃超图卷积JHConv方法传播表示同时包含先前的信息。

2 超图预备

 

2.1超图定义

超图，表示顶点集，代表超边集，判断顶点v是否属于超边：

对于顶点和边，它们的度表示为：

两个对角矩阵分别代表节点对角度矩阵和超边对角度矩阵：

2.2超图卷积

HGNNConv表示为：

关联矩阵为

表示可训练矩阵

表示激活函数

它也可以看作是对超图结构进行顶点-超边-顶点特征变换的两阶段细化，超图关联矩阵定义了从超边（列）到顶点（行）的消息传递路径。类似的，定义了从顶点（行）到超边（列）的消息传递路径。随后，我们定义了超图图卷积，由于两个对角矩阵在等式中用于归一化，没有消息传播，在这里不做讨论。首先，跟着的消息传递，节点特征根据超边特征聚合。随后，通过聚合它们（节点）相关的超边特征，生成优化的顶点特征。

总之，相对于图，超图含有能力建模高阶连通性除此之外，超图卷积可以通过顶点-超边-顶点获取高阶信息交互。

 

3 方法论 

在这节中，我们首先介绍了DHCF的大致模型，然后我们详细介绍了DHCF的每一个组件。

3.1DHCF通用框架

通用框架：

DHCF首先通过双通道超图结构学习用户-物品两组嵌入，随后在此基础上，DHCF通过计算用户和项目嵌入查找表的内积，进一步计算出用户项目偏好矩阵,DHCF估计一个用户对一个物品有多喜欢。

为了获取用户-物品的精准表示，DHCF使用双通道超图嵌入模型。首先，输入初始嵌入表示，随后在超图上使用两步：1.高阶消息传递2.联合消息更新

最后使用点积

3.1.1初始化

k个超边组可以分别的从自定义关联规则列表得出。除了观察到的实例直接呈现的交互作用之外，这种关联规则可以被视为描述原始数据的新视角。例如，它可以使有相似行为的没有直接联系的人联系，所以构建超边组的构建能使这种关联规则能够捕获高阶信息，而不是成对关系。

随后可以通过整合不同的超边组来生成超边关联矩阵：

3.1.2 阶段1：高阶消息传递

通过预先定义的高阶混合关系聚合邻居消息：

表示类似于HGNNConv的超图卷积操作。特别的使，HConv仅仅使消息传递函数而没有如何可以训练的参数。两个输出和分别学习了高阶邻域的复杂相关性，这里的领域是一个抽象描述，而不是直接联系，从而揭示潜在行为空间的相似性。然后我们可以分别使用和分别更新和。

3.1.3 阶段2：联合消息更新

为了提取鉴别信息，联合消息更新定位为：

方程是一个可以学习的前馈神经网络来通过后面的参数更新前面的参数。

总之，上面的两个操作构成了一层DHCF,它可以对用户、物品具有明确的高阶连通性。

 

3.2跳跃超图卷积

我们提出了一个新的超图卷积操作：

 

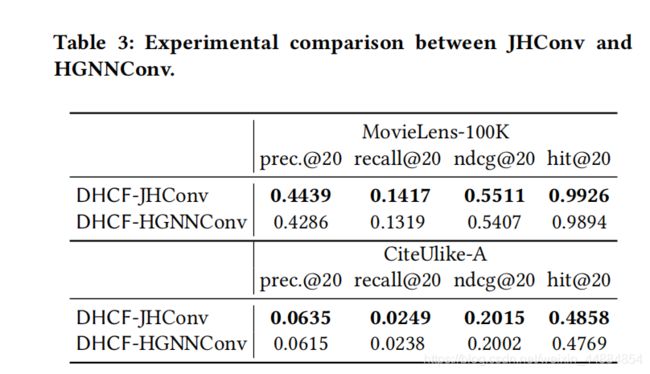
与HGNN的比较

与HGNN相比，JHConv允许模型同时考虑原始特征并且聚合相关表示，同时由于由于集成了许多附加连接，它可以避免消息稀释。

3.3高阶连通性定义

在本节中，我们介绍了一种高阶连通性在用户-物品二部图中，用户-物品二部图可以表示为

3.3.1对于用户

定义1：物品的k阶可达邻居，在用户-物品交互矩阵中，是的k阶邻居如果存在一系列相邻节点在和中，并且路径上的用户数量小于k。

定义2：物品的k阶可达用户。在用户-物品交互矩阵中，是的k阶可达如果和存在直接交互，并且是的k阶可达邻居。

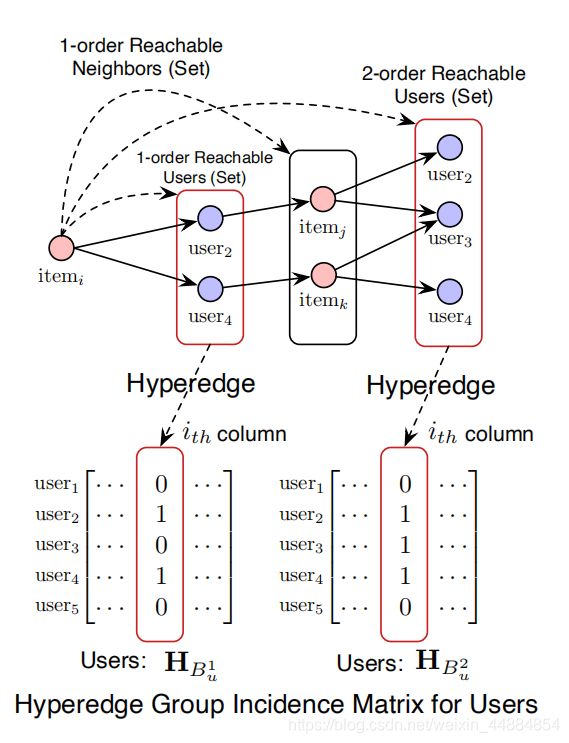
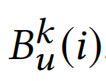对于，他的k阶可达用户集可以看作，超图可以在集合中定义，每个集都可以看作一个超边。因此，一条超边可以由k阶可达的用户集构成。然后可以在用户上构建超边组：

k阶的可达item矩阵表示为：,表示为：

表示用户-物品二部图的交互矩阵。

表示超边组交互矩阵，由用户间k阶可达规则构造而成：

通过k阶可达规则我们有一个超图组：

最后在用户上的超图关联矩阵：

3.3.2对于物品

用户的k阶可达邻居和用户的k阶可达物品可以使用相似的方法：

 

3.4DHCF层配置

3.4.1混合高阶连接的构造

对于每个用户/物品，我们分别使用k=1或者k=2捕获k阶邻居，分别为和,然后制造两种高阶连通性分别表示。然后将这两个高阶关联分别合并，构造用户/项目超图，其关联矩阵分别表示为和：

值得注意的是，提出的DHCF框架具有普遍适用性和可扩展性。换句话说，虽然我们在这里采用B1和B2来探索高阶连通性信息，但我们的模型对此没有具体的要求，这意味着其他灵活的高阶关联定义也有可能被纳入拟议的框架中。

3.4.2集成DHCF层的配置

给了用户/物品的嵌入表示和，用户Hu和项目H的超图关联矩阵，现在给高阶消息传递和联合消息更新仔细定义

阶段1：对于高阶消息传递，我们采用JHConv传播用户、物品的在超图的嵌入同时保留一定的原始信息。这里的用户表示和物品表示可以通过这种双通道方式学习。

阶段2：用于联合消息更新，我们对上一阶段的输出采用全连接神经网络，详细的配置如下：

 

传播规则的矩阵形式：

是用户物品二部图的初始交互矩阵。和是对角矩阵分别代表在超图结构中的节点度和超边度。和输入/输出用户和物品的嵌入在层。给原始的用户、物品二部图，首先在用户和项目上构造了具有混合高阶相关的超图和。随后喂入阶段1和阶段2来生成用户和物品的嵌入用于传播和链路预测。

3.5优化

在本文中我们关注于有限的隐式反馈，故使用选择逻辑优化，两两优化而不是逐点优化：

 

4 实验

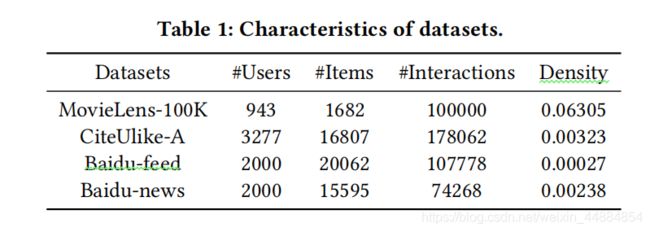
数据集

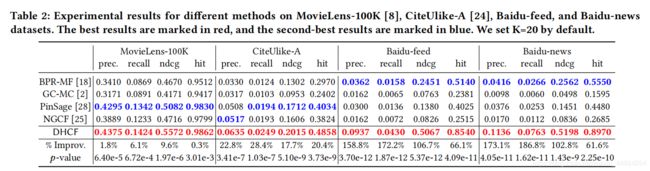
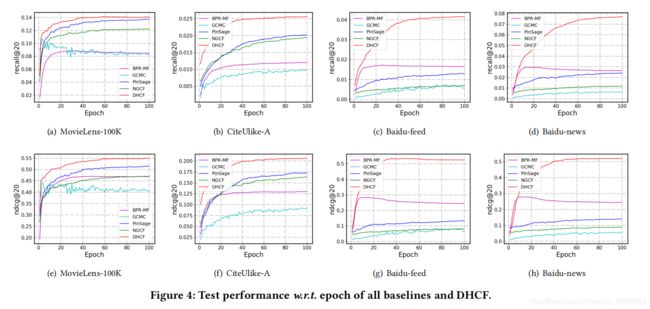
模型性能

 

 

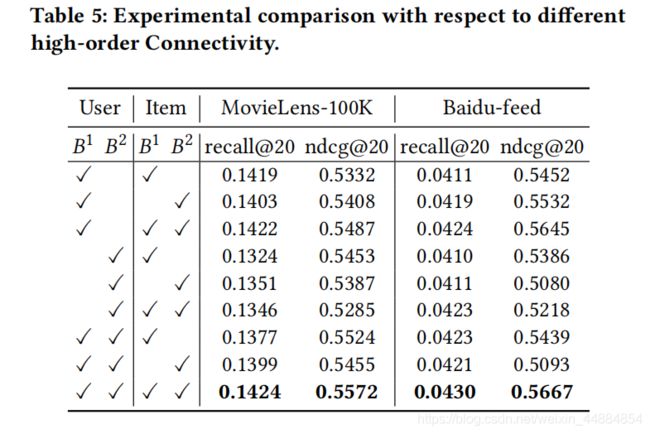
对比实验：

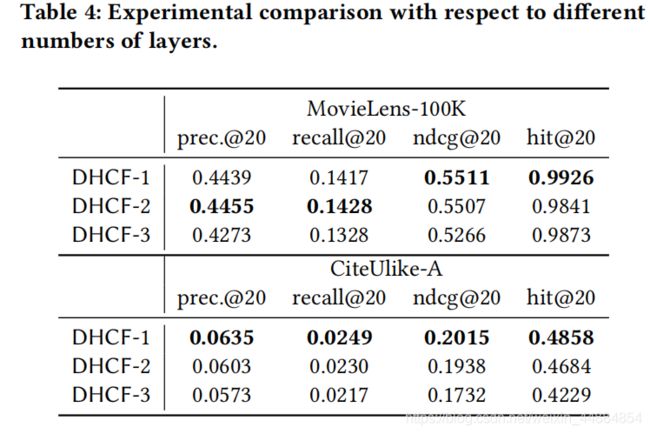
层数对比：

 

 

5 相关工作

6 结论和未来工作

在本文中，我们提出了DHCF模型，它可以对隐藏的高阶协同信号进行建模并且采用分而治之的方法解决基于隐式反馈的CF方法。我们可以得出结论：对于数据表示来说高阶信息是十分有用的并且提出的双通道超图结构是非常有效的。

未来的工作聚焦在给定义在不同交互规则的每一个超边组进行不同权重的划分来使得DHCF更加灵活。