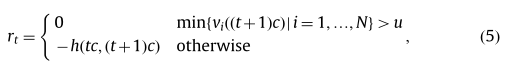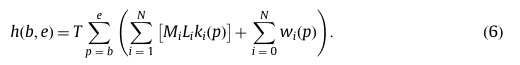交通流优化：一种强化学习方法

1. 文章信息

《Traffic flow optimization: A reinforcement learning approach》是2016年发表在Engineering Applications of Artificial Intelligence的一篇文章。

2. 摘要

交通拥堵会导致诸如延误、燃油消耗增加和额外污染等重要问题。本文提出了一种新的基于强化学习的交通流优化方法。我们证明了交通流优化问题可以表述为马尔可夫决策过程。我们使用Q-learning来学习规定高速公路上允许的最大行驶速度的政策，从而减少交通拥堵。与其他研究的重要区别：将交通预测考虑在内。

3. 引言

像自动驾驶车辆需要能够确定适当的行驶速度，同时考虑到与其他物体的距离以及道路上车辆密度增加时的潜在拥堵。智能车道保持方法需要能够对附近的车辆进行推理，这些应用程序需要自主决定如何解决问题，需要对动态和不断变化的环境做出响应，并且应该具有自适应性，即系统应该持续反映用户的偏好。所有这些特征促使在该领域引入智能软件系统，也称为智能代理。主动为高速公路指定限速还需要一个自适应控制系统，该系统可以动态响应传感器数据和交通预测。本文朝着这个方向迈出了一步，提出了一种强化学习算法，该算法根据公路的特点、占用公路的需求量以及对未来交通状况的预测，自动学习何时应为公路指定限速以减少拥堵。所得算法能够在高度复杂的领域中学习主动控制规则，并表明强化学习具有解决交通拥堵问题的潜力。

主要贡献：

第一，交通流优化问题表述为马尔可夫决策过程，并且我们表明Q-learning减少交通拥堵。

第二，文中展示了如何在我们的方法中包含交通预测。

第三，文章讨论了如何使用人工神经网络来近似定义速度限制的政策。

4. 问题定义

车辆因拥堵而导致的延误可以通过计算车辆小时数来衡量。这是一个与车辆行驶时间直接相关的指标。一辆车的小时数代表一辆车在公路上行驶1小时，但也可以解释为60辆车在高速公路上行驶1分钟。通过将所有车辆加总，可以获得总的车辆小时数。一个类似的指标是车辆总延误时间，即与自由流情况下的行驶时间相比的总附加行驶时间。例如，如果车辆在拥堵情况下的行驶时间为60分钟，而不是在自由流情况下的45分钟，则其延迟时间为15分钟。

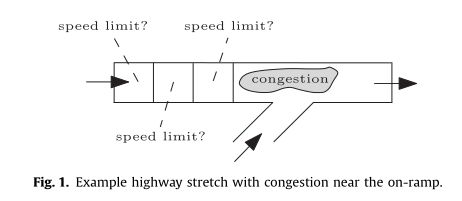
图1显示了为高速公路指定速度限制的问题，其中灰色区域表示入口匝道附近的拥挤区域，箭头指示车流方向。如果入口匝道的交通需求量很高，可以向上游路段分配限速，以减少拥堵。

然而，设定速度限制并不简单，因为很难决定何时发布速度限制，以及在哪些路段应降低公路速度。此外，应平稳增加和减少速度限制，以保护安全，并应防止速度限制的交替顺序。

5. 模型与算法

交通流模型可以分为微观和宏观两类。微观模型根据车辆的速度、位置和车辆本身的特性（例如，最大速度和加速度）定义了单个车辆的交通流行为。这些模型使建立精确的交通流模拟成为可能。

文章使用了宏观METANET模型的改编版本。METANET模型计算封闭式公路路段的速度、密度和流量值，这取决于当前交通条件以及入口匝道和出口匝道的交通需求量。自适应模型支持多车道，并包含额外的边界条件。

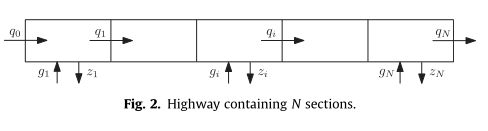
如图2所示。在模型中，T代表时间步长；ki（n）表示第i段时间nT的密度，其中n表示时间步长指数。变量vi（n）是时间nT时第i路段车辆的平均速度，变量qi（n）表示离开第i路段和进入第i路段的交通量ৰ1 t时间nT。变量Mi和Li分别表示车道数和路段i的长度。变量wi（n）表示nT时刻与路段i相关联的入口匝道的队列长度。模型的一个重要参数是拥堵交通密度kjam，达到最大占用率，速度接近零。自由流速度vf是指如果其他车辆的驾驶行为没有施加限制，则车辆的期望速度。

最优动作价值函数定义为：

最优Q值和MDP解可以使用动态规划（例如，值迭代算法）进行计算。

然而，如果转移概率和奖励值最初是未知的，那么可以应用无模型求解技术来学习策略。例如，Q-learning算法通过在环境中执行动作和观察奖励来学习Q值函数。如果代理当前处于状态s，则执行操作a以转换到另一个状态s'，并观察到奖励r，然后使用以下规则更新Q(s,a):

定义公路状态，它描述了公路在特定时间点的状态。假设速度限制在所谓的控制时间步长处发生变化。我们定义了控制时间步长Tc=c，是模拟时间步长T的倍数。这意味着，只有当METANET模拟步长是c的倍数时，才能更改速度限制。

我们让st表示模拟时间步长ct处的状态。该T表示公路的交通状况，定义如下。

第一个和第二个状态变量分别表示分配给公路的当前和以前的速度限制。在初始状态下，可设定的最大速度限制为vmax。

动作空间A包含可分配给公路路段的速度限制值，应根据交通法规和规则进行定义。AA处的动作是在模拟时间步长ct处选择的动作。动作空间示例为A={60,80, 100, 120}，这是一组可分配给公路路段的速度限制。

奖励函数可用于编码需要优化的目标函数。奖励rt取决于从时间tc到时间（t+1)c的交通状况定义如下：

其中u是阈值，阈值u可以这样定义，如果公路上的最小速度超过阈值，则不会受到惩罚。在所有其他情况下，处罚与车辆小时数成比例，h(b,e)计算METANET模拟步骤b和e之间的车辆小时数，为：

对之前描述的状态描述进行了扩展，其中还包括公路路段的预测速度和密度。修改后的状态描述如下所示，其中s0t表示模拟步骤ct的状态，该步骤使用预测信息扩展st。预测速度用v0表示，密度预测用k0表示

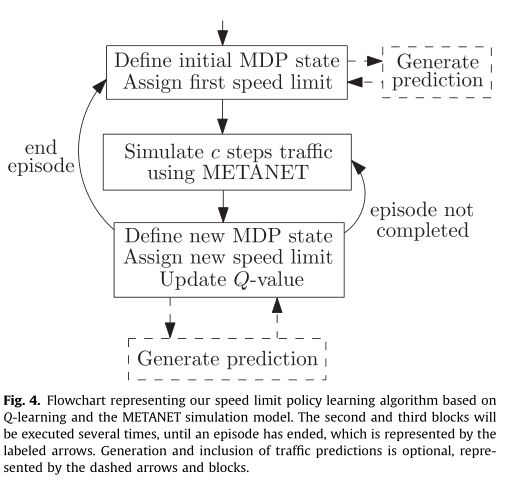
限速策略学习算法如图4的流程图所示。

该算法运行了几个Q学习片段，在此期间执行METANET模拟。当开始一集时，定义初始状态，并指定第一个速度限制（第一个区块）。然后使用METANET执行交通模拟，并考虑速度限制分配（第二个街区）。模拟后，可以定义新的MDP状态，使用公式（2）更新内存中的Q值，并指定新的速度限制（第三块）。如果情节结束，算法开始从最初的交通状态开始，并开始新的一集。在所有其他情况下，它继续这一集并运行METANET模拟。这些条件步骤由标记的箭头表示。未来公路状态的预测也可以包含在状态中，状态可视为可选步骤（虚线块）。

在学习限速策略的过程中，Q值函数被存储并更新到内存中。函数近似可用于在内存中存储近似值函数，有三个目的。首先，函数逼近器允许我们在状态空间连续时应用Q学习。其次，可以近似值函数，以避免状态变量数量呈指数级增长的内存需求。第三，函数逼近器提高了学习效率，因为它概括了学习经验。

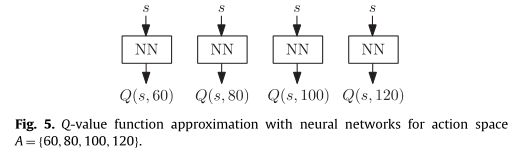
我们使用并比较了两种不同的值函数近似方法。我们使用一种称为瓦片编码的线性近似方法，这是一种系统离散状态空间的方法。我们使用的第二种方法是基于人工神经网络的值函数表示法，其中神经网络经过训练以获得值函数的期望输入-输出行为。图5给出了一个示例，其中显示了四个神经网络，对应于动作空间A={60,80,100,120}对于给定状态s，值Q(s,a)可以通过将状态变量作为输入输入到对应于动作a的神经网络来获得。

6. 实验过程

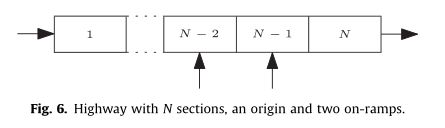
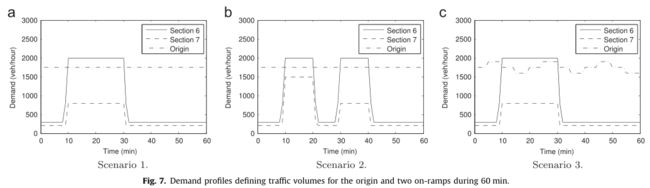
我们认为图6所示的N=8公路有两条车道，每段长度为3 km。表1给出了相关参数。在大多数实验中，我们使用METANET作为评估模型。METANET模型参数对应于实际公路。在每一集中，我们用步长15秒进行1小时的模拟，这意味着我们使用METANET计算241个步长。这包括初始交通状态，其中每个路段的速度和密度分别为120 km/h和17辆/km/车道。速度限制每5分钟改变一次，因此变量c等于20。在我们的评估中，我们考虑了三种交通情况，如图7所示。我们假设vmax等于120，动作空间为A={60，80，100，120}，速度限制仅分配给路段2-6。这些速度控制路段的选择方式使速度控制适用于第一个入口匝道附近和上游几公里处的区域。因此，它使我们能够控制接近入口匝道附近区域的车辆数量，如果入口流量较大，入口匝道可能会出现拥堵。实际上，可根据多个连续入口匝道之间的距离选择速度控制区的长度。动作空间取决于状态，因此多个连续速度限制不会交替平稳增加和减少。

我们使用Q-learning和ε-贪婪探索策略来学习策略，其中选择随机行为的概率从1线性减少到0。为了评估策略的质量，我们使用它们来控制1小时的交通流，并使用模拟中的车辆总小时数作为性能度量。比较了两种不同的值函数近似技术：瓦片编码和人工神经网络

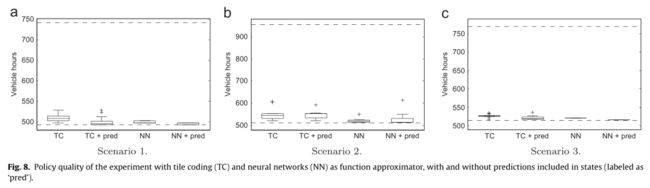
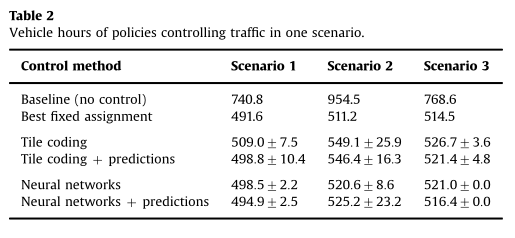
图8中的水平虚线表示最佳固定速度限制分配的车辆小时数，以及基线，即无任何速度控制的车辆小时数量。最佳固定限速分配和基线值也如表2所示。

实验结果表明，学习策略的质量接近最佳固定分配，在状态中包含预测信息时，策略质量提高。对于每个场景，州中包含预测信息的最佳策略比州中没有预测信息的最优策略更好。

除了上一节的实验之外，还研究了以神经网络作为值函数逼近器和扩展状态描述的策略学习算法的性能。

该实验的结果也如图8和表2所示，由NN和NN预测列表示。我们的结论是，与使用分片编码和初始状态描述获得的结果相比，性能有所提高。

这也可以从表中看出，在神经网络的第二个实验中，车辆小时数始终较低。实验表明，所得到的策略能够更有效地控制流量。此外，我们得出的结论是，在状态中包含预测是有益的，因为在大多数情况下，它会带来更好的性能。

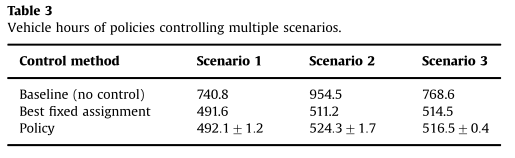
先前实验中的策略是基于一个流量场景学习的。为了降低过度匹配的风险，还可以通过按顺序运行不同场景的片段来学习策略。在这个实验中，我们使用策略学习算法来学习20个策略。每个策略在10000个学习片段中按三个场景顺序进行培训，因此每个策略的片段总数为30000。对于每个场景，策略都用于运行速度控制的交通模拟，车辆小时数再次用作性能指标。评估结果如表3所示，该表显示了对场景应用20个策略后获得的结果。从表中我们可以得出结论，政策的质量仍然接近最佳固定限速分配，与基线值相比，改进是显著的。此外，实验表明，该算法能够学习更多的通用策略，这些策略可以用于在几种不同的场景中控制流量。

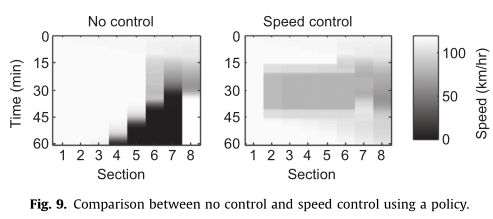
在之前的实验中，已经对策略学习算法的性能进行了分析，其中性能是使用车辆小时度量来衡量的。除了对政策质量的理论分析之外，我们还可以用图形的形式可视化政策如何控制高速公路上的交通流。在这个实验中，我们使用了一个通过我们的算法与神经网络相结合学习的政策。图9描述了场景1中高速公路上的速度如何随时间变化，其中速度用从白色到黑色的灰度表示，其中白色表示自由流，黑色表示完全拥挤的路段。左边的图片显示了如果没有限速交通管制，每个路段的速度是如何随时间变化的。右边的图片显示，路段2-6的速度可以暂时降低，以便在60分钟后解决拥堵问题。从该图中，我们得出结论，政策能够识别公路何时开始拥堵，从而可以指定适当的速度限制来减少公路拥堵。

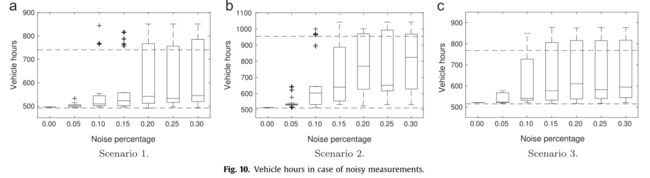
从实际道路网络中的环路检测器接收到的数据可能会受到噪声的影响。因此，我们描述了一个实验，以调查在这种不准确的测量情况下，政策是否表现良好。对于每个场景，我们运行算法以在5000集中学习策略，从而为每个场景生成一个策略。对于每个场景和噪音百分比，我们进行50次模拟，并计算每次运行的车辆小时数，以评估政策是否仍然能够适当控制交通流。图10显示了我们定义的每个场景的结果，水平虚线表示最佳固定速度限制分配的车辆小时数和基线值。从结果中我们可以得出结论，在宏观模拟中，政策对于高达10%的噪音表现良好。

之前的实验中，我们使用相同的交通流模型和模拟数据学习和评估我们的策略。为了评估其他模型的性能并解决过拟合风险，我们使用微观模拟环境进行了另一个实验。本实验的主要目的是测试如果我们将这些策略应用于不同的仿真模型（而不是METANET），这些策略是否也可以减少拥塞。

我们在城市机动能力模拟（SUMO）中实施了微观交通模拟，该模拟在单个车辆层面上模拟交通流。该实验模拟了荷兰埃因霍温一个公路立交桥附近的车辆行驶情况。我们使用OpenStreetMap中的道路网络地图，并将此数据导入SUMO。我们从包含历史交通数据的荷兰国家数据库NDW中得出了交通需求模式。这种模式是从集成在路面上的传感器和环路检测器中收集的。使用此模式，我们能够在模拟中定义类似于2013年10月21日上午7点至8点测量的实际交通量的车辆流。在我们的模拟中，我们创建了一个人工事故，导致交通减速15分钟。我们在模拟过程中使用预先计算的策略来确定适当的速度限制，并将其分配给在事故方向上游最多8公里处行驶的接近车辆。

实验重复了20次，达到了几个符合率。合规率定义有多少车辆驾驶员遵守速度限制。结果如图11所示，其中我们使用车辆小时数作为性能指标，类似于策略学习算法的评估。

从图中我们可以得出两个结论。首先，也是最重要的一点，使用METANET仿真模型学习到的政策具有足够的通用性，可以减少其他道路网络中的拥堵，与用于学习的模型不同。其次，如果只有有限的合规性（例如20%），那么与没有任何速度控制的模拟相比，我们的政策已经减少了拥堵。

7. 结论与展望

本文提出了一种基于强化学习的高速公路限速分配新方法。我们将交通流优化问题定义为马尔可夫决策过程，并应用Q-learning寻找分配速度限制的策略。与现有工作相比，文章还表明可以考虑预测信息。在算法的性能方面，我们已经证明了人工神经网络能够有效地学习策略。仿真实验表明，在基于小型道路网络的简单场景中，所得到的策略能够在高交通需求下减少交通拥堵，并且在高速公路速度和密度测量不准确的情况下，这些策略具有足够的鲁棒性。我们的实验评估表明，所提出的强化学习方法在小型道路网络中表现良好，为大规模评估提供了一个起点，在实际交通工程应用和大型道路网络中使用强化学习方法时，这是必要的。

目前，对我们方法的评估是基于针对个别公路的小规模实验。然而，实践中的交通拥堵问题可能会影响多条公路或整个公路网，因为多条互连公路上的交通之间可能存在许多依赖关系。例如，减少道路网络一部分的拥堵可能会导致其他部分的拥塞。为了根据文章的方法在较大的道路网络中实现有效的拥堵减少，未来可以研究该工作如何扩展到多条公路。

Attention

欢迎关注微信公众号《当交通遇上机器学习》！如果你和我一样是轨道交通、道路交通、城市规划相关领域的，也可以加微信：Dr_JinleiZhang，备注“进群”，加入交通大数据交流群！希望我们共同进步！