机器学习——Logistic回归

一、 Logistic回归介绍

1、一些概念

• 回归：对一些数据点，用一条直线对这些点进行拟合，该线称为最佳拟合直线，这个拟合过程就叫回归。
• 主要思想：根据现有数据对分类边界线建立回归公式，以此进行分类。

2、一般过程

• 收集数据：采用任意方法收集数据
• 准备数据：由于需要进行距离计算，因此要求数据类型为数值型。另外，结构化数据格式则最佳
• 分析数据：采用任意方法对数据进行分析
• 训练算法：大部分时间用于训练，训练的目的是为了找到最佳的分类回归系数
• 测试算法：一旦训练步骤完成，分类将会很快
• 使用算法：首先，我们需要输入一些数据，并将其转换成对应的结构化数值；接着，基于训练好的回归系数就可以对这些数值进行简单的回归分析，判定它们属于哪个类别；在这之后，我们就可以在输出的类别上做一些其他分析工作

3、优缺点

• 优点：计算代价不高，易于理解和实现
• 缺点：容易欠拟合，分类精度可能不高
• 适用数据类型：数值型和标称型数据

二、基于Logistic回归和Sigmoid函数的分类

1、Sigmoid函数

• 一种阶跃函数，取值范围（0，1），可以将一个实数映射到（0，1）的区间，可以用来做二分类。具体的计算公式：
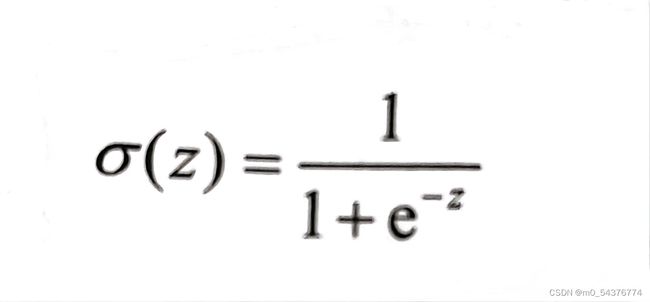
• 在不同坐标尺度下的两条曲线图：
  
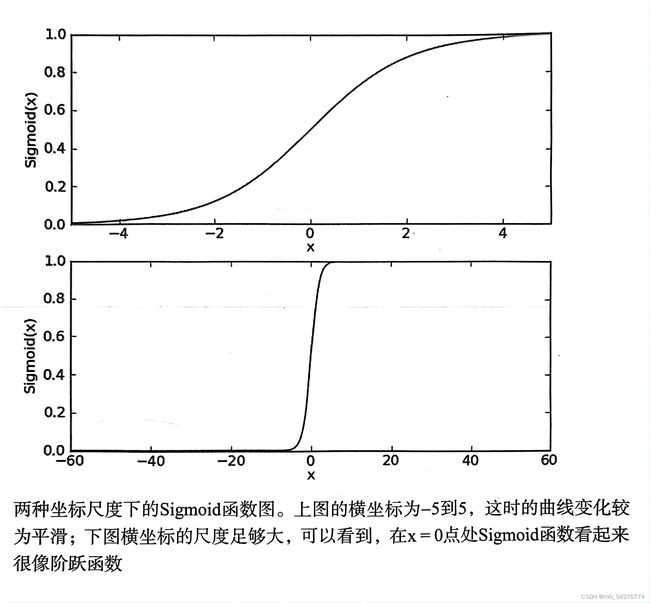
• 优点：
  （1）值域在0，1之间
  （2）函数具有很好的对称性
  （3）因为输出范围有限，所以数据在传递的过程中不容易发散，相应的缺点就是饱和的时候梯度太小
  （4）求导容易

2、Logistic回归分类器和Sigmoid函数

• 为了实现Logistic回归分类器，可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5即被归入0类。所以，Logistic回归也可以被看成是一种概率估计。
• Sigmoid函数的输入记为z,可得：
  采用向量写法： ，表示将这两个数值向量对应元素相乘然后全部加起来得到z值。其中的向量x是分类器的输入数据，向量w是我们要找到的最佳参数（系数）。

三、基于最优化方法的最佳回归系数确定

一些最优化方法：

1、梯度上升法

（1）思想

• 要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。如果梯度记为▽，则函数f(x,y)的梯度由下式表示：
  
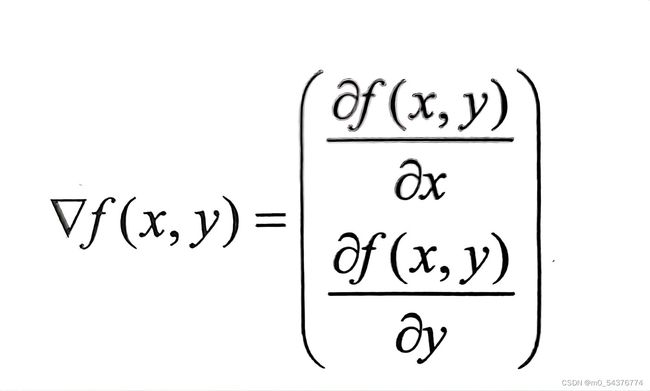
  这个梯度意味着：要沿x的方向移动 ，沿y的方向移动 。其中函数f(x,y）必须要在待计算的点上有定义且可微。

（2）公式

例子：

梯度算子总是指向函数值增长最快的方向。迭代公式如下：

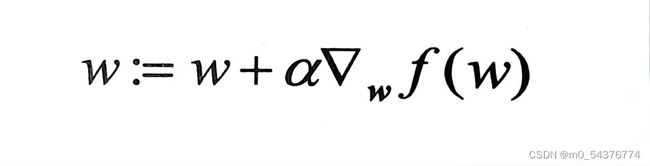
公式一直被迭代执行，直至达到某个停止条件为止，比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围。

（3）梯度下降算法

梯度下降算法和梯度上升算法一样，只是公式中的加法要变成减法。因此，对应的公式如下：

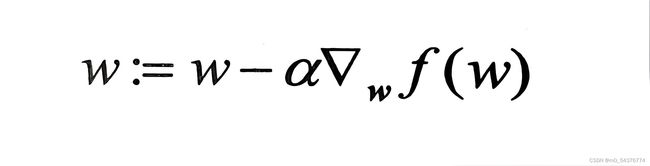
梯度上升算法用来求函数的最大值，而梯度下降算法用来求函数的最小值。

（4）随机梯度上升

梯度上升算法在每次更新回归系数时都需要遍历整个数据集，该方法在处理100个左右的数据集时尚可，但如果有数十亿样本和成千上万的特征，那么该方法的计算复杂度就太高了。一种改进方法是一次仅用一个样本点来更新回归系数，该方法称为随机梯度上升算法。由于可以在新样本到来时对分类器进行增量式更新，因而随机梯度上升算法是一个在线学习算法。与”在线学习“相对应，一次处理所有数据被称作是“批处理”。

四、梯度上升法实现

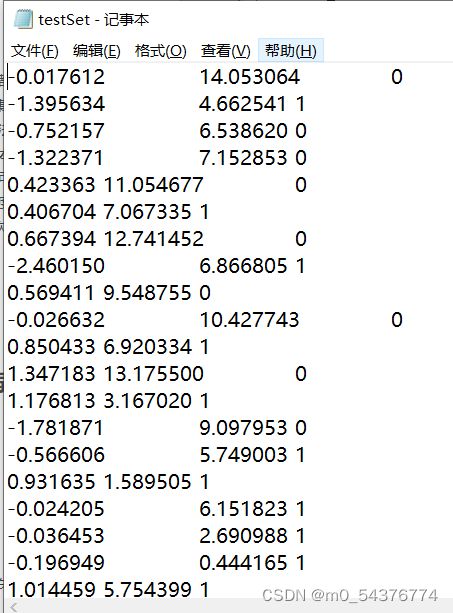
1、准备数据集

2、训练算法：使用梯度上升找到最佳参数

在上述的数据集中，100个样本点中的每个样本点包含两个特征X 1 X 2,利用梯度上升法找其最佳回归系数，也就是拟合出Logistic回归模型的最佳参数。

1、代码实现

import matplotlib.pyplot as plt
import numpy as np
 
'''
函数说明：加载数据
Parameters:
    None
Returns:
    dataMat - 数据列表
    labelMat - 标签列表
'''
def loadDataSet():
    dataMat = []  # 创建数据列表
    labelMat = []  # 创建标签列表
    fr = open('testSet.txt')  # 打开文件
    for line in fr.readlines():
        lineArr = line.strip().split()  # 去回车，放入列表
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])  # 添加数据
        labelMat.append(int(lineArr[2]))  # 添加标签
    fr.close()  # 关闭文件
    return dataMat, labelMat
'''
函数说明:sigmodi函数
Paremeters:
    inX - 数据
Returns:
    sigmoid函数
'''
def sigmoid(inX):
    return 1.0/(1 + np.exp(-inX))
 
'''
函数说明：梯度上升算法
Parameters:
    dataMatIn - 数据集
    classLables - 数据标签
Returns：
    weights.getA() - 求得的权重数组（最优参数）
'''
def gradAscent(dataMatIn, classLables):
    dataMatrix = np.mat(dataMatIn)  #转换成numpy的mat
    	    labelMat =  np.mat(classLables).transpose() #转换成numpy的mat，并进行转置
    	    m, n =np.shape(dataMatrix)#返回dataMatrix的大小。m为行，n为列
    alpha = 0.001  #移动补偿，也就是学习速率，控制更新的幅度
    maxCycles = 500 #最大迭代次数
    weights = np.ones((n,1))
   	    for k in range(maxCycles):
        h = sigmoid(dataMatrix *weights) #梯度上升矢量公式
       	        #权重系数计算公式
        error = labelMat - h
        weights = weights + alpha * dataMatrix.transpose()*error
    return weights.getA()  #将矩阵转换为数组，返回权重数组

2、测试代码

import logRegres
import matplotlib.pyplot as plt
from numpy import *

if __name__ == '__main__':

    dataArr, labelMat = logRegres.loadDataSet()
    print(logRegres.gradAscent(dataArr, labelMat))

3、结果

[[ 4.12414349]
 [ 0.48007329]
 [-0.6168482 ]]

3、分析数据：画出决策边界

已经解出了一组回归系数，确定了不同类别数据之间的分割线，那么下面就画出这条分割线，使优化过程更便于理解
1、代码实现

	'''
	函数说明：绘制数据集和Logistic回归最佳拟合直线的函数
	Parameters:
	    None
	Returns:
	    None
	'''
def plotDataSet(weights):
    dataMat, labelMat = loadDataSet()  # 加载数据集
    dataArr = np.array(dataMat)  # 转换成numpy的array数组
    n = np.shape(dataMat)[0]  # 数据个数,即行数
    xcord1 = [] ; ycord1 = []  # 正样本
    xcord2 = [] ; ycord2 = []  # 负样本
    for i in range(n):
        if int(labelMat[i]) == 1: #1为正样本
            xcord1.append(dataMat[i][1])
            ycord1.append(dataMat[i][2])
           	        else:                     #0为负样本
            xcord2.append(dataMat[i][1])
            ycord2.append(dataMat[i][2])
    	    fig = plt.figure()
    ax = fig.add_subplot(111)   #添加subplot
    ax.scatter(xcord1,ycord1,s=20,c='red',marker = 's', alpha=.5,label ='1') #绘制正样本
    ax.scatter(xcord2,ycord2,s=20,c='green',marker = 's', alpha=.5,label ='0') #绘制正样本
    x = np.arange(-3.0,3.0,0.1)
    y = (-weights[0] - weights[1] * x) / weights[2]
    ax.plot(x,y)
    plt.title('DataSet') #绘制title
    plt.xlabel('x'); plt.ylabel('y') #绘制label
    plt.legend()
    plt.show()

2、测试代码

if __name__ == '__main__':
    dataArr, labelMat = logRegres.loadDataSet()
    wigets = logRegres.gradAscent(dataArr, labelMat)
    logRegres.plotBestFit(wigets.getA())

3、结果

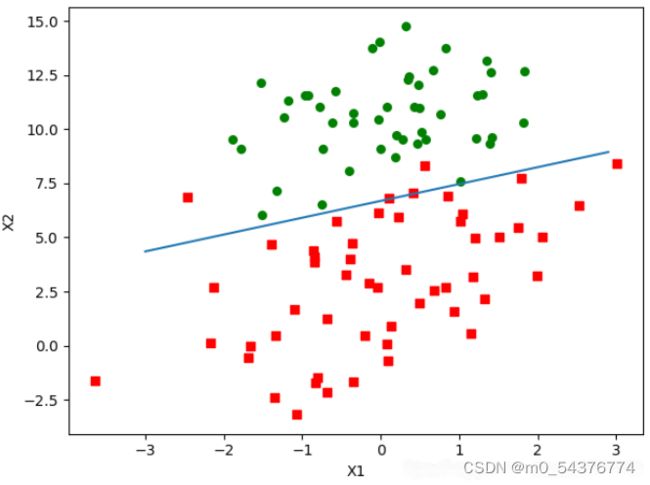
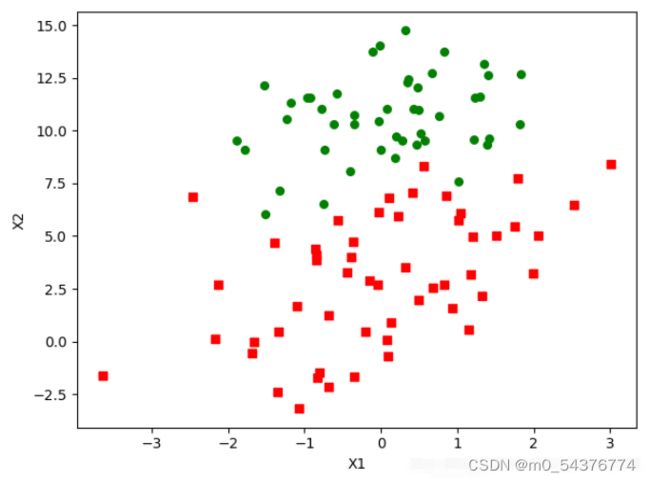
根据分类的结果来看，分类结果错分了几个点，效果已经很不错。但是尽管例子简单且数据量（100个样本点）很小，却需要大量的计算（300次乘法），但真实情况下，数据集是非常巨大的，为此应对大数据集如果采用此算法计算成本太大。将对该算法进行改进，以计算更大的数据集与特征。

4、训练算法：随机梯度上升

1、代码实现

#随机梯度上升法
def stocGradAscent0(dataMatrix, classLabels):
    m,n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)   #initialize to all ones
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    return weights

从程序代码看出，随机梯度上升算法与梯度上升算法很相似，但也存在区别：
· 后者的变量 h 和 误差 error 都是向量，而前者则是数值；
· 前者没有矩阵的转换过程，所有变量的数据类型都是 numpy 数组。
2、测试代码

if __name__ == '__main__':
    dataArr, labelMat = logRegres.loadDataSet()
    wigets = logRegres.stocGradAscent0(array(dataArr), labelMat)
    logRegres.plotBestFit(wigets)

3、结果

由图看出，此次拟合的曲线错分了1/3的样本，效果相比于梯度上升算法欠佳

五、实例——从疝气病病症预测病马的死亡率

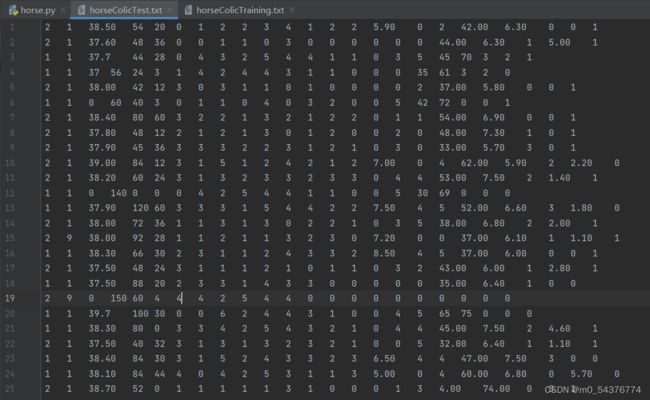
1、数据预处理

数据集存在的问题：部分数据缺失。

方法：

• 使用可用的特征的均值来填补缺失值
• 使用特殊值来填补缺失值，如-1
• 忽略有缺失值的样本
• 使用相似样本的均值填补缺失值
• 使用另外的机器学习算法预测缺失值

预处理：

• 所有的缺失值必须用一个实数值；因为Numpy数据类型不允许包含缺失值。这里选择实数0来替换所有缺失值。这样做的好处在于更新时不会影响回归系数的值，如果选择实数0来替换缺失值，那么dataMatrix的某特征对应值为0，那么该特征的系数将不做更新。所有以0代替缺失值在Logistic回归中可以满足这个要求。
• 如果在测试数据集中发现一条数据的类别标签已经缺失，那么简单做法是将该条数据丢弃，这是因为类别标签与特征不同，很难确定采用某个合适的值来替换。采用Logistic回归进行分析时这类做法是合理的。现在没有一个干净可用的数据集和一个不错的优化算法，将二者结合，预测马的生死问题。

数据集：
horseColicTraining.txt:

horseColicTest.txt:

2、测试代码：用Logistic回归进行分类

使用Logistic回归方法进行分类时，我们需要把测试集上的每个特征向量乘以最优化方法得到的回归系数，再将该乘积的结果求和，最后给Sigmoid函数即可。
如果对应的sigmoid值大于0.5，就预测类别标签为1，否则为0。

import numpy as np

# 使用逻辑回归来预测病马的死亡率

def sigmoid(inX):
	"""
	sigmoid函数
	"""
	if inX > 0:
		return 1.0 / (1 + np.exp(-inX))
	else:
		return np.exp(inX) / (1 + np.exp(inX))

def stocGradAscent1(dataMatrix, classLabels, numIter=150):
	m, n = np.shape(dataMatrix)
	weights = np.ones(n)
	for j in range(numIter):
		dataIndex = list(range(m))
		for i in range(m):
			alpha = 4 / (1.0 + j + i) + 0.01
			randIndex = int(np.random.uniform(0, len(dataIndex)))
			h = sigmoid(sum(dataMatrix[randIndex]*weights))
			error = classLabels[randIndex] - h
			weights = weights + alpha * error * dataMatrix[randIndex]
			del(dataIndex[randIndex])
	return weights

def classifyVector(inX, weights):
	prob = sigmoid(sum(inX * weights))
	if prob > 0.5:
		return 1.0
	else:
		return 0.0

def colicTest():
	frTrain = open('horseColicTraining.txt')
	frTest = open('horseColicTest.txt')
	trainingSet = []
	trainingLabels = []
	for line in frTrain.readlines():
		currLine = line.strip().split('\t')
		lineArr = []
		for i in range(21):
			lineArr.append(float(currLine[i]))
		trainingSet.append(lineArr)
		trainingLabels.append(float(currLine[21]))
	trainWeights = stocGradAscent1(np.array(trainingSet), trainingLabels, 500)
	errorCount = 0
	numTestVec = 0.0
	for line in frTest.readlines():
		numTestVec += 1.0
		currLine = line.strip().split('\t')
		lineArr = []
		for i in range(21):
			lineArr.append(float(currLine[i]))
		if int(classifyVector(np.array(lineArr), trainWeights)) != int(currLine[21]):
			errorCount += 1
	errorRate = (float(errorCount) / numTestVec)
	print("The error rate of this test is: %f" % errorRate)
	return errorRate

def multiTest():
	numTests = 10
	errorSum = 0.0
	for k in range(numTests):
		errorSum += colicTest()
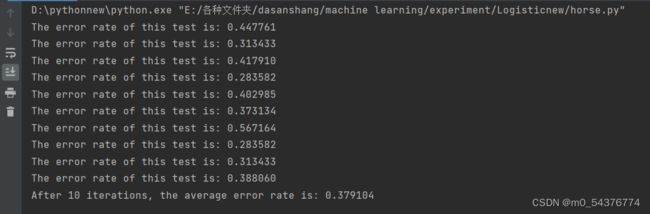
	print("After %d iterations, the average error rate is: %f" % (numTests, errorSum / float(numTests)))


def main():
	multiTest()


if __name__ == '__main__':
	main()

3、结果

由结果来看，在30%的数据缺失情况下，10次迭代之后的平均错误率是37%左右。