MATLAB2016笔记（十一）：基本粒子群优化算法（PSO）的MATLAB实现

---

一、概述

粒子群优化算法$(ParticleSwarmOptimization)$，缩写为$PSO$，属于进化算法的一种，和模拟退火算法相似，从随机解出发，通过迭代寻找最优解
$PSO$通过适应度来评价解的品质，但它比遗传算法规则更简单，没有遗传算法的“交叉”（Crossover）和“变异”（Mutation），它通过追随当前搜索到的最优值来寻找全局最优

优点：原理简单，收敛速度快
缺点：早熟收敛、维数灾难、易于陷入局部极值

知乎——粒子群算法介绍

---

二、基本原理

$PSO$从鸟群捕食模型中得到启示并可用于解决优化问题

$PSO$中，每个优化问题的潜在解都是搜索空间中的一只鸟，称为粒子
所有的粒子都有一个由被优化的函数决定的适值（$fitnessvalue$），每个粒子还有一个速度决定它们“飞行”的方向和距离
粒子们追随当前的最优粒子在解空间中搜索

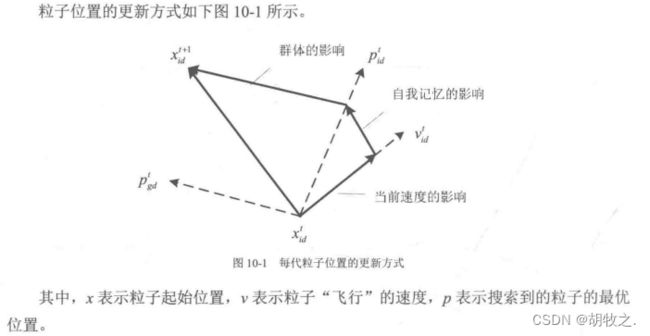
$PSO$初始化为一群随机粒子（随机解），然后通过迭代找到最优解。

在每一次迭代中，例子通过跟踪两个极值来更新自己：
一个是粒子本身找到的最优解，这个解称为个体极值；
另一个是整个种群目前找到的最优解，这个极值是全局极值，另外也可以不用整个种群，而只用其中一部分作为粒子的邻居，那么在所有邻居中的极值就是局部极值。

假设在一个$D$维的目标搜索空间中，有$N$个粒子组成一个群落，其中第$i$个粒子的位置是一个$D$维的向量:
$$X_i=(x_{i1},x_{i2},...,x_{iD}),i=1,2,...,N$$

第$i$个粒子的“飞行”速度也是一个$D$维的向量，记为:
$$V_i=(v_{i1},v_{i2},...,v_{iD}),i=1,2,...,N$$

第$i$个粒子迄今为止搜索到的最优位置称为个体极值，记为：
$$p_{best}=(p_{i1},p_{i2},...,p_{iD}),i=1,2,...,N$$

整个粒子群迄今为止搜索到的最优位置称为全局极值，记为：
$$g_{beast}=(p_{g1},p_{g2},...,p_{gD})$$

在找到这两个最优值时，粒子根据如下的公式来更新自己的速度和位置：
$$v_{id}=w\ast v_{id}+c_1{r}_1(p_{id}-x_{id})+c_2{r}_2(p_{gd}-x_{id})$$
$$x_{id}=x_{id}+v_{id}$$

所以速度可以理解为下一次迭代移动距离

其中：$c_1$和$c_2$为学习因子，也称加速常数，$r_1$和$r_2$为[0,1]范围内的均匀随机数。

$v_{id}=w\ast v_{id}+c_1{r}_1(p_{id}-x_{id})+c_2{r}_2(p_{gd}-x_{id})$由三部分组成

自左向右
第一部分为“惯性”或“动量”部分，反映粒子运动“习惯”，代表粒子有维持自己先前速度的趋势。
第二部分为“认知”部分，反映粒子对自身粒子经验的记忆或回忆，代表粒子有向自己历史最佳位置逼近的趋势。
第三部分为“社会”部分，反映了粒子间协同合作与知识共享的群体历史经验，代表粒子有向群体或邻域历史最佳位置逼近的趋势。

粒子群算法应用于多目标优化具有很大的优势，它既可以得到多目标意义下的最优解，也可以通过代表整个解集种群，按并行方式同步搜索多个非劣解，也即搜索到多个Pareto最优解（资源分配的一种理想状态）

---

三、程序设计

（一）流程

（1）初始化粒子群，包括群体规模$N$，每个粒子的位置$x_i$和速度$v_i$。
（2）计算每个粒子的适应度值$F_{it}[i]$。
（3）对每个粒子，用它的适应度值$F_{it}[i]$和个体最优值$p_{best}(i)$比较，如果$F_{it}[i]>p_{best}(i)$，则用$F_{it}[i]$替换掉$p_{best}(i)$。
（4）对每个粒子，用它的适应度值$F_{it}[i]$和全局最优值$g_{best}$比较，如果$F_{it}[i]>g_{best}$，则用$F_{it}[i]$代替$g_{best}$。
（5）更新粒子的速度$v_i$和位置$x_i$。
（6）如果满足结束条件（误差足够好或到达最大循环次数）退出，否则返回（2）。

（二）基本粒子群算法代码

在$MATLAB$中编程实现的基本粒子群算法基本函数为$PSO$，如下所示：

function [xm,fv] = PSO(fitness,N,c1,c2,w,M,D)
%基本粒子群算法
%c1 学习因子1
%c2 学习因子2
%w  惯性权重
%M  最大迭代次数
%D  搜索空间维度
%N  初始化群体个体数目

format long;%以long作为数据类型
for i=1:N
    for j=1:D
        x(i,j)=randn;  %随机初始化位置,randn,产生均值为0，方差为1的正态分布的随机数
        v(i,j)=randn;  %随机初始化速度
    end
end

%计算各个粒子的适应度，并初始化Pi（个体最优）、Pg（全局最优）
for i=1:N
    P(i)=fitness(x(i,:));
    y(i,:)=x(i,:);
end
Pg=x(N,:);

for i=1:(N-1)
    if fitness(x(i,:))<fitness(Pg)
        Pg=x(i,:);
    end
end

%进入主要循环，按照公式依次迭代，直到满足精度要求
for t=1:M
    for i=1:N
        v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(Pg-x(i,:));
        x(i,:)=x(i,:)+v(i,:);
        if fitness(x(i,:))<P(i)
            P(i)=fitness(x(i,:));
            y(i,:)=x(i,:);
        end
        if P(i)<fitness(Pg)
            Pg=y(i,:);
        end
    end
    Pbest(t)=fitness(Pg);
end

%最后给出计算结果
disp('-------------------------------')
disp('目标函数取最小值时的自变量')
xm=Pg'
disp('目标函数的最小值为：')
fv=fitness(Pg)
disp('-------------------------------')

end

（三）适应度函数——Griewank函数

格里旺克函数，是数学上常用于测试优化程序效率的函数

function y= Griewank( x )
%Griewank函数，PSO粒子群算法的适应度计算
%输入x，给出相应的y值，在x(0,0,..,0)处有全局极小点0，
[row,col]=size(x);
if row>1
    error('输入参数有误');%要求为单行
end
y1=1/4000*sum(x.^2);
y2=1;

for h=1:col
    y2=y2*cos(x(h)/sqrt(h));
end
y=y1-y2+1;
y=-y;

end

function Griewank_draw(x)
%GRIEWANK_DRAW，绘制Griewank函数图形
y=x;
[X,Y]=meshgrid(x,y);
[row,col]=size(X);
for l=1:col
    for h=1:row
        z(h,l)=Griewank([X(h,l),Y(h,l)]);
    end
end
surf(X,Y,z);
shading interp;%对曲面或图形对象的颜色着色进行色彩的插值处理，使色彩平滑过渡

end

（四）适应度函数——Rastrigin函数

Rastrigin函数，研究智能优化算法时的测试函数

function y= Rastrigin(x)
%RASTRIGIN函数
%输入x，给出相应的y值，在x(0,0,..,0)处有全局极小点0，
[row,col]=size(x);
if row>1
    error('输入参数有误');%要求为单行
end
y=sum(x.^2-10*cos(2*pi*x)+10);
y=-y;

end

function Rastrigin_draw(x)
%RASTRIGIN_DRAW,绘制Rastrigin图像
y=x;
[X,Y]=meshgrid(x,y);
[row,col]=size(X);
for l=1:col
    for h=1:row
        z(h,l)=Rastrigin([X(h,l),Y(h,l)]);
    end
end
surf(X,Y,z);
shading interp;%对曲面或图形对象的颜色着色进行色彩的插值处理，使色彩平滑过渡

end

（五）例子：求解函数最小值

$$f(x)=\sum _{i=1}^{30}(x_i^2+x_i-6)$$

1.根据函数所示，需要确定30个数，使得函数值最小，所以D也就是30；
2.目标为函数最小值，fitness函数就是此函数，且计算结果越小适应度值越高
3.可以直观看出x均为-1/2时，有最小值为-187.5

function y= fitness(x)
y=0;
for i=1:30
    y=y+x(i)^2+x(i)-6;
end
end

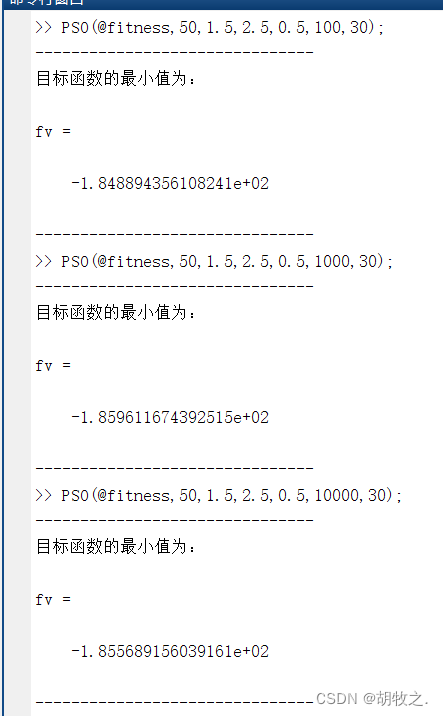
设粒子群规模$N$为50，学习因子$C_1$为1.5，学习因子$C_2$为2.5，惯性权值$w$为0.5，搜索空间维度$D$为30

先考虑最大迭代次数不同所得的结果

再考虑不同粒子群规模所得的结果

根据上图，可分析出如下结果
1.PSO为随机算法，同样的参数所得的结果也不一定一致
2.迭代步数不一定与获得解的精度成正比
3.粒子群规模越大，获得解的精度不一定越高
4.在PSO算法中，想要获得精度高的解，关键是各个参数之间的合适配合

---