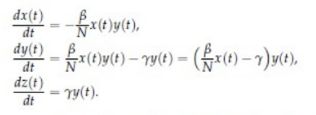生物计算：SIR模型笔记

１SIR模型

susceptible（易受感染的但没有被感染的）

infected（感染的）

recovered（恢复并免疫了的）

1.1  状态定义

第t天：

状态为S的人数	x(t)
状态为I的人数	y(t)
状态为R的人数	z(t)
总人数	N

1.2 SIR方程

这是一种形式的SIR，实际上还有很多种。

1.2.1 SIR方程解释

假设每天每个S状态的人（易受感染的但没有被感染的人）和其他m个人有关联

在第t天， 总体感染人的比例为

——>对于每一个S状态的人的这m个有关联的人里面，有 个人是感染了的

而第t天一共有x(t)个状态是S的人

——>在第t天，所有状态为S的人的x(t) × m个有关联的人里面，有个人是感染了的（这个数量不一定等于状态为I的人的数量，甚至可能比状态为I的人的数量多。因为一个感染的人可能和多个状态为S的人有关联）

假设每一个“有关联”的感染者使被关联的S状态的人被感染的概率是p

——>在第t天，新增感染者的数量为

我们令mp=β，β称之为感染接触率

那么对于S状态的人我们就有：

同时，我们令恢复率为r（也即是每天有r比例的感染者康复）

那么对于I和R状态的人我们又有：

1.3 用python实现SIR

1.3.1 导入库

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

1.3.2 数据定义

N=1000                    #总人口
I0=1                      #一开始的感染人口
R0=0                      #一开始的治愈（免疫）人口
S0=N-I0-R0                #一开始的易感染人口
beta=0.2                  #感染接触率β
gamma=0.1                 #恢复率
t=np.linspace(0,159,160)  #设置时间片段为160天

1.3.3 SIR模型定义

def sir(y,t,N,beta,gamma):
    S,I,R=y
    dS_dt=-beta*S*I/N
    dI_dt=beta*S*I/N-gamma*I
    dR_dt=gamma*I
    return(dS_dt,dI_dt,dR_dt)
#SIR常微分方程

1.3.4 进行SIR的常微分方程计算

y0=(S0,I0,R0)
#初始化参数

ret=odeint(sir,y0,t,args=(N,beta,gamma))
ret.shape
#(160, 3)

S=ret[:,0]
I=ret[:,1]
R=ret[:,2]

1.3.5 结果可视化

plt.rcParams['font.sans-serif']=['SimHei']
#用来正常显示中文

plt.rcParams['axes.unicode_minus']=False
#用来正常显示负号

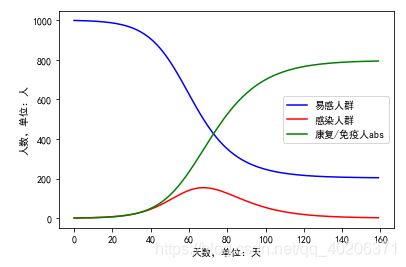
plt.plot(t,S,color='b',label='易感人群')
plt.plot(t,I,color='r',label='感染人群')
plt.plot(t,R,color='g',label='康复/免疫人abs')

plt.xlabel('天数，单位：天')
plt.ylabel('人数，单位：人')
#设置横纵轴标题

plt.legend()
#显示标签
plt.show()

2 SEIR

1、S 类，易感者 (Susceptible)，指未得病者，但缺乏免疫能力，与感染者接触后容易受到感染；

2、E 类，暴露者 (Exposed)，指接触过感染者，但暂无能力传染给其他人的人，对潜伏期长的传染病适用；

3、I 类，感病者 (Infectious)，指染上传染病的人，可以传播给 S 类成员，将其变为 E 类或 I 类成员；

4、R 类，康复者 (Recovered)，指被隔离或因病愈而具有免疫力的人。如免疫期有限，R 类成员可以重新变为 S 类。