2021-06-16 节点电压为极坐标下的牛顿-拉夫逊法潮流计算学习

节点电压用极坐标表示的牛顿-拉夫逊法的潮流计算

 当节点电压使用极坐标时，节点电压表示为：

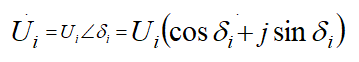
 节点功率方式表示为：


 上式将节点功率表示为节点电压的幅值和相角的函数。其中，相角差表示为两个节点电压的相角差：

 在节点电压用极坐标表示的电力系统中，假设存在n个节点的系统中，其中：
 第1个节点到第m个节点为PQ节点（其中，PQ节点为有功功率、无功功率已知，电压幅值、相角未知）；
 第m+1个节点到第n-1个节点为PV节点（其中，有功功率、电压幅值已知，无功功率、电压相角未知。那么第m+1个节点到第n-1个节点的电压幅值是已知的）；
 第n个节点为平衡节点（其中，电压幅值、相角已知，有功功率、无功功率未知。那么第n个节点的电压幅值和相角是已知的）
因此，第1个节点到第n-1个节点的电压相角是未知的，第1个节点到第m个节点的电压幅值是未知的。
 实际上，对于每一个PQ节点或者每一个PV节点都可以列些一个有功不平衡量方程式：

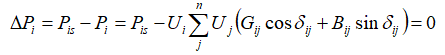
其中，i的取值范围为1，2，3，…，n-1
 对于每一个PQ节点还可以列些一个无功不平衡方程式：

其中，i的取值范围为1，2，3，…，m
 上式中一共包含n-1+m个方程式，正好同未知的电压幅值、相角的个数是相同的，相比节点电压用直角坐标系的方程式少了n-1-m个。
因此，修正方程式如下所示：

式中每个变量的具体表示为：



 在这里把节点不平衡功率对节点电压幅值的偏导数都乘以该节点的电压，相应的把节点的修正量除以该节点的电压幅值。因此，雅可比矩阵就具有比较整齐的形式。
 在对有功不平衡方程和无功不平衡方程求偏导数，可以得到雅可比元素的表达式如下：

 在使用计算机编程的过程中，计算步骤和程序框图如下所示：

 基于matlab的极坐标下的牛顿拉夫逊法潮流计算（截取重要代码）：

% 若迭代次数超过100，则跳出
for t = 1:100
    % 计算出PQ节点的不平衡量（初始化）
    % 计算节点个数
    n = nPV + nPQ + 1;
    dP = bus(1:n-1,4);
    dQ = bus(1:nPQ,5);
    % 利用for循环算出值
    % 算出有功的不平衡量以及无功不平衡量
    for i = 1:n-1
        for j = 1:n
            dP(i,1) = dP(i,1) - bus(i,2) * bus(j,2) * (real(initial_Y(i,j)) * cos(bus(i,3) - bus(j,3)) + (imag(initial_Y(i,j)) * sin(bus(i,3) - bus(j,3))));
            if i < nPQ + 1
                dQ(i,1) = dQ(i,1) - bus(i,2) * bus(j,2) * (real(initial_Y(i,j)) * sin(bus(i,3) - bus(j,3)) - (imag(initial_Y(i,j)) * cos(bus(i,3) - bus(j,3))));
            end
        end
    end
   
    % 计算出雅可比矩阵，随后进行不断的迭代
    % 当i != j时，
    %    Hij = -Ui * Uj * (Gij * sindij - Bij * cosdij)
    %    Nij = -Ui * Uj * (Gij * cosdij + Bij * sindij)
    %    Kij = Ui * Uj * (Gij * cosdij + Bij * sindij)
    %    Lij = -Ui * Uj * (Gij * sindij - Bij * cosdij)
    % 当i = j时，
    %    Hii = Ui^2 * Bii + Qi
    %    Nii = -Ui^2 * Gii -Pi
    %    Kii = Ui^2 * Gii - Pi
    %    Lii = Ui^2 * Bii -Qi
    % 首先先算H，除去平衡节点，因此是一个(n-1)*(n-1)阶矩阵，先初始化一个H矩阵
    % N是一个(n-1)*m阶矩阵，除去平衡节点,列向量主要看PQ节点的Q
    % K是一个m*(n-1)阶矩阵，除去平衡节点，行向量主要看PQ节点的Q
    % L是一个m*m阶矩阵，除去平衡节点，行和列主要看PQ节点的Q
    [nb,mb] = size(bus);
    H = zeros(nb-1,nb-1);
    N = zeros(nb-1,nPQ);
    K = zeros(nPQ,nb-1);
    L = zeros(nPQ,nPQ);
    Pi = zeros(nb-1,1);
    Qi = zeros(nb-1,1);
    % 初始化P和Q
    for i = 1:nb-1
        for j = 1:nb
            Pi(i,1) = Pi(i,1) + bus(i,2) * bus(j,2) * (real(initial_Y(i,j)) * cos(bus(i,3) - bus(j,3)) + imag(initial_Y(i,j)) * sin(bus(i,3) - bus(j,3)));
            Qi(i,1) = Qi(i,1) + bus(i,2) * bus(j,2) * (real(initial_Y(i,j)) * sin(bus(i,3) - bus(j,3)) - imag(initial_Y(i,j)) * cos(bus(i,3) - bus(j,3)));
        end
    end
    % 形成雅可比矩阵
    for i = 1 : nb-1
        for j = 1 : nb-1
            % 分别计算H矩阵的对角及非对角元素
            if i~=j 
                H(i,j) = - bus(i,2) * bus(j,2) * (real(initial_Y(i,j)) * sin(bus(i,3) - bus(j,3)) - imag(initial_Y(i,j)) * cos(bus(i,3) - bus(j,3)));
            else 
                H(i,j) = Qi(i,1) + imag(initial_Y(i,j)) * ((bus(i,2))^2);
            end
            % 分别计算N矩阵的对角及非对角元素
            if j < nPQ+1 
                if i~=j 
                    N(i,j) = - bus(i,2) * bus(j,2) * (real(initial_Y(i,j)) * cos(bus(i,3) - bus(j,3)) + imag(initial_Y(i,j)) * sin(bus(i,3) - bus(j,3))); 
                else 
                    N(i,j) = - Pi(i,1) - real(initial_Y(i,j)) * ((bus(i,2))^2); 
                end 
            end
            % 分别计算K矩阵的对角及非对角元素
            if i < nPQ+1
                if i~=j
                    K(i,j) = bus(i,2) * bus(j,2) * (real(initial_Y(i,j)) * cos(bus(i,3) - bus(j,3)) + imag(initial_Y(i,j)) * sin(bus(i,3) - bus(j,3)));
                else
                    K(i,j) = - Pi(i,1) + real(initial_Y(i,j)) * ((bus(i,2))^2); 
                end
                % 分别计算L矩阵的对角及非对角元素??
                if j < nPQ+1 
                    if i~=j 
                        L(i,j) = - bus(i,2) * bus(j,2) * (real(initial_Y(i,j)) * sin(bus(i,3) - bus(j,3)) - imag(initial_Y(i,j)) * cos(bus(i,3) - bus(j,3)));
                    else 
                        L(i,j) = - Qi(i,1) + imag(initial_Y(i,j)) * ((bus(i,2))^2); 
                    end 
                end  
            end
        end
    end
    % 雅可比矩阵形成
    J = [H N; K L];
    disp(J);
    
    % 用于计算电压的值使用
    UD = zeros(nPQ,nPQ);
    for i = 1 :nPQ 
        UD(i, i) = bus(i, 2);
    end
    tran = pinv(J);
    ALL = [dP;dQ];
    dAngU = tran * ALL;
    % 计算相角修正量 
    dAng = dAngU(1:nb-1,1);
    % 计算电压修正量 
    dU = UD * (dAngU(nb:nb+nPQ-1,1));
    % 修正电压
    bus(1:nPQ,2) = bus(1:nPQ,2) - dU;
    % 修正相角 
    bus(1:nb-1,3) = bus(1:nb-1,3) - dAng;

    % 判断是否满足精度误差，若满足则跳出，否则继续迭代
    if (max(abs(dU)) < 0.000001 && max(abs(dAng)) < 0.000001)
        break
    end
end