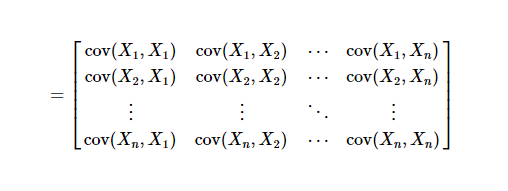协方差矩阵的定义性质与python实现
最近写统计学习的作业，要用到降维方法，一股脑把 机器学习实战 上的代码敲上去就好了，要求中还要尝试其他降维方法，查了好多发现LDA可以，但是LDA要用到计算协方差矩阵，这玩意我之前就糊里糊涂的，协方差是变量之间的，还是样本之间的，百度了numpy里的资料，又看了很多博文，这才清楚。
1.协方差定义
多维随机变量：![\boldsymbol{X}=[X_{1},X_{2}, ...,X_{n}]^{T}](http://img.e-com-net.com/image/info8/253f6dc41c4f4a56aaa39adfe8c1d3d1.gif){kind=small}
,注意是列向量，其有n个属性（或者n个变量variable、n个特征、n维），可不是n个样本！
通常我们会有一些样本，每个样本可以看成一个多维随机变量的样本点，
我们需要分析任意两个维度之间的线性关系，也就是计算各维度两两之间的协方差，
这样各协方差组成了一个n×n的矩阵，称为协方差矩阵，所以协方差矩阵的维数和样本的个数没关系！
多个样本中 ,协方差矩阵的第i行第j列元素表示第i维特征与第j维特征的协方差：
注意N指N个样本，n指每个样本有n维，此公式是标量运算, 
表示第k个样本的第i维数据，
表示所有样本的第i维数据的均值，N-1指无偏估计
协方差矩阵：
注意这里是矢量运算 nx1,1xn结果nxn，
表示第k个样本
2.协方差矩阵的性质
1）很明显，协方差矩阵是对称阵。
2）协方差矩阵为半正定矩阵，即其特征值>=0，其可以进行分解如下：
3.python的numpy.cov()函数
numpy.cov(m, y=None, rowvar=True, bias=False, ddof=None, fweights=None, aweights=None)
（1） m :array_like
包含多个变量和观察值的1-D或2-D数组。M的每一行代表一个变量（即特征），每一列都是对所有这些变量的单一观察（即每一列代表一个样本）。 另见下面的rowvar。
（2） y :array_like, optional
另外一组变量和观察结果。 y具有与m相同的形式。至于有什么作用，参考后面的实例。
（3） rowvar : bool,optional
如果rowvar为True（默认值），则每行代表一个变量，并在列中显示（即每一列为一个样本）。 否则，关系被转置：每列代表变量，而行包含观察值。
（4） bias : bool,optional
默认归一化（False）为（N-1），其中N为给定观测次数（无偏估计）。如果bias为True，则归一化为N. 这些值可以通过使用numpy版本> = 1.5中的关键字ddof来覆盖。
（5） ddof : int,optional
如果不是，偏移所隐含的默认值将被覆盖。请注意，ddof = 1将返回无偏估计，即使指定了权重和权重，ddof = 0将返回简单平均值。详见附注。 默认值为None。
（6） fweights :array_like, int, optional
整数频率权重组成的1-D数组; 代表每个观察向量应重复的次数。
（7） aweights :array_like, optional
观测矢量权重的1-D数组。对于被认为“重要”的观察，这些相对权重通常很大，而对于被认为不太重要的观察，这些相对权重较小如果ddof = 0，则可以使用权重数组将概率分配给观察向量。
python:
#x是2行3列，行数代表维数，列数代表样本个数，所以我们有3个样本，2个变量
#这和我们之前处理数据不同，之前都是行数代表样本个数，列数代表维数
#这里默认参数bias=False就是N-1,rowvar=True就是行数代表维数，列数代表样本个数
x=np.array([[1,2,9],[2,3,4]])
x
array([[1, 2, 9],
[2, 3, 4]])
np.cov(x)
array([[ 19., 4.],
[ 4., 1.]])那我们需要想让行数代表样本个数，列数代表维数，只需更改上面说的参数rowvar=False：
np.cov(样本矩阵，rowvar=False)
不用numpy也可以，用上面的x,根据上面的协方差矩阵公式
#axis=1表示对每一行求平均
z=x.mean(axis=1).reshape(2,1)
z
array([[ 4.],
[ 3.]])
y=np.dot(x-z,(x-z).T)/2
y
array([[ 19., 4.],
[ 4., 1.]])最后提醒一下一般数学公式中都是一个样本是nx1的，行数代表维数，列数代表样本个数
参考链接：
https://www.cnblogs.com/terencezhou/p/6235974.html
https://blog.csdn.net/zhuzuwei/article/details/77848323
https://www.zhihu.com/question/24283387