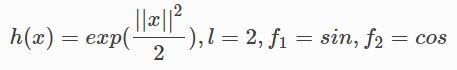Performer:Rethinking Attention with Performers(2020-9-30)
模型介绍
基于Transformer模型在众多领域已取得卓越成果,包括自然语言、图像甚至是音乐。然而,Transformer架构一直以来为人所诟病的是其注意力模块的低效,即长度二次依赖限制问题。随着输入序列长度的增加,注意力模块的问题也越来越突出,算力和内存消耗是输入序列长度的平方。
基于Transformer模型应对长输入序列
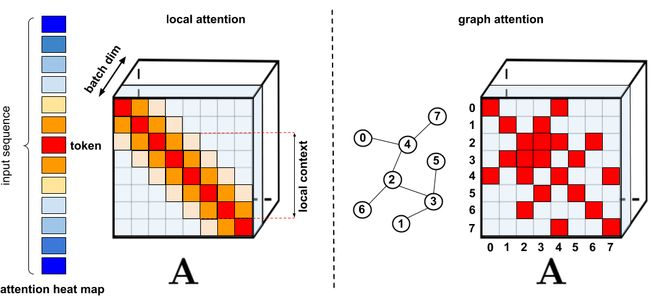
比较早期的是一方面从内存方面入手:Transformer-XL和内存压缩的Transformer,而另一种方法是各种稀疏注意力机制。稀疏注意力机制不再暴力地计算所有token之间的注意力,而仅仅计算出有限token对之间的相似度得分。这些需要重点attend的稀疏注意力项可以是人工指定,也可以是通过优化方法找到的,还可以是通过学习学到的,甚至可以是随机的。
由于稀疏矩阵也可以用图和边来表示,所以稀疏化方法也是由图神经网络文献所启发的,具体关系在图注意力网络中概述。这种基于稀疏性的架构通常需要额外的层来隐含产生完整的注意力机制。
目前的这些稀疏注意力方法仍然有以下局限:
- 需要高效的稀疏矩阵乘法运算,而这些运算并不是所有加速器都能提供。比如Longformer的实现采用TVM技术将计算自注意力的代码编译为CUDA核。
- 通常缺乏严格的理论保证。这点Big Bird是有的。
- 主要针对Transformer模型和生成式预训练进行优化。
- 通常需要堆叠更多的注意力层来补偿稀疏表征,这使得它们很难与其他预训练模型一起使用,因此需要进行再训练,这就很费时费力。
除了上述这些缺点之外,稀疏注意机制往往还无法解决常规注意力方法所应用的全部问题,比如如 Pointer Networks。此外,还有一些操作是无法进行稀疏化的,比如softmax操作。
为了解决这些问题,Performer提出了一个具有线性复杂度的注意力,其注意力机制可线性扩展,从而实现更快的训练,同时允许模型处理较长的长度,这对于某些图像数据集(如ImageNet64)和文本数据集(如PG-19)是必需的。Performer 使用一个高效的(线性)广义注意力框架(generalized attention framework),允许基于不同相似性度量(核)的一类广泛的注意力机制。该框架通过谷歌的新算法 FAVOR+( Fast Attention Via Positive Orthogonal Random Features)来实现,后者能够提供注意力机制的可扩展低方差、无偏估计,这可以通过随机特征图分解(常规 softmax-attention)来表达。该方法在保持线性空间和时间复杂度的同时准确率也很有保证,也可以应用到独立的 softmax 运算。此外,该方法还可以和可逆层等其他技术进行互操作。
两种常规的注意力机制回顾
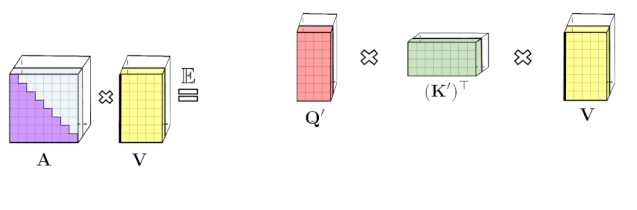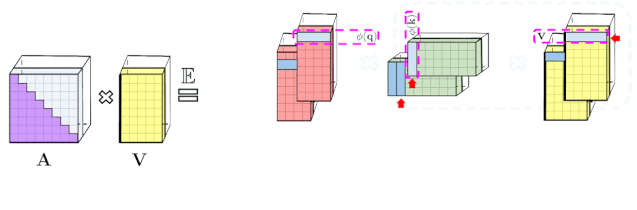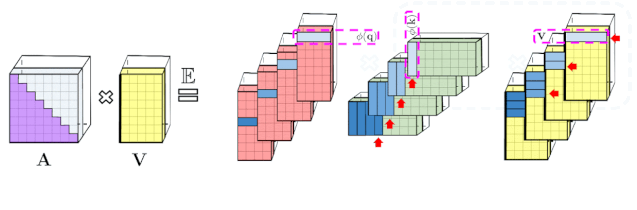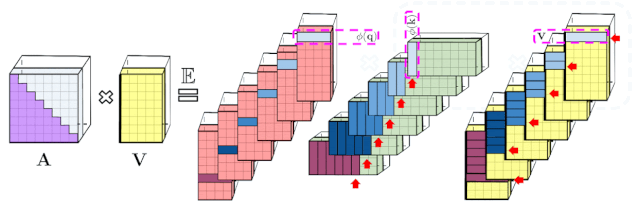
用L表示输入的token序列的长度,常规的点乘注意力就是一个映射,把矩阵 Q , K , V ∈ R L × d Q,K,V∈R^{L×d} Q,K,V∈RL×d作为输入,其中d代表的是隐含维度。矩阵Q,K,V是输入的中间表示,他们的行分别表示为连续字典数据结构的queries,keys,values。双向的点乘注意力有如下的形式,其中 A ∈ R L × L A∈R^{L×L} A∈RL×L 叫做注意力矩阵:
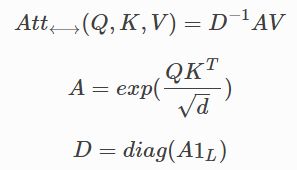
其中这里的 e x p ( ⋅ ) exp(⋅) exp(⋅) 是元素级别的, 1 L 1_L 1L 是长度为L的全1向量, d i a g ( ⋅ ) diag(⋅) diag(⋅) 是对角矩阵。时间复杂度为 O ( L 2 d ) O(L^2d) O(L2d),空间复杂度为 O ( L 2 + L d ) O(L^2+Ld) O(L2+Ld),因为 A A A 需要显式的存储。原则上,点乘注意力的类型和端到端的长序列处理是不相容的。在Seq2Seq结构的encoder自注意力和encoder-decoder注意力应用的是双向注意力。
另一种重要的注意力类型是无向点积注意力有着如下的形式:
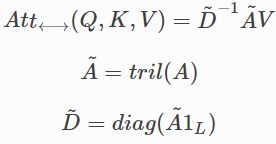
其中 t r i l ( ⋅ ) tril(⋅) tril(⋅)返回参数矩阵的下三角部分,包括对角线。无向的注意力用于自回归生成式模型,例如生成式Transformers中的自注意力,和Seq2Seq Transformers中的decoder部分。
模型改进
广义注意力
在以往的注意力机制中,分别对应矩阵行与列的 query 和 key 输入相乘,通过 softmax 计算形成一个注意力矩阵,以存储相似度系数。值得注意的是,这种方法不能将 query-key 生成结果传递给非线性 softmax 计算之后,再将其分解为原始的 query 和 key。然而,将注意力矩阵分解为原始 query 和 key 的随机非线性函数的乘积是可以的,即所谓的随机特征(random feature),这样就可以更加高效地对相似度信息进行编码。
常规的 softmax 注意力可以看作是由指数函数和高斯投影定义的非线性函数的一个特例。在这里我们也可以反向推理,首先实现一些更广义的非线性函数,隐式定义 query-key 结果中其他类型的相似性度量或核函数。研究者基于早期的核方法(kernel method),将其定义为广义注意力(generalized attention)。尽管对于大多核函数来说,闭式解并不存在,但这一机制仍然可以应用,因为它并不依赖于闭式解。
FAVOR+:通过矩阵相关性实现快速注意力
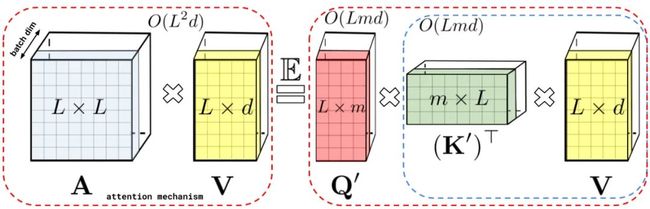
上文描述的分解允许我们以线性而非二次内存复杂度的方式存储隐式注意力矩阵。我们还可以通过分解获得一个线性时间注意力机制。虽然在分解注意力矩阵之后,原始注意力机制与具有值输入的存储注意力矩阵相乘以获得最终结果,我们可以重新排列矩阵乘法以近似常规注意力机制的结果,并且不需要显式地构建二次方大小的注意力矩阵。最终生成了新算法 FAVOR+。
1、FAVOR+理论
FAVOR+使用矩阵 A ∈ R L × L , A ( i , j ) = K ( q i T , k j T ) A∈R^{L×L},A(i,j)=K(q^T_i,k^T_j) A∈RL×L,A(i,j)=K(qiT,kjT),其中 q i / k j q_i/k_j qi/kj代表的是Q/K中第ith/jth 的query/key 行向量,核K: d d × d d → R + d^d×d^d→R_+ dd×dd→R+ 定义为映射ϕ: R d → R + r R^d→R^r_+ Rd→R+r,公式为:
![]()
我们把 ϕ ( u ) ϕ(u) ϕ(u)认为是一个随机特征图(random feature map),其中 u ∈ R d u∈R^d u∈Rd。 Q ′ , K ′ ∈ R L × r Q^′,K^′∈R^{L×r} Q′,K′∈RL×r,行分别用 ϕ ( q i T ) T ϕ(q^T_i)^T ϕ(qiT)T和 ϕ ( k i T ) T ϕ(k^T_i)^T ϕ(kiT)T表示,上述核函数直接促成了高效注意力机制:

A t t ⟷ ⏞ \overbrace{Att⟷} Att⟷ 表示的是近似注意力,括号表示的是计算的顺序。很容易得到这个机制的空间复杂度为 O ( L r + L d + r d ) O(Lr+Ld+rd) O(Lr+Ld+rd),时间复杂度为 O ( L r d ) O(Lrd) O(Lrd),而常规的注意力机制的空间复杂度为 O ( L 2 + L d ) O(L^2+Ld) O(L2+Ld),时间复杂度为 O ( L 2 d ) O(L^2d) O(L2d)。
2、双向注意力近似
3、单向注意力近似
上述分析与双向注意力(即非因果注意力)相关,其中没有过去和未来的概念。对于输入序列中没有注意前后 token 的单向(即因果)注意力而言,研究者稍微修改方法以使用前缀和计算(prefix-sum computation),它们只存储矩阵计算的运行总数,而不存储显式的下三角常规注意力矩阵。
4、softmax-kernels近似softmax
把ϕ用下面的形式表示,函数为 f 1 , . . . f l : R → R f1,...fl:R→R f1,...fl:R→R, 函数 g : R d → R g:R^d→R g:Rd→R和
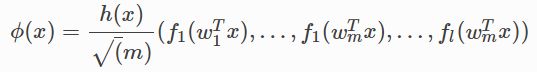
这可以对大多数的核方法进行建模。大多数情况下,D各向同性的,通常是高斯分布。例如:
就变成了高斯核 Kgauss。常规的注意力矩阵的softmax-kernel如下:
不失一般性,省去了 d \sqrt d d,因为我们可以对keys核queries进行规范化。
通过使用三角函数,我们得到了SM(x,y)随机特征图无偏近似:
我们把它叫做 S M ^ m t r i g ( x , y ) \hat{SM} ^{trig}_m(x,y) SM^mtrig(x,y),后面还有一堆理论的分析,有兴趣的可以翻翻论文。
5、正交随机特征(ORF)
上面的部分组成了FAVOR+的R+部分,还差O部分要解释。为了进一步减少估计的反差,我们引入了不通的随机样本w1,…,wm是正交的(orthogonal)。ORF是一个众所周知的方法,但事实证明它是有效的,特别是我们为softmax引入的PRF,我们的第一个理论实验结果表明ORFs可以应用于任何维数d的softmax/高斯核估计的方差的降低,而不仅仅是对足够大的d的渐近估计,这导致了大偏差上的第一个指数小界限严格小于非正交方法的概率。随机特征的正性在这些界限中起着关键作用。
模型参考
论文地址:https://arxiv.org/abs/2009.14794
代码地址:https://github.com/google-research/google-research