滑动轨迹 曲线 python_无人驾驶路径规划技术-三次样条插值曲线及Python代码实现...

自动驾驶运动规划(Motion Planning)是无人驾驶汽车的核心模块之一，它的主要任务之一就是如何生成舒适的、碰撞避免的行驶路径和舒适的运动速度。生成行驶路径最经典方法之一就是是Sampling-Based Planner算法；基于采样的规划器可以规划出可行的轨迹，但这种轨迹往往是折线，为了保证车辆行驶过程中给乘客良好舒适的体验，需要对规划的轨迹进行平滑。Cubic Spline就是一种常用的插值平滑算法，通过一系列的控制点得到一条连续平滑的轨迹。

1、Cubic Spline曲线定义

假定有以下n+1个节点：

把n+1个节点划分成n个区间：

，Cubic Spline是一个满足以下条件的分段定义曲线：

1）在每个分段区间

上，

是一个三次多项式；

2）

；

3）S(x)、

、

在区间[a, b]上连续，即S(x)曲线是光滑的；

每个分段区间的三次多项式构造形式如下：

n个区间共有n个多项式，每个多项式有

，

，

，

4个未知数，所以整个三次样条曲线(Cubic Spline)共有4n个未知数。要求解4n个未知数，需要构造4n个方程。

2、Cubic Spline曲线求解

已知:

a) n+1个数据点[

,

], i = 0, 1, …, n;

b) 每一分段都是三次多项式函数曲线;

c) 节点达到二阶连续;

d) 左右两端点处特性（自然边界，固定边界，非节点边界）

根据已知点求出每段样条曲线方程中的系数，即可得到曲线方程。

曲线求解过程的推导的过程如下：

1）根据插值和连续性的定义：

其中i = 0, 1, ..., n-1

2）根据微分连续性的定义:

其中i = 0, 1, ..., n-2

3）样条曲线的微分式：

a) 由

可以得到：

b) 令

，由

得到：

c) 由

推出：

由此可得：

d) 由

推出：

设

，则有：

a.

可写为：

推出：

b. 将

，

代入

可得：

c. 将

，

，

代入

可得：

根据上述的公式可以得到4n-2个方程，然而有4n个未知数，所以还需要对边界做些约束，所以需要对两端点

和

的微分加些限制。 选择不是唯一的，3种比较常用的限制如下。

a. 自由边界(Natural)

首尾两端没有受到任何让它们弯曲的力，即

，具体表示为

和

，则要求解的方程组可写为：

b. 固定边界(Clamped)

将上述两个公式代入方程组，新的方程组左侧为：

c.非节点边界(Not-A-Knot)

指定样条曲线的三次微分相等，即：

根据

和

，则上述条件变为：

新的方程组系数矩阵可写为：

下图可以看出不同的端点边界对样条曲线的影响：

3、算法总结

假设有n+1个数据节点：

，曲线插值的步骤如下：

a) 计算步长：

，其中i = 0, 1, ..., n-1;

b) 将数据节点和指定的首尾断点条件代入矩阵方程；

c) 解矩阵方程，求得二次微分方程

，该矩阵为三对角矩阵；常见解法为高斯消元法，可以对系数矩阵进行LU分解，分解为单位下三角矩阵和上三角矩阵。即：

d) 计算样条曲线的系数：

其中i=0，1，...，n-1

e. 在每个子区间

中，创建方程：

4、举例

以y=sin(x)为例, x步长为1，x取值范围是[0,10]。对它使用三次样条插值，插值前后对比如下：

5、Python代码实现

三阶样条曲线拟合代码如下：

#! /usr/bin/python

# -*- coding: utf-8 -*-

u"""

Cubic Spline library

author Atsushi Sakai

license: MIT

"""

import math

import numpy as np

class Spline:

u"""

Cubic Spline class

usage:

spline=Spline(x,y)

rx=np.arange(0,4,0.1)

ry=[spline.calc(i) for i in rx]

"""

def __init__(self, x, y):

self.b, self.c, self.d, self.w = [], [], [], []

self.x = x

self.y = y

self.nx = len(x) # dimension of x

h = np.diff(x)

# calc coefficient c

self.a = [iy for iy in y]

# calc coefficient c

A = self.__calc__A(h)

B = self.__calc__B(h)

self.c = np.linalg.solve(A, B)

# print(self.c1)

# calc spline coefficient b and d

for i in range(self.nx - 1):

self.d.append((self.c[i + 1] - self.c[i]) / (3.0 * h[i]))

tb = (self.a[i + 1] - self.a[i]) / h[i] - h[i] * (self.c[i + 1] + 2.0 * self.c[i]) / 3.0

self.b.append(tb)

def calc(self, t):

u"""

Calc position

if t is outside of the input x, return None

"""

if t < self.x[0]:

return None

elif t > self.x[-1]:

return None

i = self.__search_index(t)

dx = t - self.x[i]

result = self.a[i] + self.b[i] * dx + self.c[i] * dx ** 2.0 + self.d[i] * dx ** 3.0

return result

def __search_index(self, x):

u"""

search data segment index

"""

for i in range(self.nx):

if self.x[i] - x > 0:

return i - 1

def __calc__A(self, h):

u"""

calc matrix A for spline coefficient c

"""

A = np.zeros((self.nx, self.nx))

A[0, 0] = 1.0

for i in range(self.nx - 1):

if i is not self.nx - 2:

A[i + 1, i + 1] = 2.0 * (h[i] + h[i + 1])

A[i + 1, i] = h[i]

A[i, i + 1] = h[i]

A[0, 1] = 0.0

A[self.nx - 1, self.nx - 2] = 0.0

A[self.nx - 1, self.nx - 1] = 1.0

return A

def __calc__B(self, h):

u"""

calc matrix B for spline coefficient c

"""

B = np.zeros(self.nx)

for i in range(self.nx - 2):

B[i + 1] = 3.0 * (self.a[i + 2] - self.a[i + 1]) / h[i + 1] - 3.0 * (self.a[i + 1] - self.a[i]) / h[i]

return B

使用上述代码将点集拟合成曲线：

def test1():

import matplotlib.pyplot as plt

# input

x = [-2.5, 0.0, 2.5, 5.0, 7.5]

y = [0.7, -6, 5, 6.5, 0.0]

# 3d spline interporation

spline = Spline(x, y)

rx = np.arange(-2.5, 7.5, 0.01)

ry = [spline.calc(i) for i in rx]

plt.plot(x, y, "xb")

plt.plot(rx, ry, "-r")

plt.grid(True)

plt.axis("equal")

plt.show()

if __name__ == '__main__':

test1()

拟合效果如下：

注：本文首发于微信公众号，转载请注明出处，谢谢！公众号:半杯茶的小酒杯

个人博客地址:http://www.banbeichadexiaojiubei.com​www.banbeichadexiaojiubei.com

参考链接

如需代码请到公众号:【半杯茶的小酒杯】回复"Cubic-Spline-Python20200127"获取。

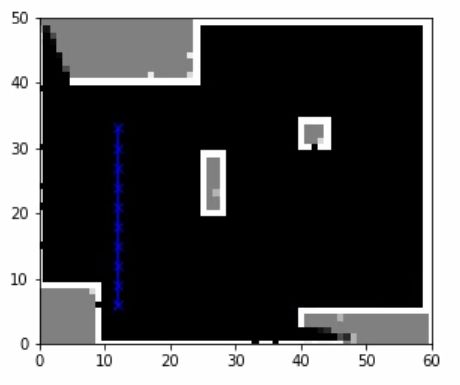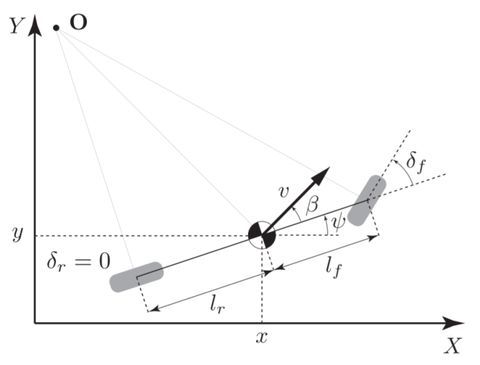相关文章半杯茶的小酒杯：未知环境下的Lidar概率占位栅格图(Occupancy Grid Map) Python代码实现​zhuanlan.zhihu.com半杯茶的小酒杯：自动驾驶Mapping-占位栅格图(Occupancy Grid Map)​zhuanlan.zhihu.com半杯茶的小酒杯：自动驾驶中的车辆运动学模型​zhuanlan.zhihu.com半杯茶的小酒杯：自动驾驶定位算法(十五)基于多传感器融合的状态估计(muti-Sensors Fusion)​zhuanlan.zhihu.com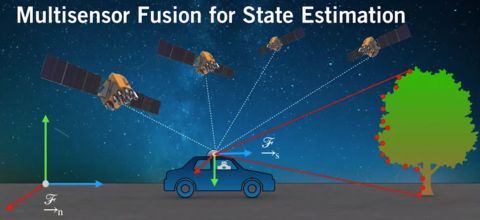自动驾驶路径规划器-Lattice Planner详解​www.banbeichadexiaojiubei.com半杯茶的小酒杯：自动驾驶定位算法(十四)-递归贝叶斯滤波(Bayes Filter)​zhuanlan.zhihu.com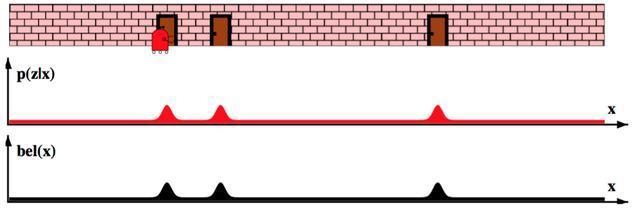半杯茶的小酒杯：自动驾驶定位算法(十三)-粒子滤波(Particle Filter)​zhuanlan.zhihu.com半杯茶的小酒杯：自动驾驶硬件系统(十二)-激光雷达(Lidar)测量模型​zhuanlan.zhihu.com半杯茶的小酒杯：自动驾驶硬件(十一)-Global Navigation Satellite System-GNSS​zhuanlan.zhihu.com自动驾驶定位算法(九)-直方图滤波(Histogram Filter)定位​www.banbeichadexiaojiubei.com