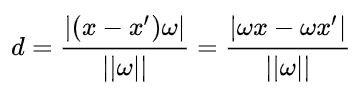对于SVM的一些理解(未更完)

保护罩(就你还想破我防?)

        这篇文章也是我的第一篇博客,类似于学习笔记,全篇都是作者的胡言乱语,不可多多参考,请理性判断,然后还有就是这些里面内容我也是学习了许多优秀的文章,总结了一下大致写出了这篇博客,本人也才是一个"臭大三"的本科普通学生,如有学术出路,还望大家进行指正.

关于SVM

        初次了解,是在一堂午后的课堂,经过了90分钟的学术风暴,让我深知我啥也没懂(老师讲的很好,我不懂主要是上课走神),所以开始了独自探寻SVM真面目的路途.

        首先SVM(支持向量机),是一种二分类模型,其基本模型可以定义为在特征空间(样本点)上间隔最大的线性分类器,其学习目标就是让这个间隔最大化(样本点到决策面的距离),最终转化为一个凸二次规划问题.等价于正则化的合页(hinge)损失函数的最小化问题.

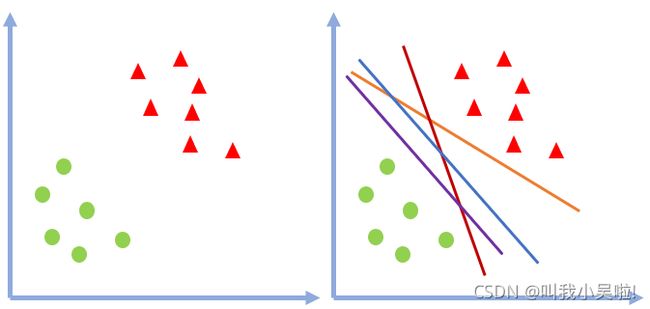
        听起来有点抽象哈,确实,举个栗子,在一个二维空间中,我们仅有两类样本的分类问题,假设我们给定如左图数据集(正样本集和负样本集),我们的任务,把圈圈村和三角村中间找到一跳高速公路(直线的),将两个村落群体分开,只是单纯的分开的话,很简单呀,中间那么大块区域,我随便画画不就分开了吗?,但是如过像紫色那条高速公路话,那三角村民就不乐意了呀,你为啥这么偏袒圈圈村人,而如果画的像红色和橙色那样的路话,可能会引起村内人员的矛盾,比如三角村东边的人为啥比西边的人距离更近,直接掀起内部农民起义了!!,所以这个时候,调解员SVM来了,画出了蓝色这条高速公路,虽然大家可能没有像以前那样被偏袒或者被孤立,但是总体来说对大家都比较公平,便没有在议论了,后来呀,这条蓝色的高速公路被叫做了超平面(多维就变成面啦)

        当然,上述问题也只是建立在二分类,且样本数据已知的时候,我们能比较轻松的去找到这条线,或者超平面,但是一旦样本的维度大于三维的话，我们就没办法把这些样本像上面的图一样画出来了，这时候就看不到了，这时候靠人的双眼也无能为力了,但是计算机是如何找到这条线的呢?SVM调解员为啥能解决村民矛盾纠纷了,那我们就继续向SVM内部去探索

第一关:间隔你为啥又大又小?

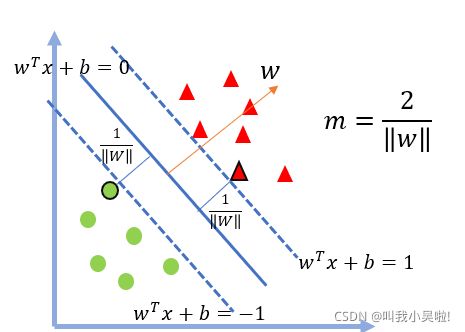
        其实刚刚去解决两个村子的高速公路分配的问题就已经是SVM的思想所在了,可以说是:SVM需要去找一个超平面样本进行分割,而分割的依据就是需要保持对所有的样本"公平",而这种"公平"数学化来说就是去找到所有样本距离到超平面的最小值,但是后面的学习目标是去寻找最大间隔是什么意思呢,我刚刚不才说找最小吗???,其实这个最大的间隔指的是我们一边保持"公平"的同时,去寻找这个中间的区域的最大值(先当于m的值,也是两条虚线之间的距离),相当于置信度,就这个间隔越大,代表我们将数据分的越开,也就越好,所以为了提高我们分类的准确度,所以需要将这个距离尽量的变大.

        而我们这个间隔又是由什么决定的呢?可以看到在我们两条虚直线上有两个黑色边框的圈圈人和三角人,这在我们SVM中就是最有名的VIP客户,因为他们是距离超平面最近的位用户,同时还有一个大气的名字,就叫做支持向量,SVM一方面说是要让大家互相公平,服务于大家,但是最终还是故意偏袒VIP用户(支持向量),让他们两家的一方面保持着与超平面是最小的距离(双方都是最小,不能一边很小,一边很大),又让他们两个之间尽量的离远保持最大的个人空间,这便是间隔一会最大一会最小的原因啦.

        

第二关:数学相关公式的推导过程

         现在我们用数学的语言解释一下, 如上图所示SVM本质是一个判定模型,公式为:

       假设我们有N个训练样本{(x1, y1),(x2, y2), …, (xN, yN)}，x是d维向量，而yi∊{+1, -1}是样本的标签，分别代表两个不同的类。当f(xi)>0时yi=1,当f(xi)<0时,yi=-1可以写做:

         上面的式子最终等价于yi(w*x+b)>0,而当超平面确定之后,对于最大间隔,可以根据我们以前学的平面知识,去求出每个点到直线的距离,将这个表达为distance,有N个样本点i就代表有N个distance,去找到最小的distance,就等于margin了

         可能在这里基础不好的同学可能就会疑惑了,这里的distance为什么要这么写,还有啥是范数呀,可以像番薯一样可以吃吗?,其实这里的范数其实是二阶范数,  L2范数是指向量各元素的平方和然后求平方根.范数的本质是距离，存在的意义是实现比较。因为向量与矩阵无法像标量直接比较大小，因而通过范数（称为函数或者映射也可以）把不能比较的量转换为可以比较的实数

                                     

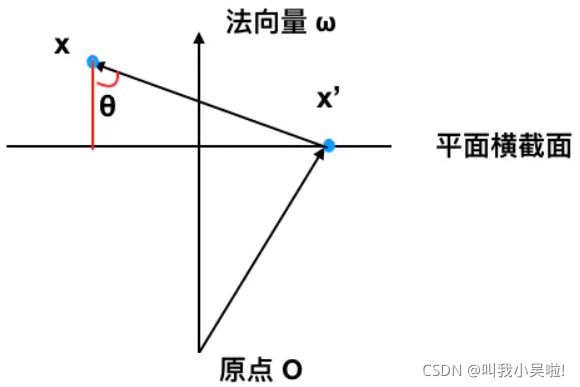
        上图中x是平面外的一点.我们要求的距离记为d,也就是红色的线段.根据三角函数可以得到：

                                                             

        （空间中一点向超平面作垂线，只能是锐角，不必担心正负）.又因为d肯定和法向量平行，所以这样来算夹角：（因为法向量可能反向，所以给等式左边加上绝对值）联立得：

 

 又因为x'在超平面内,所以wx' = -b , 于是最后得到了任意点到超平面的距离公式为:

   然后通过上面的方法我们解决了距离公式的来源,那么继续往下走.后续知识以后有时间补上