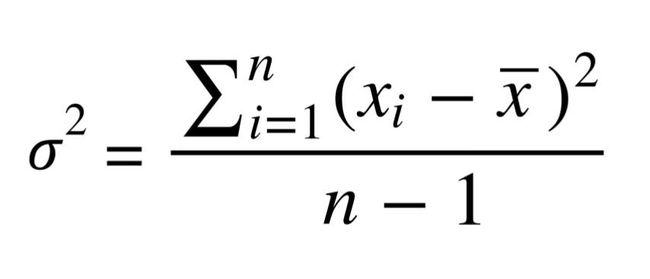python 描述性统计_Python中的基本统计：描述性统计

python 描述性统计

The field of statistics is often misunderstood, but it plays an essential role in our everyday lives. Statistics, done correctly, allows us to extract knowledge from the vague, complex, and difficult real world. Wielded incorrectly, statistics can be used to harm and mislead. A clear understanding of statistics and the meanings of various statistical measures is important to distinguishing between truth and misdirection.

统计领域经常被误解，但在我们的日常生活中起着至关重要的作用。 正确完成的统计数据使我们能够从模糊，复杂和困难的现实世界中提取知识。 错误地使用统计信息可能会造成伤害和误导。 清楚地了解统计数据和各种统计方法的含义对于区分真相和误导很重要。

We will cover the following in this article:

我们将在本文中介绍以下内容：

• defining statistics
• descriptive statistics
  • measures of central tendency
  • measures of spread

• 定义统计
• 描述性统计
  • 集中趋势的量度
  • 传播措施

先决条件： (Prerequisites:)

This article assumes no prior knowledge of statistics, but does require at least a general knowledge of Python. If you are uncomfortable with for loops and lists, I recommend covering them briefly before progressing.

本文假定您没有统计学的先验知识，但至少需要具备Python的一般知识。 如果您对for循环和列表不满意 ，建议您在进行操作之前简要介绍一下它们。

载入我们的数据 (Loading in our data)

We will root our discussion of statistics in real-world data, taken from Kaggle’s Wine Reviews data set. The data itself comes from a scraper that scoured the Wine Enthusiast site.

我们将对统计数据的讨论植根于来自Kaggle的Wine Reviews数据集的真实数据。 数据本身来自刮擦酒爱好者网站的刮板。

For the sake of this article, let’s say that you are a sommelier-in-training, a new wine taster. You found this interesting data set on wines, and you would like to compare and contrast different wines. You’ll use statistics to describe the wines in the data set and derive some insights for yourself. Perhaps we can start our training with a cheap set of wines, or the most highly rated ones?

就本文而言，假设您是一位培训侍酒师，是一名新的葡萄酒品尝师。 您找到了有关葡萄酒的有趣数据集，并且想要比较和对比不同的葡萄酒。 您将使用统计数据来描述数据集中的葡萄酒，并为自己得出一些见解。 也许我们可以从便宜的葡萄酒或评级最高的葡萄酒开始我们的培训？

The code below loads in the data set wine-data.csv into a variable wines as list of lists. We’ll perfrom statistics on wines throughout the article. You can use this code to follow along on your own computer.

下面的代码将数据集wine-data.csv装入列表中的变量wines中。 在整篇文章中，我们将对wines进行统计。 您可以使用此代码在自己的计算机上继续学习。

import csv
with open("wine-data.csv", "r", encoding="latin-1") as f:
    wines = list(csv.reader(f))
import csv
with open("wine-data.csv", "r", encoding="latin-1") as f:
    wines = list(csv.reader(f))
 

Let’s have a brief look at the first five rows of the data in table, so we can see what kinds of values we’re working with.

让我们简要看一下表中数据的前五行，这样我们就可以看到我们正在使用哪种类型的值。

index	指数	country	国家	description	描述	designation	指定	points	点数	price	价钱	province	省	region_1	region_1	region_2	region_2	variety	品种	winery	酒厂
0	0	US	我们	“This tremendous 100%…”	“这真是百分百……”	Martha’s Vineyard	玛莎葡萄园岛	96	96	235	235	California	加利福尼亚州	Napa Valley	纳帕谷	Napa	纳帕	Cabernet Sauvignon	赤霞珠	Heitz	海兹
1	1个	Spain	西班牙	“Ripe aromas of fig…	“无花果的成熟香气……	Carodorum Selecci Especial Reserva	Carodorum Selecci特别储备	96	96	110	110	Northern Spain	西班牙北部	Toro	托罗			Tinta de Toro	Tinta de Toro	Bodega Carmen Rodriguez	Bodega卡门·罗德里格斯（Bodega Carmen Rodriguez）
2	2	US	我们	“Mac Watson honors…	“ Mac Watson荣幸……	Special Selected Late Harvest	特别精选晚收	96	96	90	90	California	加利福尼亚州	Knights Valley	骑士谷	Sonoma	索诺玛	Sauvignon Blanc	长相思	Macauley	麦考利
3	3	US	我们	“This spent 20 months…	“这花了20个月……	Reserve	保留	96	96	65	65	Oregon	俄勒冈州	Willamette Valley	威拉米特山谷	Willamette Valley	威拉米特山谷	Pinot Noir	黑比诺	Ponzi	庞兹
4	4	France	法国	“This is the top wine…	“这是顶级葡萄酒……	La Brelade	拉布雷拉德	95	95	66	66	Provence	普罗旺斯	Bandol	邦多			Provence red blend	普罗旺斯红色混合	Domaine de la Begude	贝古德酒庄

统计到底是什么？ (What precisely is/are statistics?)

This question is deceptively difficult. Statistics is many, many things, so trying to pigeonhole it into a brief summary would undoubtedly obscure some details from us, but we must start somewhere.

这个问题看似困难。 统计数据涉及很多方面，因此尝试将其归纳为简短摘要无疑会掩盖我们的一些细节，但我们必须从某个地方入手。

As an entire field, statistics can be thought of as a scientific framework for handling data. This definition includes all the tasks involved with collecting, analyzing, and interpretation of data. Statistics can also refer to individual measures that represent summaries or aspects of the data itself. Throughout the article, we will do our best to distinguish between the field and the actual measurements.

在整个领域中，统计数据都可以视为处理数据的科学框架 。 该定义包括与数据收集，分析和解释有关的所有任务。 统计信息也可以指代表数据本身摘要或方面的各个度量。 在整篇文章中，我们将尽力区分现场和实际测量。

This natrually leads us to ask: but what is data? Luckily for us, data is simpler to define. Data is a general collection of observations of the world, and can be widely varied in nature, ranging from qualitative to quantitative. Researchers gather data from experiments, entrepeneurs gather data from their users, and game companies gather data on their player behavior.

这自然使我们问：但是什么是数据？ 对我们来说幸运的是，数据更易于定义。 数据是对世界观测资料的一般收集，其性质可以从定性到定量变化很大。 研究人员从实验中收集数据，企业家从用户中收集数据，游戏公司从玩家行为中收集数据。

These examples point out another important facet of data: observations usually pertain to a population of interest. Referring back to a previous example, a researcher may be looking at a group of patients with a particular condition. For our data, the population in question is a a set of wine reviews. The term population is pointedly vague. By clearly defining our population, we are able to perform statistics on our data and extract knowledge from them.

这些例子指出了数据的另一个重要方面：观察通常涉及感兴趣的人群 。 回到先前的例子，研究人员可能正在看一组患有特定疾病的患者。 对于我们的数据，有问题的人口是一组葡萄酒评论。 人口一词是含糊的。 通过清楚地定义我们的人口，我们能够对我们的数据进行统计并从中提取知识。

But why should we be interested in populations? It is useful to be able to compare and contrast populations to test our ideas about the world. We’d like to know that patients receiving a new treatment actually fare better than those receiving a placebo, but we also want to prove this quantitatively. This is where statistics comes in: giving us a rigorous way to approach data and make decisions informed by real events in the world rather than abstract guesses about it.

但是，为什么我们应该对人口感兴趣？ 能够比较和对比人群以测试我们对世界的想法是很有用的。 我们想知道接受新疗法的患者实际上比接受安慰剂的患者好，但是我们也想定量地证明这一点。 这就是统计信息的来源：它为我们提供了一种严谨的方法来处理数据并根据世界上的真实事件做出决策，而不是对数据进行抽象猜测。

关键要点： (Key takeaways:)

• Statistics is the science of data.
• Data is any collection of observations on a population of interest.
• Statistics give us a concrete way to compare populations using numbers rather than ambiguous description.

• 统计是数据科学。
• 数据是对感兴趣人群的任何观察结果的集合。
• 统计数据为我们提供了一种使用数字而不是模棱两可的描述来比较人口的具体方法。

描述性统计 (Descriptive statistics)

When we have a set of observations, it is useful to summarize features of our data into a single statement called a descriptive statistic. As their name suggests, descriptive statistics describe a particular quality of the data they summarize. These statistics fall into two general categories: the measures of central tendency and the measures of spread.

当我们有一组观察结果时，将数据的特征汇总为一个称为描述性统计量的陈述是很有用的。 顾名思义，描述性统计描述了他们汇总的数据的特定质量。 这些统计数据可分为两大类： 集中趋势的度量和传播的度量 。

集中趋势的度量 (Measures of central tendency)

The measures of central tendency are metrics that represent an answer to the following question: “What does the middle of our data look like?” The word middle is vague because there are multiple definitions we can use to represent the middle. We’ll discuss how each new measure changes how we define the middle.

集中趋势的度量是表示以下问题的答案的度量：“我们的数据中间是什么样的？” 中间一词含糊不清，因为我们可以使用多种定义来表示中间。 我们将讨论每个新指标如何改变我们定义中间值的方式。

意思 (Mean)

The mean is a descriptive statistic that looks at the average value of a data set. While mean is the technical word, most people will understand it as just the average.

平均值是一种描述性统计，用于查看数据集的平均值。 虽然“卑鄙”是专业术语，但大多数人只会将其理解为平均值。

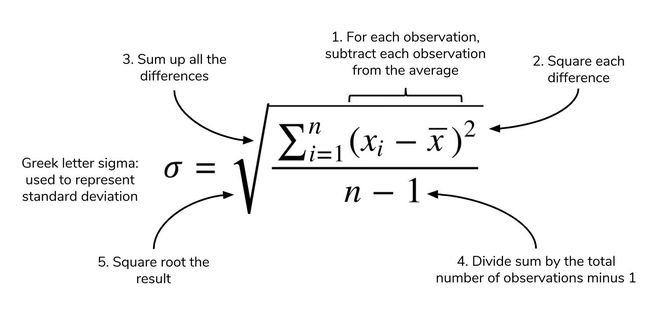
How is this the mean calculated? The picture below takes the actual equation and breaks down the calculation components into simpler terms.

该平均值如何计算？ 下图显示了实际方程式，并将计算成分分解为更简单的术语。

In the case of the mean, the “middle” of the data set refers to this typical value. The mean represents a typical observation in our data set. If we were to pick one of our observations at random, then we’re likely to get a value that’s close to the mean.

在平均值的情况下，数据集的“中间”是指该典型值。 平均值代表我们数据集中的典型观察结果。 如果我们随机选择一个观察值，那么我们很可能会获得接近均值的值。

The calculation of the mean is a simple task in Python. Let’s figure out what the average wine score in the data set is.

平均值的计算是Python中的一项简单任务。 让我们弄清楚数据集中的平均葡萄酒得分是多少。

The average score in the wine data set tells us that the “typical” score in the data set is around 87.8. This tells us that most wines in the data set are highly rated, assuming that a scale of 0 to 100. However, we must take note that the Wine Enthusiast site chooses not to post reviews where the score is below 80.

葡萄酒数据集中的平均得分告诉我们，数据集中的“典型”得分约为87.8。 这告诉我们，数据集中大多数葡萄酒的评分都很高，假设评分范围为0到100。但是，我们必须注意，Wine Enthusiast网站选择不对分数低于80的人发表评论。

There are multiple types of means, but the this form is the most common use. This mean is referred to as the arithmetic mean since we are summing up the values of interest.

手段有多种类型，但是这种形式是最常见的用法。 该均值称为算术均值，因为我们正在对感兴趣的值求和。

中位数 (Median)

The next measure of central tendency we’ll cover is the median. The median also attempts to define a typical value in the data set, but unlike mean, does not require calculation.

我们将涵盖的下一个集中趋势的度量是中位数 。 中位数也试图在数据集中定义一个典型值，但与平均值不同，它不需要计算。

To find the median, we first need to reorganize our data set in ascending order. Then the median is the value that coincides with the middle of the data set. If there are an even amount of items, then we take the average of the two values that would “surround” the middle.

要找到中位数，我们首先需要按升序重组数据集。 然后，中位数是与数据集的中间部分重合的值。 如果有偶数个项目，则我们取两个值的平均值作为“中间”值。

While Python’s standard library does not support a median function, we can still find the median using the process we’ve described. Let’s try to find the median value of the wine prices.

尽管Python的标准库不支持中位数函数，但我们仍然可以使用我们描述的过程来找到中位数。 让我们尝试找到葡萄酒价格的中位数。

# Isolate prices from the data set
prices = [float(w[5]) for w in wines if w[5] != ""]

# Find the number of wine prices 
num_wines = len(prices)

# We'll sort the wine prices into ascending order
sorted_prices = sorted(prices)

# We'll calculate the middle index 
middle = (num_wines / 2) + 0.5

# Now we can return the median
sorted_prices[middle]
>>> 24
# Isolate prices from the data set
prices = [float(w[5]) for w in wines if w[5] != ""]

# Find the number of wine prices 
num_wines = len(prices)

# We'll sort the wine prices into ascending order
sorted_prices = sorted(prices)

# We'll calculate the middle index 
middle = (num_wines / 2) + 0.5

# Now we can return the median
sorted_prices[middle]
>>> 24
 

The median price of a wine bottle in the data set is $24. This finding suggests that at least half of the wines in the data set are sold for $24 or less. That’s pretty good! What if we tried to find the mean? Given that they both represent a typical value, we would expect that they would be around the same.

数据集中的葡萄酒瓶中位数价格为24美元。 这一发现表明，数据集中至少有一半的葡萄酒售价为24美元或更低。 很好！ 如果我们试图找到均值怎么办？ 考虑到它们都代表一个典型值，我们希望它们大致相同。

An average price of $33.13 is certainly far off from our median price, so what happened here? The difference between mean and median is due to robustness.

33.13美元的平ASP格肯定与我们的中位数价格相去甚远，那么这里发生了什么？ 均值和中位数之间的差异是由于健壮性 。

离群值问题 (The problem of outliers)

Remember that the mean is calculated by summing up all the values we want and dividing by the number of items, while the median is found by simply rearranging items. If we have outliers in our data, items that are much higher or lower than the other values, it can have an adverse effect on the mean. That is to say, the mean is not robust to outliers. The median, not having to look at outliers, is robust to them.

请记住，均值是通过将我们想要的所有值相加并除以项目数而得出的，而中位数则是通过简单地重新排列项目而得出的。 如果我们的数据中有离群值 ，即项目比其他值高或低很多，则可能对均值产生不利影响。 也就是说，均值对离群值不具有鲁棒性 。 中位数无需关注异常值，因此对它们具有鲁棒性。

Let’s have a look at the maximum and minimum prices that we see in our data.

让我们看一下我们在数据中看到的最高和最低价格。

min_price = min(prices)
max_price = max(prices)
print(min_price, max_price)
4.0, 2300.0
min_price = min(prices)
max_price = max(prices)
print(min_price, max_price)
4.0, 2300.0
 

We now know that outliers are present in our data. Outliers can represent interesting events or errors in our data collection, so it’s important to be able to recognize when they’re present in the data. The comparison of median and mode is just one of many ways to detect the presence of outliers, though visualization is usually a quicker way to detect them.

现在我们知道数据中存在异常值。 离群值可以代表我们数据收集中的有趣事件或错误，因此能够识别数据中何时存在异常值非常重要。 中位数和众数的比较只是检测异常值的许多方法之一，尽管可视化通常是检测异常值的较快方法。

模式 (Mode)

The last measure of central tendency that we’ll discuss is the mode. The mode is defined as the value that appears the most frequently in our data. The intuition of the mode as the “middle” is not as immediate as mean or median, but there is a clear rationale. If a value appears repeatedly throughout the data, we also know it will influence the average towards the modal value. The more a value appears, the more it will influence the mean. Thus, a mode represents the highest weighted contributing factor to our mean.

我们将讨论的集中趋势的最后一个量度是模式 。 模式定义为在我们的数据中最频繁出现的值。 模式作为“中间”的直觉不如均值或中间值那么直接，但是有一个明确的理由。 如果一个值在整个数据中反复出现，我们也知道它将影响平均值对模态值的影响。 值显示的越多，对平均值的影响就越大。 因此，模式代表了我们平均值的最高加权贡献因子。

Like median, there is no built-in mode function in Python, but we can figure it out by counting the appearance of our prices and looking for the max.

像中位数一样，Python中没有内置模式函数，但是我们可以通过计算价格外观并寻找最大值来找出它。

The mode is reasonably close to the median, so we can have a measure of confidence that we both the median and mode represent the middle values of our wine prices.

该模式相当接近中位数，因此我们可以对中位数和模式都表示葡萄酒价格的中间值有一定的信心。

The measures of central tendency are useful for summarizing what an average observation is like in our data. However, they do not inform us as to how spread out are data is. These summaries of spread are what the measures of spread help describe.

集中趋势的度量对于总结我们的数据中的平均观察值很有用。 然而，他们没有告诉我们摊开如何数据。 这些传播摘要是对传播手段的描述。

传播措施 (Measures of spread)

The measures of spread (also known as dispersion) answer the question, “How much does my data vary?” There are few things in the world that stay the same everytime we observe it. We all know someone who has lamented a slight change in body weight that is due to natural fluctuation rather than outright weight gain. This variability makes the world fuzzy and uncertain, so it’s useful to have metrics that summarize this “fuzziness.”

传播量度（也称为分散度）回答了以下问题：“我的数据有多少变化？” 每次我们观察时，世界上很少有事物保持不变。 我们都知道有人对体重的轻微变化感到遗憾，这是由于自然的波动而不是完全的体重增加。 这种可变性使整个世界变得模糊而不确定，因此，具有用于总结这种“模糊性”的指标非常有用。

范围和四分位数范围 (Range and interquartile range)

The first measure of spread we’ll cover is range. Range is the simplest to compute of the measures we’ll see: just subtract the smallest value of your data set from the largest value in the data.

我们要覆盖的第一个价差是范围 。 范围是我们将要看到的度量的最简单计算方法：只需从数据中的最大值减去数据集的最小值即可。

We found out what the minimum and maximum values of our wine prices were when we were investigating the median, so we’ll use these to find the range.

在调查中位数时，我们发现了我们的葡萄酒价格的最小和最大值是多少，因此我们将使用这些来找到范围。

price_range = max_price - min_price
print(price_range)
>>> 2296.0
price_range = max_price - min_price
print(price_range)
>>> 2296.0
 

We found a range of 2296, but what does that mean precisely? When we look at our various measures, it is important to keep all of this information in the context of your data. Our median price was $24, and our range is $2296. The range is two orders of magnitude higher than our median, so it suggests that our data is extremely spread out. Perhaps if we had another wine data set, we could compare the ranges of these two data sets to gain an understanding on how they differ. Otherwise, the range alone isn’t super helpful.

我们找到了2296的范围，但这究竟意味着什么？ 当我们查看各种度量时，将所有这些信息保留在您的数据上下文中非常重要。 我们的中位数价格为24美元，我们的价格区间为2296美元。 该范围比我们的中位数高两个数量级，因此表明我们的数据非常分散。 也许如果我们有另一个葡萄酒数据集，我们可以比较这两个数据集的范围，以了解它们之间的区别。 否则，仅靠范围并不是超级有帮助。

More often, we’ll want to see how much our data varies from the typical value. This summary falls under the jurisdiction of standard deviation and variance.

更常见的是，我们希望查看我们的数据与典型值之间的差异。 本摘要属于标准偏差和方差的管辖范围。

标准偏差 (Standard deviation)

The standard deviation is also a measure of the spread of your observations, but is a statement of how much your data deviates from a typical data point. That is to say, the standard deviation summarizes how much your data differs from the mean. This relationship to the mean is apparent in standard deviation’s calculation.

标准偏差还可以衡量观察值的范围，但是可以说明您的数据偏离典型数据点的程度。 也就是说，标准差汇总了您的数据与平均值之间的差异。 与平均值的关系在标准偏差的计算中很明显。

The structure of the equation merits some discussion. Recall that the mean is calculated by summing up all of your observations and dividing it by the number of observations. The standard deviation equation is similar but seeks to calculate the average deviation from the mean, in addition to an extra square root operation.

该方程的结构值得讨论。 回想一下，均值是通过对所有观察值求和并除以观察数而得出的。 标准偏差方程式类似，但是除额外的平方根运算外，还试图计算与平均值的平均偏差。

You may see elsewhere that n is the denominator instead of n-1. The specifics of this details is outside the scope of this article, but know that using n-1 is generally considered to be more correct. A link to an explanation is at the end of this article.

您可能在其他地方看到n是分母而不是n-1 。 这些详细信息的细节不在本文讨论范围之内，但是知道使用n-1通常被认为是更正确的。 指向说明的链接位于本文的末尾。

We’d like to calculate the standard deviation to better characterize our wine prices and scores, so we’ll create a dedicated function for this. Calculating a cumulative sum of numbers is cumbersome by hand, but Python’s for loops make this trivial. We are making our own function to demonstrate that Python makes it easy to perform these statistics, but it’s also good to know that the numpy library also implements standard deviation under std.

我们想计算标准偏差，以更好地表征我们的葡萄酒价格和分数，因此我们将为此创建专用功能。 手工计算数字的累加总会很麻烦，但是Python的for循环使这个琐碎的事变得微不足道。 我们正在使用自己的函数来证明Python使执行这些统计信息变得容易，但是也很高兴知道numpy库还在std下实现了标准差。

These results are expected. The scores only range from 80 to 100, so we know that the standard deviation would be small. In contrast, the prices with its outliers produces a much higher value. The larger the standard deviation, the more spread out the data is around the mean and vice-versa.

这些结果是预期的。 分数仅在80到100之间，因此我们知道标准偏差会很小。 相反，价格及其离群值产生了更高的价值。 标准偏差越大，数据在均值附近分布越多，反之亦然。

We will see that variance is closely related to standard deviation.

我们将看到方差与标准差密切相关。

方差 (Variance)

Often, standard deviation and variance are lumped together for good reason. The following is the equation for variance, does it look familiar?

通常，有充分的理由将标准偏差和方差汇总在一起。 以下是方差方程，它看起来很熟悉吗？

Variance and standard deviation are almost the exact same thing! Variance is just the square of the standard deviation. Likewise, variance and standard deviation represent the same thing — a measure of spread — but it’s worth noting that the units are different. Whatever units your data are in, standard deviation will be the same, and variation will be in that units-squared.

方差和标准偏差几乎完全相同！ 方差只是标准偏差的平方。 同样，方差和标准偏差代表同一件事-衡量价差-但值得注意的是单位不同。 无论数据以什么单位表示，标准偏差都将相同，并且变化将以该单位平方为单位。

A question that many statistics starters ask is, “But why do we square the deviation? Won’t the absolute value get rid of pesky negatives in the sum?” While avoiding negative values in the sum is a reason for the squaring operation, it’s not the only one. Like the mean, variance and standard deviation are affected by outliers. Many times, outliers are also points of interest in our data set, so squaring the difference from the mean allows us to point out this significance. If your are familiar with calculus, you’ll see that having an exponential term allows us to find our where the point of minimum deviation is.

许多统计初学者提出的问题是：“但是为什么要对偏差平方呢？ 绝对值是否会消除总和中令人讨厌的负数？” 虽然避免求和为负值是进行平方运算的原因，但不是唯一的原因。 像平均值一样，方差和标准偏差也受异常值的影响。 很多时候，离群值也是我们数据集中的关注点，因此，将差值与均值平方可以使我们指出这一意义。 如果您熟悉微积分，您会发现拥有指数项使我们能够找到最小偏差点所在的位置。

More often than not, any statistical analyses you do will require just the mean and standard deviation, but the variance still has significance in other academic areas. The measures of central tendency and spread allow us to summarize key aspects of our data set, and we can build on these summaries to glean more insights from our data.

通常，您所做的任何统计分析都只需要均值和标准差，但是方差在其他学术领域仍然具有重要意义。 集中趋势和分布的度量使我们能够总结数据集的关键方面，并且我们可以基于这些摘要来从数据中收集更多的见解。

重要要点 (Key takeaways)

• Descriptive statistics provide simple summaries of our data.
• The (arithmetic) mean calculates the typical value of our data set. It is not robust.
• The median is the exact middle value of our data set. It is robust.
• The mode is the value that appears the most.
• The range is the difference between the largest and smallest value in our data set.
• The variance and standard deviation are the average distance from the mean.

• 描述性统计信息提供了我们数据的简单汇总。
• （算术）平均值计算我们数据集的典型值。 它并不健壮。
• 中位数是我们数据集的确切中间值。 它很健壮。
• 模式是最出现的值。
• 范围是我们数据集中最大值和最小值之间的差。
• 方差和标准偏差是与平均值的平均距离。

结论 (Conclusion)

It’s easy to get mired in the equations and details of statistical equations, but it’s important to understand what these concepts represent. In this article, we explored some of the details behind some basic descriptive statistics, while looking at some wine data to ground our concepts.

容易陷入方程式和统计方程式的细节中，但是了解这些概念的含义很重要。 在本文中，我们研究了一些基本描述性统计数据背后的一些细节，同时查看了一些葡萄酒数据以奠定我们的概念基础。

In the next part, we’ll discuss the relationship between statistics and probability. The descriptive statistics we learned here play a key role in understanding this connection, so it’s important to remember what these concepts represent before moving foward.

在下一部分中，我们将讨论统计量和概率之间的关系。 我们在这里学习到的描述性统计数据在理解这种联系方面起着关键作用，因此在继续前进之前记住这些概念代表什么很重要。

进一步阅读： (Further Reading:)

Earlier in the article, we glossed over why standard deviation has an n-1 term instead of n. The use of the n-1 term is referred to as *Bessel’s Correction.”

在本文的前面，我们掩盖了为什么标准差使用n-1项而不是n 。 n-1项的使用称为*贝塞尔校正。”

• Bessel’s Correction: Why the denominator of standard devation is n-1

• 贝塞尔的更正：为什么标准偏差的分母为n-1

翻译自: https://www.pybloggers.com/2018/07/basic-statistics-in-python-descriptive-statistics/

python 描述性统计