量子计算解线性方程:HHL algorithm for quantum linear equation
Introduction
Systems of linear equations arise naturally in many real-life applications in a wide range of areas, such as in the solution of Partial Differential Equations, the calibration of financial models, fluid simulation or numerical field calculation. The problem can be defined as, given a m a t r i x A ∈ C N × N matrix A\in\mathbb{C}^{N\times N} matrixA∈CN×N and a vector b ⃗ ∈ C N \vec{b}\in\mathbb{C}^{N} b∈CN, find x ⃗ ∈ C N \vec{x}\in\mathbb{C}^{N} x∈CN satisfying A x ⃗ = b ⃗ A\vec{x}=\vec{b} Ax=b
For example, take N=2,
A = ( 1 − 1 / 3 − 1 / 3 1 ) , x ⃗ = ( x 1 x 2 ) and b ⃗ = ( 1 0 ) A = \begin{pmatrix}1 & -1/3\\-1/3 & 1 \end{pmatrix},\quad \vec{x}=\begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix}\quad \text{and} \quad \vec{b}=\begin{pmatrix}1 \\ 0\end{pmatrix} A=(1−1/3−1/31),x=(x1x2)andb=(10)
Then the problem can also be written as find x 1 , x 2 ∈ C s u c h t h a t { x 1 − x 2 3 = 1 − x 1 3 + x 2 = 0 x_{1}, x_{2}\in\mathbb{C} such that \begin{cases}x_{1} - \frac{x_{2}}{3} = 1 \\ -\frac{x_{1}}{3} + x_{2} = 0\end{cases} x1,x2∈Csuchthat{x1−3x2=1−3x1+x2=0
A system of linear equations is called s-sparse if A has at most s non-zero entries per row or column. Solving an s-sparse system of size N with a classical computer requires O ( N s κ log ( 1 / ϵ ) ) \mathcal{ O }(Ns\kappa\log(1/\epsilon)) O(Nsκlog(1/ϵ)) running time using the conjugate gradient method. Here κ \kappa κ denotes the condition number of the system and ϵ \epsilon ϵ the accuracy of the approximation.
The HHL is a quantum algorithm to estimate a function of the solution with running time complexity of O ( log ( N ) s 2 κ 2 / ϵ ) \mathcal{ O }(\log(N)s^{2}\kappa^{2}/\epsilon) O(log(N)s2κ2/ϵ) when A is a Hermitian matrix under the assumptions of efficient oracles for loading the data, Hamiltonian simulation and computing a function of the solution. This is an exponential speed up in the size of the system, however one crucial remark to keep in mind is that the classical algorithm returns the full solution, while the HHL can only approximate functions of the solution vector.
The HHL algorithm
Some mathematical background
The first step towards solving a system of linear equations with a quantum computer is to encode the problem in the quantum language. By rescaling the system, we can assume b ⃗ \vec{b} b and x ⃗ \vec{x} x to be normalised and map them to the respective quantum states ∣ b ⟩ |b\rangle ∣b⟩ and ∣ x ⟩ |x\rangle ∣x⟩. Usually the mapping used is such that i t h i^{th} ith component of b ⃗ \vec{b} b (resp. x ⃗ ) \vec{x}) x) corresponds to the amplitude of the i t h i^{th} ith basis state of the quantum state ∣ b ⟩ |b\rangle ∣b⟩ (resp. ∣ x ⟩ ) |x\rangle) ∣x⟩). From now on, we will focus on the rescaled problem
A ∣ x ⟩ = ∣ b ⟩ A|x\rangle=|b\rangle A∣x⟩=∣b⟩
Since A is Hermitian, it has a spectral decomposition
A = ∑ j = 0 N − 1 λ j ∣ u j ⟩ ⟨ u j ∣ , λ j ∈ R A=\sum_{j=0}^{N-1}\lambda_{j}|u_{j}\rangle\langle u_{j}|,\quad \lambda_{j}\in\mathbb{ R } A=j=0∑N−1λj∣uj⟩⟨uj∣,λj∈R
where ∣ u j ⟩ i s t h e j t h |u_{j}\rangle is the j^{th} ∣uj⟩isthejth eigenvector of A with respective eigenvalue λ j \lambda_{j} λj. Then,
A − 1 = ∑ j = 0 N − 1 λ j − 1 ∣ u j ⟩ ⟨ u j ∣ A^{-1}=\sum_{j=0}^{N-1}\lambda_{j}^{-1}|u_{j}\rangle\langle u_{j}| A−1=∑j=0N−1λj−1∣uj⟩⟨uj∣
and the right hand side of the system can be written in the eigenbasis of A as
∣ b ⟩ = ∑ j = 0 N − 1 b j ∣ u j ⟩ , b j ∈ C |b\rangle=\sum_{j=0}^{N-1}b_{j}|u_{j}\rangle,\quad b_{j}\in\mathbb{ C } ∣b⟩=j=0∑N−1bj∣uj⟩,bj∈C
It is useful to keep in mind that the goal of the HHL is to exit the algorithm with the readout register in the state
∣ x ⟩ = A − 1 ∣ b ⟩ = ∑ j = 0 N − 1 λ j − 1 b j ∣ u j ⟩ |x\rangle=A^{-1}|b\rangle=\sum_{j=0}^{N-1}\lambda_{j}^{-1}b_{j}|u_{j}\rangle ∣x⟩=A−1∣b⟩=j=0∑N−1λj−1bj∣uj⟩
Note that here we already have an implicit normalisation constant since we are talking about a quantum state.
All we need to find is
Description of the HHL algorithm
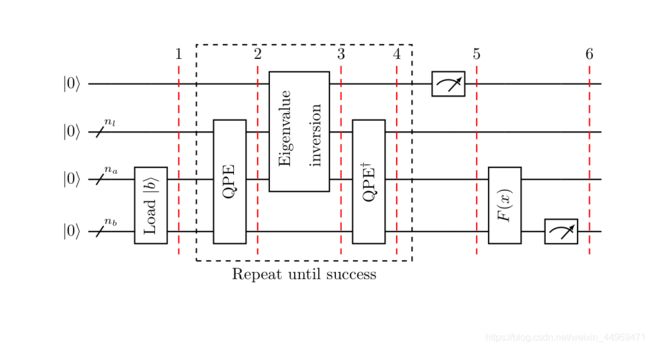
The algorithm uses three quantum registers, all of them set to ∣ 0 ⟩ |0\rangle ∣0⟩ at the beginning of the algorithm. One register, which we will denote with the subindex n l n_{l} nl, is used to store a binary representation of the eigenvalues of A. A second register, denoted by n b n_{b} nb, contains the vector solution, and from now on N = 2 n b N=2^{n_{b}} N=2nb. There is an extra register, for the auxiliary qubits. These are qubits used as intermediate steps in the individual computations but will be ignored in the following description since they are set to ∣ 0 ⟩ |0\rangle ∣0⟩ at the beginning of each computation and restored back to the ∣ 0 ⟩ |0\rangle ∣0⟩ state at the end of the individual operation.
The following is an outline of the HHL algorithm with a high-level drawing of the corresponding circuit. For simplicity all computations are assumed to be exact in the ensuing description, and a more detailed explanation of the non-exact case is given in Section 2.D…
Load the data ∣ b ⟩ ∈ C N |b\rangle\in\mathbb{ C }^{N} ∣b⟩∈CN. That is, perform the transformation
∣ 0 ⟩ n b ↦ ∣ b ⟩ n b |0\rangle _{n_{b}} \mapsto |b\rangle _{n_{b}} ∣0⟩nb↦∣b⟩nb
Apply Quantum Phase Estimation (QPE) with
U = e i A t : = ∑ j = 0 N − 1 e i λ j t ∣ u j ⟩ ⟨ u j ∣ U = e ^ { i A t } := \sum _{j=0}^{N-1}e ^ { i \lambda _ { j } t } |u_{j}\rangle\langle u_{j}| U=eiAt:=j=0∑N−1eiλjt∣uj⟩⟨uj∣
The quantum state of the register expressed in the eigenbasis of A is now
∑ j = 0 N − 1 b j ∣ λ j ⟩ n l ∣ u j ⟩ n b w h e r e ∣ λ j ⟩ n l \sum_{j=0}^{N-1} b _ { j } |\lambda _ {j }\rangle_{n_{l}} |u_{j}\rangle_{n_{b}} where |\lambda _ {j }\rangle_{n_{l}} ∑j=0N−1bj∣λj⟩nl∣uj⟩nbwhere∣λj⟩nl is the n_{l}-bit binary representation of λ j \lambda _ {j } λj.
Add an auxiliary qubit and apply a rotation conditioned on ∣ λ j ⟩ |\lambda_{ j }\rangle ∣λj⟩,
∑ j = 0 N − 1 b j ∣ λ j ⟩ n l ∣ u j ⟩ n b ( 1 − C 2 λ j 2 ∣ 0 ⟩ + C λ j ∣ 1 ⟩ ) \sum_{j=0}^{N-1} b _ { j } |\lambda _ { j }\rangle_{n_{l}}|u_{j}\rangle_{n_{b}} \left( \sqrt { 1 - \frac { C^{2} } { \lambda _ { j } ^ { 2 } } } |0\rangle + \frac { C } { \lambda _ { j } } |1\rangle \right) j=0∑N−1bj∣λj⟩nl∣uj⟩nb(1−λj2C2∣0⟩+λjC∣1⟩)
where C is a normalisation constant, and, as expressed in the current form above, should be less than the smallest eigenvalue λ m i n \lambda_{min} λmin in magnitude, i . e . , ∣ C ∣ < λ m i n i.e., |C| < \lambda_{min} i.e.,∣C∣<λmin.
Apply Q P E † QPE^{\dagger} QPE†. Ignoring possible errors from QPE, this results in
∑ j = 0 N − 1 b j ∣ 0 ⟩ n l ∣ u j ⟩ n b ( 1 − C 2 λ j 2 ∣ 0 ⟩ + C λ j ∣ 1 ⟩ ) \sum_{j=0}^{N-1} b _ { j } |0\rangle_{n_{l}}|u_{j}\rangle_{n_{b}} \left( \sqrt { 1 - \frac {C^{2} } { \lambda _ { j } ^ { 2 } } } |0\rangle + \frac { C } { \lambda _ { j } } |1\rangle \right) j=0∑N−1bj∣0⟩nl∣uj⟩nb(1−λj2C2∣0⟩+λjC∣1⟩)
Measure the auxiliary qubit in the computational basis. If the outcome is 1, the register is in the post-measurement state
( 1 ∑ j = 0 N − 1 ∣ b j ∣ 2 / ∣ λ j ∣ 2 ) ∑ j = 0 N − 1 b j λ j ∣ 0 ⟩ n l ∣ u j ⟩ n b \left( \sqrt { \frac { 1 } { \sum_{j=0}^{N-1} \left| b _ { j } \right| ^ { 2 } / \left| \lambda _ { j } \right| ^ { 2 } } } \right) \sum _{j=0}^{N-1} \frac{b _ { j }}{\lambda _ { j }} |0\rangle_{n_{l}}|u_{j}\rangle_{n_{b}} (∑j=0N−1∣bj∣2/∣λj∣21)j=0∑N−1λjbj∣0⟩nl∣uj⟩nb
which up to a normalisation factor corresponds to the solution.
We are almost there for ∣ x ⟩ = A − 1 ∣ b ⟩ = ∑ j = 0 N − 1 λ j − 1 b j ∣ u j ⟩ |x\rangle=A^{-1}|b\rangle=\sum_{j=0}^{N-1}\lambda_{j}^{-1}b_{j}|u_{j}\rangle ∣x⟩=A−1∣b⟩=∑j=0N−1λj−1bj∣uj⟩
Apply an observable M to calculate F ( x ) : = ⟨ x ∣ M ∣ x ⟩ F(x):=\langle x|M|x\rangle F(x):=⟨x∣M∣x⟩.
Quantum Phase Estimation (QPE) within HHL
Quantum Phase Estimation is described in more detail in Chapter 3. However, since this quantum procedure is at the core of the HHL algorithm, we recall here the definition. Roughly speaking, it is a quantum algorithm which, given a unitary U with eigenvector ∣ ψ ⟩ m |\psi\rangle_{m} ∣ψ⟩m and eigenvalue e 2 π i θ e^{2\pi i\theta} e2πiθ, finds θ \theta θ. We can formally define this as follows.
Definition: Let U ∈ C 2 m × 2 m U\in\mathbb{ C }^{2^{m}\times 2^{m}} U∈C2m×2m be unitary and let ∣ ψ ⟩ m ∈ C 2 m |\psi\rangle_{m}\in\mathbb{ C }^{2^{m}} ∣ψ⟩m∈C2m be one of its eigenvectors with respective eigenvalue e 2 π i θ e^{2\pi i\theta} e2πiθ. The Quantum Phase Estimation algorithm, abbreviated QPE, takes as inputs the unitary gate for U and the state ∣ 0 ⟩ n ∣ ψ ⟩ m |0\rangle_{n}|\psi\rangle_{m} ∣0⟩n∣ψ⟩m and returns the state ∣ θ ~ ⟩ n ∣ ψ ⟩ m . H e r e θ ~ |\tilde{\theta}\rangle_{n}|\psi\rangle_{m}. Here \tilde{\theta} ∣θ~⟩n∣ψ⟩m.Hereθ~ denotes a binary approximation to 2 n θ 2^{n}\theta 2nθ and the n subscript denotes it has been truncated to n digits.
QPE ( U , ∣ 0 ⟩ n ∣ ψ ⟩ m ) = ∣ θ ~ ⟩ n ∣ ψ ⟩ m \operatorname { QPE } ( U , |0\rangle_{n}|\psi\rangle_{m} ) = |\tilde{\theta}\rangle_{n}|\psi\rangle_{m} QPE(U,∣0⟩n∣ψ⟩m)=∣θ~⟩n∣ψ⟩m
For the HHL we will use QPE with U = e i A t U = e ^ { i A t } U=eiAt, where A is the matrix associated to the system we want to solve. In this case,
e i A t = ∑ j = 0 N − 1 e i λ j t ∣ u j ⟩ ⟨ u j ∣ e ^ { i A t } = \sum_{j=0}^{N-1}e^{i\lambda_{j}t}|u_{j}\rangle\langle u_{j}| eiAt=j=0∑N−1eiλjt∣uj⟩⟨uj∣
Then, for the eigenvector ∣ u j ⟩ n b |u_{j}\rangle_{n_{b}} ∣uj⟩nb, which has eigenvalue e i λ j t e ^ { i \lambda _ { j } t } eiλjt, QPE will output ∣ λ ~ j ⟩ n l ∣ u j ⟩ n b |\tilde{\lambda }_ { j }\rangle_{n_{l}}|u_{j}\rangle_{n_{b}} ∣λ~j⟩nl∣uj⟩nb. Where λ ~ j \tilde{\lambda }_ { j } λ~j represents an n l − b i t n_{l}-bit nl−bit binary approximation to 2 n l λ j t 2 π 2^{n_l}\frac{\lambda_ { j }t}{2\pi} 2nl2πλjt. Therefore, if each λ j \lambda_{j} λj can be exactly represented with n l n_{l} nl bits,
QPE ( e i A t , ∑ j = 0 N − 1 b j ∣ 0 ⟩ n l ∣ u j ⟩ n b ) = ∑ j = 0 N − 1 b j ∣ λ j ⟩ n l ∣ u j ⟩ n b \operatorname { QPE } ( e ^ { i A t } , \sum_{j=0}^{N-1}b_{j}|0\rangle_{n_{l}}|u_{j}\rangle_{n_{b}} ) = \sum_{j=0}^{N-1}b_{j}|\lambda_{j}\rangle_{n_{l}}|u_{j}\rangle_{n_{b}} QPE(eiAt,j=0∑N−1bj∣0⟩nl∣uj⟩nb)=j=0∑N−1bj∣λj⟩nl∣uj⟩nb
Reference: https://qiskit.org/textbook/ch-applications/hhl_tutorial.html