19. Dropout从零代码实现以及简洁实现

1. 从零实现

要实现单层的暂退法函数， 我们从均匀分布U[0,1]中抽取样本，样本数与这层神经网络的维度一致。 然后我们保留那些对应样本大于p的节点，把剩下的丢弃。

在下面的代码中，我们实现 dropout_layer 函数， 该函数以dropout的概率丢弃张量输入X中的元素， 如上所述重新缩放剩余部分：将剩余部分除以1.0-dropout。

import torch
from torch import nn
from d2l import torch as d2l


def dropout_layer(X, dropout):
    assert 0 <= dropout <= 1
    # 在本情况中，所有元素都被丢弃
    if dropout == 1:
        return torch.zeros_like(X)
    # 在本情况中，所有元素都被保留
    if dropout == 0:
        return X
    # torch.rand是从[0,1]均匀分布中随机抽取数据，返回张量
    mask = (torch.rand(X.shape) > dropout).float() # 这一句代码相当于对一个矩阵随机0或1
    return mask * X / (1.0 - dropout)

Q:解释一下得到mask的原理。

A：我的理解是，torch.rand(X.shape)得到的是一个和X一样大的张量，张量中每一个数都去和dropout比较，如果大于dropout就保留，置为true，经过float变为1. ，反之小于dropout的置为0。假设我令dropout=0.6，那么矩阵中大于0.6的项会置为1，小于0.6的项为0。

我当时存在一个疑惑就是，难道随机数在【0.6，1）之间才能留下嘛，那【0.2，0.6）之间的间距和【0.6，1）一样，为什么就不能留下。后面我想清楚是觉得，既然要以0.6的概率丢失一部分数据，那干脆控制变量使得小于0.6的数据为0，设定这样一个准则，这样torch.rand它是随机初始化的，也就是每一遍各个位置上的数据是随机的，那么从中选小于0.6的数据置为0就是在随机选取位置，使这个位置上的数据为0.

我之前总把目光着重于数据的比较，其实在这里随机选取的本质是数据所在的位置，而选择小于0.6 只是一种实现的方法。

因此，这样想通了之后，我再去看弹幕及评论说的“这里的dropout是数据丢失的概率，而不是比率，即使p=0.5，也有可能全部丢失或者全部保留”。

解释：因为如果是比率，那当然就是有一半的位置要空出来。但是如果是概率，则它是随机的，有可能通过torch.rand得到的张量的所有元素都是大于0.5的，或者都是小于0.5的，这样就和“以p概率丢失数据”说得通了。

关于torch.rand 和 torch.randn

这里的实现“以dropout的概率丢弃张量输入X中的元素“是先得到mask这一个bool矩阵，再去和输入的X相乘，而不是直接从X中随机选一些变为0，因为后一个方法对gpu和cpu都不是很好，做乘法远比选一个元素快。

---

我们可以通过下面几个例子来测试dropout_layer函数。 我们将输入X通过暂退法操作，暂退概率分别为0、0.5和1。

X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
print(X)
print(dropout_layer(X, 0.))
print(dropout_layer(X, 0.5))
print(dropout_layer(X, 1.))

ps：每一次运行的时候，会调用随机生成数，使得每一次被置为0的位置是随机的。（精髓所在）

2. 定义模型参数

使用 Fashion-MNIST数据集。 我们定义具有两个隐藏层的多层感知机，每个隐藏层包含256个单元。

num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256

3. 定义模型

我们可以将暂退法应用于每个隐藏层的输出（在激活函数之后）， 并且可以为每一层分别设置暂退概率： 常见的技巧是在靠近输入层的地方设置较低的暂退概率。 下面的模型将第一个和第二个隐藏层的暂退概率分别设置为0.2和0.5， 并且暂退法只在训练期间有效。

dropout1, dropout2 = 0.2, 0.5

class Net(nn.Module):
    def __init__(self,num_inputs,num_outputs,num_hiddens1,num_hiddens2, is_training=True):# 进行了重写
        super(Net,self).__init__()
        self.num_inputs = num_inputs
        self.training = is_training
        self.lin1 = nn.Linear(num_inputs,num_hiddens1)
        self.lin2 = nn.Linear(num_hiddens1,num_hiddens2)
        self.lin3 = nn.Linear(num_hiddens2,num_outputs)
        self.relu = nn.ReLU()
    
    def forward(self,X):
        H1 = self.relu(self.lin1(X.reshape(-1, self.num_inputs))) # 第一个隐藏层的输出
        # 只有在训练模型时才使用dropout
        if self.training == True:
            # 在第一个全连接层之后添加一个dropout层
            H1 = dropout_layer(H1, dropout1)
        H2 = self.relu(self.lin2(H1)) # 如果不是训练，在通过relu得到输出H2
        if self.training == True:
            # 在第二个全连接层之后添加一个dropout层
            H2 = drop_layer(H2,dropout2)
        out = self.relu(lin3(H2))
        return out
    
net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)

4. 训练和测试

这类似于前面描述的多层感知机训练和测试。

num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
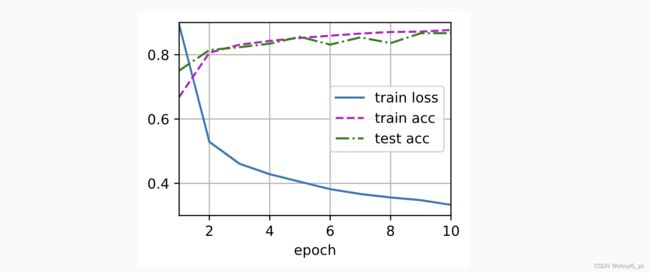
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

5. 简洁实现

对于深度学习框架的高级API，我们只需在每个全连接层之后添加一个Dropout层， 将暂退概率作为唯一的参数传递给它的构造函数。 在训练时，Dropout层将根据指定的暂退概率随机丢弃上一层的输出（相当于下一层的输入）。 在测试时，Dropout层仅传递数据。

net = nn.Sequential(nn.Flatten(),
        nn.Linear(784, 256),
        nn.ReLU(),
        # 在第一个全连接层之后添加一个dropout层
        nn.Dropout(dropout1),
        nn.Linear(256, 256),
        nn.ReLU(),
        # 在第二个全连接层之后添加一个dropout层
        nn.Dropout(dropout2),
        nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

接下来对模型进行训练和测试：

trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

运行结果如下：