学习百度Apollo中的决策规划

学习视频链接

无人车的任务：定位（在哪里）、感知（看到了什么）、预测（环境下一步怎么变化）、规划（我们应该怎么移动）、控制（怎样控制车辆）

一、无人车规划问题与解决框架

1.定义：

无人车规划问题就是控制车辆安全平稳地运行到终点。要求无人车需要遵守交通规则，计算模块的速率小于100ms（0.1s），还有保证一定的舒适性、平稳性，可以适应复杂的路况。

2.输入与输出：

接收从上游模块（如感知、定位、导航）获得的信息，生成一条无人车可以行驶的轨迹，交给下游模块（如控制）去执行。

具体来说，无人车规划问题的输入为：周围障碍物的信息、本车状态（一部分是来自底盘本身发出的关于方向盘转角等信息，另一部分是来自定位的输出）、交通灯信息、高精地图的信息（包含路径的信息，以及路径间的拓扑关系）、导航信息。

3.无人车规划模块的设计思路

①多策略并发机制

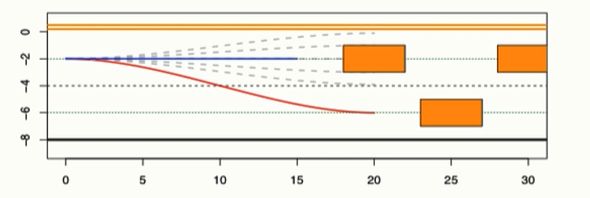
先进行不同道路策略上的规划，不同策略间相互独立，然后通过不同策略的比较选择最优。

②道路内规划

将道路信息整合在道路中心线构建的平滑坐标系上，找到满足交通规则的道路内最优解，还要满足性能上的优化。

若生成右图所示的路径，那么乘坐感会较差，因为在直线与转弯的交界处需要猛打方向盘。所以先根据道路中心线获得左图的若干小黑点，然后生成灰色的框，希望规划的路径尽可能平稳地穿过这个灰色的框，并且满足曲率2阶可导（这样就避免猛打方向盘了）。

③道路内规划的“硬约束”与“软约束”

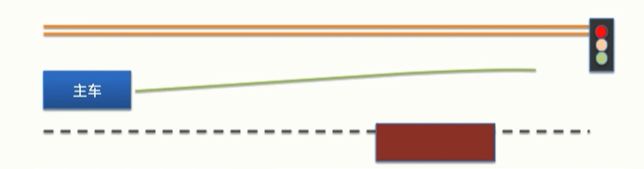
对于上图所示情景，主车想要给红车让道。那么硬约束就是诸如指示灯的要求、不能撞车等任何情况下都不能违背的交通规则，会将这些条件以规则的形式写入代码中；软约束就是人为决策，比如跟着红车，或者绕过红车，这些是通过动态优化策略去完成的。当已经完成人为决策之后，会通过基于样条的二次规划去生成一条平滑的轨迹。

4.无人车的规划模块架构

根据路网，对多条路径建立起多条参考线，即参考线的预选模块。
建立多个参考线之后，不同参考线之间建立起不同的参考系，不同的参考系内部进行路径规划。通过动态规划的方式去寻找软约束条件，再通过二次规划（QP）生成一条平稳的轨迹。也就是说，这是个动态规划和二次规划相结合的路径规划和速度规划结合的方式。

对于无人车的新框架的核心可以总结为三点：决策规划合二为一；换道策略分而治之；道路内规划要稳定，满足实效性。

二、决策规划中的优化问题

1.定义

决策规划中的优化问题一般是指道路内的优化问题。而道路内的规划问题其实是一个三维的规划：沿道路行驶的x方向坐标、横向坐标L、时间T，即为LST坐标。

根据EM（期望最大化）迭代的原理，将复杂的三维规划问题降维成速度规划问题和路径规划问题，然后不断将其进行迭代求解。
具体做法为：

基于道路内建立的平滑坐标系，对障碍物进行投影（SL投影，E step）；
投影完之后，生成一条最优的路径（M step）；
对于这条路径，把周围的障碍物在纵向和时间的平面上进行投影（ST投影， E step）；
在此平面内对无人车进行速度规划优化（M step）。

2.优化问题的三个关键点

①目标函数cost：对于无人车来说，是指各项指标的线性叠加。比如曲率的平滑率、安全性等。

②约束条件：满足交规，避免碰撞的前提条件

③优化求解

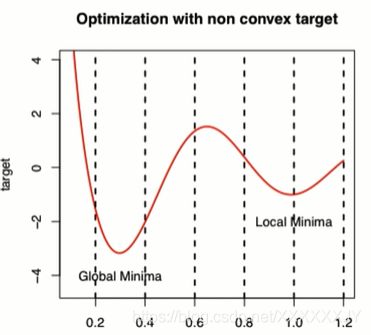
凸函数只有唯一的一个最优解，在我们求解时方便。
而上图就是一个非凸函数，也就是既有全局最优点，又有局部最优点。而目标是寻找全局最优解，解决这类非凸函数的优化问题的思路为：
Ⅰ 撒点获取粗略解。如在上图的0.2，0.4，0.6，0.8，1.0，1.2的位置撒点，获取函数在这些点上的数值，从而获得函数的粗略解。对应规划模块的动态规划算法（DP）。
Ⅱ 二次优化QP获得精确解。基于上述获得的粗略解，进行二次样条获取全局最优解。对应规划模块的二次样条（QP）。

3.planning

①路径规划

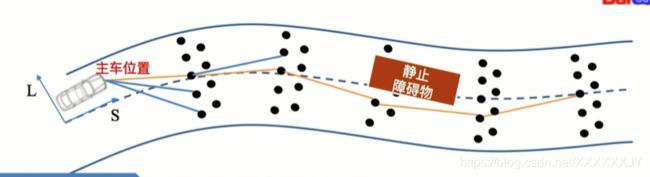
通过道路中心线建立的SL坐标上，从主车位置出发向前方撒若干排点；利用动态规划的方式，设置目标函数，进行动态规划的求解；然后通过折线的方式连接出一条粗略的解。

②路径QP算法
即基于路径的二次规划算法

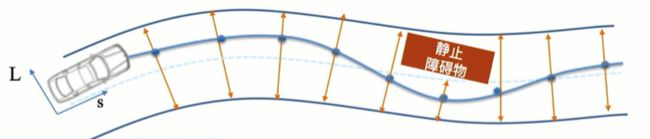
当已经有了粗略解，知道对于这个静态障碍物，需要从下方绕过它时，对于纵向坐标s取若干个控制的位置，在这些位置处获取能走的上下界的范围，如上图中橘红色的可行区域。这就是二次规划问题的约束条件。将曲率和曲率连续性，贴近中心线等作为约束条件。这样就将整个问题转化为一个凸问题。

③速度规划

生成一条无人车可以行驶的路径之后，需要对无人车的速度进行规划。

首先将周围障碍物投影到需要行进的路上。
若一辆车出现在主车前方时，路径方向的s方向和时间t组成的st图中，就会形成上方所示的遮盖区域，表示生成的曲线必须存在于遮盖区域的下方，即跟着前车开。
若一辆车比较慢，在主车后方时，会形成图中下面的框，表明应该通过一些方式绕开那辆车。

然后类似于路径规划，先粗略找到图中红色线所在处的粗略解。

④速度QP算法

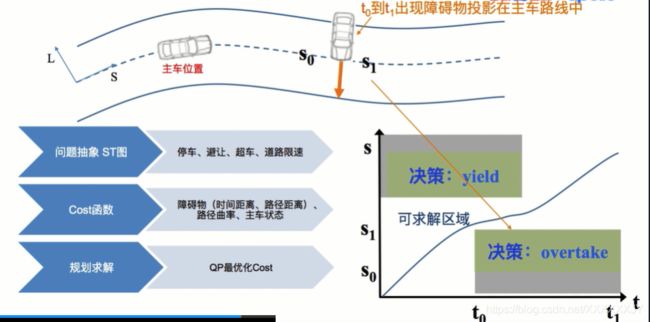
得到速度规划的粗略解之后，需要进行二次规划算法。具体做法为：
当获得粗略解之后，就可以在图中获得一个可求解区域（在这个可求解区域内，是凸的），并且我们不可以穿过上面的阴影区，也不能低于下面的阴影区。
同样也需要用到二次规划的样条算法去求解。

总结一下，也就是路径和速度算法的不断迭代，在不断迭代的过程中下层的速度算法在进行下一周期的路径规划时也会有相应的影响。不断EM迭代的过程，在内部，速度和路径算法就分成了一个动态规划和二次规划的结合，从而可以解决二维平面中的非凸问题。二次规划算法主要的作用就是生成一条平滑的可避开障碍物的轨迹，从而交给车辆的控制模块去平稳运行。