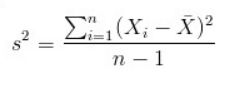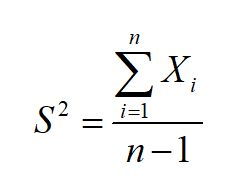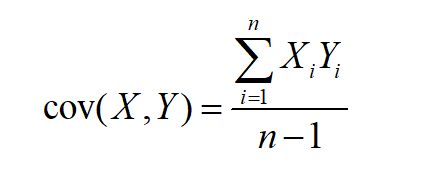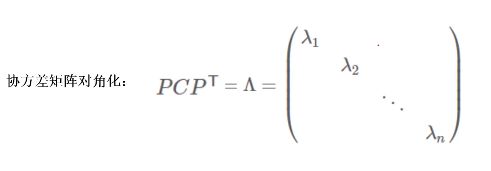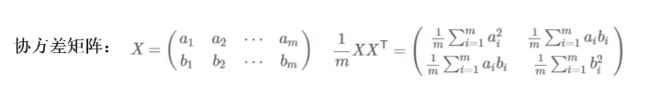数据挖掘与机器学习————降维之主成分分析法(PCA,Principal components analysis )
1.概述
PCA(Principal components analysis)
是一种降维方法、一种线性变换。这个变换主要是利用正交变换(基变换),将数据变换到一个新的坐标系中,使得原本难以分割的数据变得好分割,即线性无关。
2.数学基础
内积(又名点积、数量积、标量积)、方差、协方差、实对称矩阵、对角化、正交矩阵、正交变换、特征值以及特征向量的求法。
①方差:
方差表现了数据的离散程度,方差越大,数据就越离散。
如果对数据中心化,即均值为0,则方差表示为
②协方差:
中心化,变为:
样本的两个特征之间的协方差越大,则越相关,在图形表示上就越相互交叉(从而越要使之分离)。因此在PCA中,最终应该使得协方差为0,从而使之线性无关,在图形表示上看起来容易分割。
③实对称矩阵
n阶矩阵A,其元素均为实数,并且转置等于本身,则A为实对称矩阵。
一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量,即该矩阵必定可以对角化。
E=(e1,e2,……,en)
④ 对角化
对角化是指存在一个正交矩阵A,使得![]() 成为一个对角矩阵(只有对角为非0元素),相似对角矩阵上的元素为矩阵本身的特征值,并且在对角线上按照元素大小从上到下排列。
成为一个对角矩阵(只有对角为非0元素),相似对角矩阵上的元素为矩阵本身的特征值,并且在对角线上按照元素大小从上到下排列。
⑤正交矩阵
如果![]() (E为单位矩阵)或
(E为单位矩阵)或![]() ,则n阶实矩阵A称为正交矩阵。
,则n阶实矩阵A称为正交矩阵。
⑤特征向量与特征值
利用特征分解得到特征值与特征向量,特征向量总结了特征,特征值表示特征的重要程度,特征值越大则特征就越重要。
3. 算法原理
在不断理解算法的过程中,我们会不断地提出问题,因此本文主要通过提出问题的方式来讲解算法原理。
值得注意的是,理解算法前,应首先浏览前部分的数学基础,以方便理解这段内容。
首先的问题是,为什么要降维?换句话说,为什么要进行坐标变换?
降维,顾名思义,很大程度是为了降低维度,但是核心是进行坐标变换,将二维的空间映射到一维的空间,将高维的空间映射到低维的空间。而其实常常忽略另一个重要的因素,有些特征与其他特征融合在一起(具有一定相关性),在原坐标系下不易被分割(分类),因此需要进行变换。
那么问题又来了,如何进行变换呢?
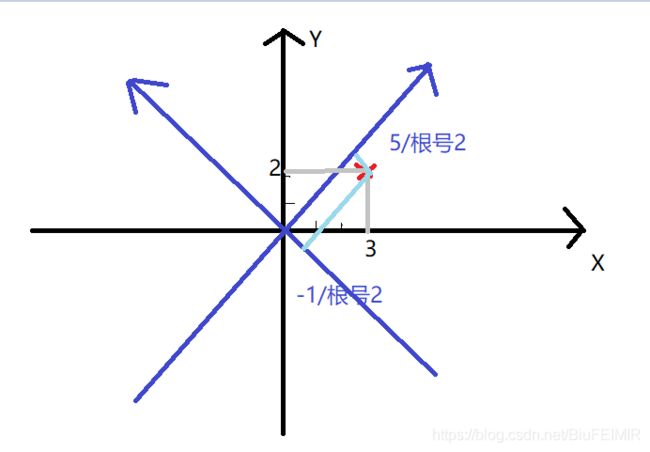
以二维直角坐标系为例,我们知道基可以表示坐标系,如(1,0)和(0,1)就是一对基。基是正交的,即内积为0,或者说相互垂直。不同的坐标系,在同一空间的基不同。我们可以在当前坐标系下,确定另外一组基,从而建立新的坐标系,从而进行变换。举例说明,具体变换。比如在原坐标系有一点(3,2),重新确定了一组基为(-1,1)(1,1),注意单位化,则为(![]() ,
,![]() )(
)(![]() ,
,![]() ),将其进行矩阵运算。
),将其进行矩阵运算。
要知道正交基无数,如何确定最合适的那组基呢?
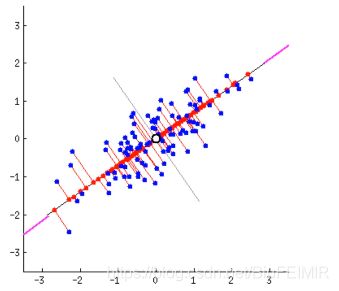
确定基,应再次明确我们的目标————使得数据便于分割----->使得数据离散---->使得数据在新坐标系方差最大(协方差为0,使得数据特征之间线性无关)。
看下图,更方便理解(看点离线的距离,第一个图方差小,第二图方差大)。
因此需要构建协方差矩阵,求得协方差为0情况下的特征值,从而求得特征向量,进而得到新坐标系下的基。
协方差矩阵形式如下图所示:
该图表示,共有m个样本点,a、b两种特征,的二维数据。因此降维只能降成一维的,并且仅需找到一个新的基(n维降成k维需要找k个新的基)。矩阵对角线的元素为对应字段的方差,其他元素为a与b的协方差。需要注意的是,这里的数据X进行了中心化,中心化后的方差和协方差才如图中矩阵表示。如果不清楚一定要查看前面提到的数学基础。
4. 案例
5. Python代码
##Python实现PCA
import numpy as np
def pca(X,k):#k is the components you want
#mean of each feature
n_samples, n_features = X.shape
mean=np.array([np.mean(X[:,i]) for i in range(n_features)])
#normalization
norm_X=X-mean
#scatter matrix
scatter_matrix=np.dot(np.transpose(norm_X),norm_X)
#Calculate the eigenvectors and eigenvalues
eig_val, eig_vec = np.linalg.eig(scatter_matrix)
eig_pairs = [(np.abs(eig_val[i]), eig_vec[:,i]) for i in range(n_features)]
# sort eig_vec based on eig_val from highest to lowest
eig_pairs.sort(reverse=True)
# select the top k eig_vec
feature=np.array([ele[1] for ele in eig_pairs[:k]])
#get new data
data=np.dot(norm_X,np.transpose(feature))
return data
X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
print(pca(X,1))
参考资料
[1]优化神器:机器学习经典算法-PCA降维算法
https://www.bilibili.com/video/BV1CJ41117nw?from=search&seid=11840436996735703538
[2] 协方差 https://www.zhihu.com/question/20852004
[3] 实对称矩阵及其他性质 https://blog.csdn.net/qq_24690701/article/details/81839016
[4] 代码参考 https://blog.csdn.net/program_developer/article/details/80632779