C语言AI五子棋(大一新生)
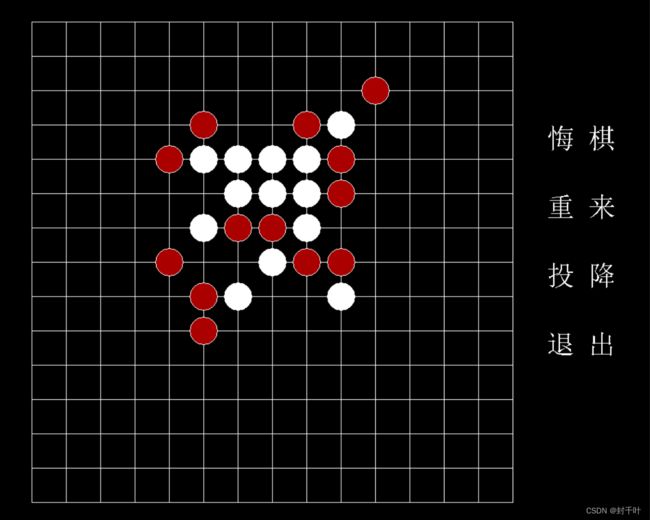
该游戏为C语言所编写的基于easy-x图形库的程序,有基本C语言知识即可理解。该游戏用极大极小搜索实现AI执棋,棋力与一般人相当。运行需提前安装好easy-x图形库,文末有完整源码。
代码运行结果
主体实现思想
//开局
void begin(struct point p[25][25])
{
board(); //棋盘图形背景加载
while (1)
{
if (/*按下鼠标左键*/)
{
if (/*鼠标坐标在悔棋区域*/)
{
//悔棋
}
if (/*鼠标坐标在重开区域*/)
{
//重开
}
if (/*鼠标坐标在投降区域*/)
{
//投降
}
if (/*鼠标坐标在退出区域*/)
{
//退出
}
if (/*鼠标坐标在棋盘上*/) //玩家执棋
{
fillcircle(m.x, m.y, 20); //在该位置画红圆
p[i][j].state = -1; //修改该位置的状态
/*判断胜负*/
robot(p); //电脑执棋,在某位置画白圆
/*判断胜负*/
}
}
}
}
电脑AI执棋方法
首先,我们先来认识一下极大极小搜索。在该算法中,我们需要定义一个评估函数,该评估函数能够给出当前局面对于电脑的优势程度,并以具体数字呈现,数字越大该局面对电脑越有利,越小则对玩家越有利。如下图所示,假设当前局面为p1并且轮到电脑方下棋,p3为p1走两步后产生的所有局面的优势分。p1时轮到电脑方下棋,电脑希望能从p2中找到优势分最大的那一步,但是,此时p2的分数又是未知的,因为对弈比的是最终结果,而不是当前结果,上一层的分数都由下一层来决定。因此我们需要先确定p2的分数,p2轮到玩家下棋,他肯定是希望从p3中选择分数最小的那一步,当然p3的分数是由评估函数确定出来的。我们可以以此类推,确定要搜索的深度,最底层的分数由评估函数得出,然后依次往上推。
p2为玩家执棋,从p3中选最小值,分别为7,5,4。
p1为电脑执棋,从p2中选最大值,为7。
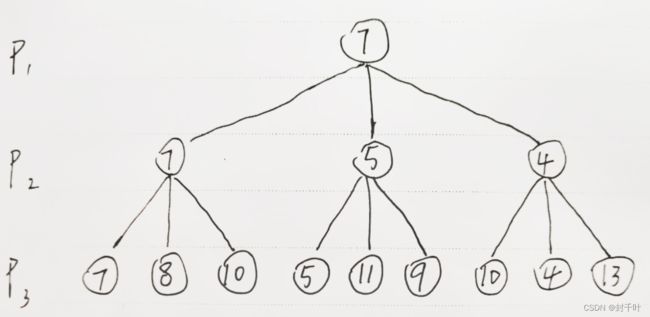
极大极小搜索伪代码如下:
//电脑执棋
int robot(struct point p[25][25])
{
for (i = MIN; i < MAX; i++) //寻找最佳落子点
{
for (j = MIN; j < MAX; j++)
{
if (p[i][j].state == 0) //该点为空
{
p[i][j].state = 1; //假设电脑下在这里
p[i][j].n_value = deduction(p, 1, 1, A, B); //获取下一步分数
p[i][j].state = 0; //撤回
if (p[i][j].n_value > v) //v初始值为无穷小
{
v = p[i][j].n_value; //找最大值
x = i;
y = j; //获取坐标
}
}
}
}
/*执行坐标x,y */
return 0;
}
//递归推演
double deduction(struct point p[25][25], int sex, int depth, long double a, long double b)
{
if (depth == 0 || end(p) != 0) //达到深度或棋局结束
{
return assess(p); //递归出口,返回评估函数的分数
}
else if (sex % 2 == 1) //玩家回合
{
for (m = MIN; m < MAX; m++)
{
for (n = MIN; n < MAX; n++)
{
if (p[m][n].state == 0) //为空
{
p[m][n].state = -1; //假设棋下在这个地方
va = deduction(p, sex + 1, depth - 1, a, b); //获取下一步分数
p[m][n].state = 0; //撤回
if (va < b) //找最小值
{
b = va;
}
}
}
}
return b; //返回分数
}
else if (sex % 2 == 0) //电脑回合
{
for (m = MIN; m < MAX; m++)
{
for (n = MIN; n < MAX; n++)
{
if (p[m][n].state == 0 && t != 0) //为空
{
p[m][n].state = 1; //棋下在这个地方
va = deduction(p, sex + 1, depth - 1, a, b); //获取下一步分数
p[m][n].state = 0; //撤回
if (va > a) //找最大值
{
a = va;
}
}
}
}
return a;//返回分数
}
}
至此,电脑已经可以找出“最好”的棋位了,但是由于博弈树呈指数增长,计算量过大,因此需要对算法进行优化,以加深搜索深度。我们可进行对博弈树α-β剪枝。看下图,假设我们已经在p21从p31中选了最小值7,在p22求分数时我们又在p32中发现了5,这时,我们可以对p22进行剪枝,即跳出p22的搜索循环。因为我们在p32中发现了5,因此p22的分数肯定不大于5,又因为p21的分数为7>5,而p1是要从p2中找最大值的,因此肯定不会是p2中的分数,因此可以对p2进行剪枝。找到p33中的4时也是一样,因为p21的值7>4,所以发现p33的4时,可对p23进行剪枝跳出p23的搜索循环.
 我们还可以对一些不必要的点进行剪枝,比如那些周围没有一个子的点,算法很简单,对位置周围进行搜索,全为空时剪掉即可。加了剪枝的代码如下:
我们还可以对一些不必要的点进行剪枝,比如那些周围没有一个子的点,算法很简单,对位置周围进行搜索,全为空时剪掉即可。加了剪枝的代码如下:
//电脑执棋
int robot(struct point p[25][25])
{
int i, j, x = 0, y = 0,m, n, t = 0;
long double v = -999999999999999999; //10^18
for (i = MIN; i < MAX; i++) //寻找最佳落子点
{
for (j = MIN; j < MAX; j++)
{
if (p[i][j].state == 0 ) //为空
{
t = 0;
for (m = -1; m < 2; m++) {
for (n = -1; n < 2; n++) {
if (p[i + m][j + n].state != 0) {
t++; //偏僻点剪枝
}
}
}
if (t != 0) //不偏僻
{
p[i][j].state = 1; //假设电脑下在这里
p[i][j].n_value = deduction(p, 1, 1, A, B);
p[i][j].state = 0; //撤回
if (p[i][j].n_value > v)
{
v = p[i][j].n_value; //找最大值
x = i;
y = j; //获取坐标
}
}
}
}
}
setfillcolor(WHITE); //填充颜色
fillcircle((x + 1 - MIN) * 50, (y + 1 - MIN) * 50, 20);//画圆,下这一步
xx = x;
yy = y; //为悔棋坐标做记录
p[x][y].state = 1; //修改状态
return 0;
}
//递归推演
double deduction(struct point p[25][25], int sex, int depth, long double a, long double b)
{
int m, n,i, j, t = 0,br=0;
long double va = 0;
if (depth == 0 || end(p) != 0) //达到深度或棋局结束
{
return assess(p); //递归出口,返回分数
}
else if (sex % 2 == 1) //玩家回合
{
for (m = MIN; m < MAX; m++)
{
if (br == 1) { //b剪枝
break;
}
for (n = MIN; n < MAX; n++)
{
if (p[m][n].state == 0 ) //为空
{
if (num < 40) {
t = 0;
for (i = -1; i < 2; i++) {
for (j = -1; j < 2; j++) {
if (p[i + m][j + n].state != 0) {
t++; //偏僻点剪枝
}
}
}
}
else {
t = 1;
}
if (t == 0) //偏僻
{
va = B;
}
else {
p[m][n].state = -1; //棋下在这个地方
va = deduction(p, sex + 1, depth - 1, a, b);
p[m][n].state = 0; //撤回
}
if (va < b) //找最小值
{
b = va;
}
if (b < a)
{
break; //b剪枝
br = 1;
}
}
}
}
return b; //返回分数
}
else if (sex % 2 == 0) //电脑回合
{
for (m = MIN; m < MAX; m++)
{
if (br == 1) { //a剪枝
break;
}
for (n = MIN; n < MAX; n++)
{
if (p[m][n].state == 0 ) //为空
{
if (num < 40) {
t = 0;
for (i = -1; i < 2; i++) {
for (j = -1; j < 2; j++) {
if (p[i + m][j + n].state != 0) {
t++; //偏僻点剪枝
}
}
}
}
else {
t = 1;
}
if (t == 0) //偏僻
{
va = A;
}
else {
p[m][n].state = 1; //棋下在这个地方
va = deduction(p, sex + 1, depth - 1, a, b);
p[m][n].state = 0; //撤回
}
if (va > a) //找最大值
{
a = va;
}
if (b < a)
{
break; //a剪枝
br = 1;
}
}
}
}
return a;//返回分数
}
return 0;
}
想要让电脑具有更高的棋力,还需要有一个好的评估函数。我们可以用if语句对不同的情况进行赋分。笔者所用的是对每个点进行赋分,空点价值为0,红子和白子取相反数,每个点有8个方向的延伸价值,每个方向为5分,被敌方或边界挡住即为0;每两个相同的子连在一起则他们的分数乘一定的倍数,还有距离中心的优势分等等,详见完整代码。此仅做参考,读者可自行设计出更加科学、计算量更少的评估函数。
完整代码以及详细注释
#define _CRT_SECURE_NO_WARNINGS
#include<graphics.h>
#include<Windows.h>
#include<conio.h>
#include <math.h>
#include<time.h>
#include<mmsystem.h>
#include<easyx.h>
#include<iostream>
#include<stdlib.h>
using namespace std;
#define E 10 // E=防守/攻击
#define V 10 //位置初始分以及倍率
#define MIN 5
#define MAX 20
long double A = -999999999999999999;
long double B = 999999999999999999;
int ii = 0, jj = 0, xx = 0, yy = 0; //记录上一步棋位置
int num = 0; //对弈次数
void board(); //绘画棋盘
void regret(struct point p[25][25]); //悔棋
void begin(struct point p[25][25]); //开始
int robot(struct point p[25][25]); //电脑执棋
void over(int x); //结束界面
void p_assess(struct point p[25][25]); //某点价值分评定
double assess(struct point p[25][25]); //局面优势评估
double deduction(struct point p[25][25], int sex, int depth, long double a, long double b);//递归推演
int end(struct point p[25][25]); //胜负代数返回
void initialize(struct point p[25][25]); //棋盘初始化
void execute(struct point p[25][25],int x,int y); //下棋
struct point {
int state; //位置的状态 玩家-1, 空位置0, 电脑1
long double value; //该点价值分
long double n_value; //下一步棋下这点时棋盘的总优势分
};
//初始化
void initialize(struct point p[25][25])
{
int i, j;
num = 0;
for (i = 0; i < 25; i++)
{
for (j = 0; j < 25; j++)
{
p[i][j].state = 0; //为空
p[i][j].value = 0;
p[i][j].n_value = 0;
}
}
}
//胜负代数返回
int end(struct point p[25][25])
{
int i, j, k = 0, x = 0, y = 0, b = 0, q = 0, e = 0;
for (i = MIN; i < MAX; i++)
{
for (j = MIN; j < MAX; j++)
{
if (p[i][j].state == 0)
{
k++;
if (k == 0)
{
e = 1;//平局
}
}
if (p[i][j].state)
{
for (x = -2; p[i][j].state == p[i][j + x].state && x < 4; x++) //横
{
}
for (y = -2; p[i][j].state == p[i + y][j].state && y < 4; y++) //纵
{
}
for (b = -2; p[i][j].state == p[i + b][j + b].state && b < 4; b++) //斜下
{
}
for (q = -2; p[i][j].state == p[i - q][j + q].state && q < 4; q++) //斜上
{
}
if (x == 3 || y == 3 || b == 3 || q == 3)
{
if (p[i][j].state == 1)
{
e = 2; //玩家输
}
if (p[i][j].state == -1)
{
e = 3; //玩家赢
}
}
}
}
}
return e; //e=0默认未结束
}
//绘画棋盘
void board()
{
initgraph(950, 800);//初始化绘图窗口
setbkcolor(BLACK);//绘图背景色
cleardevice();//使用当前背景色清空上一个绘图
setlinecolor(WHITE);//设置当前设备画线颜色
for (int i = 50; i <= 750; i += 50)//画棋盘
{
line(i, 50, i, 750);
line(50, i, 750, i);
}
setlinecolor(RED);//设置当前设备画线颜色
settextstyle(40, 0, "宋体");
outtextxy(800, 200, "悔 棋");
outtextxy(800, 300, "重 来");
outtextxy(800, 400, "后 手");
outtextxy(800, 500, "退 出");
settextcolor(RED);
settextstyle(15, 0, "宋体");
outtextxy(2, 2, "作者:杨秀杰");
}
//下棋
void execute(struct point p[25][25], int x, int y)
{
setfillcolor(WHITE); //填充颜色
fillcircle((x + 1 - MIN) * 50, (y + 1 - MIN) * 50, 20);//画圆,下这一步
xx = x;
yy = y; //为悔棋坐标做记录
p[x][y].state = 1; //修改状态
}
//悔棋
void regret(struct point p[25][25])
{
board();
setrop2(R2_COPYPEN); //设置绘制颜色
setcolor(WHITE);
p[ii][jj].state = 0; //将上一步棋清空
p[xx][yy].state = 0;
for (int i = MIN; i < MAX; i++) { //重新绘制棋盘
for (int j = MIN; j < MAX; j++) {
if (p[i][j].state == -1) {
setfillcolor(RED);
fillcircle((i + 1-MIN) * 50, (j + 1-MIN) * 50, 20);
}
if (p[i][j].state == 1) {
setfillcolor(WHITE);
fillcircle((i + 1-MIN) * 50, (j + 1-MIN) * 50, 20);
}
}
}
}
//开局
void begin(struct point p[25][25])
{
MOUSEMSG m; // 定义鼠标消息
int x, y, i, j;
board(); //图形背景加载
setlinecolor(WHITE); //设置当前设备画线颜色
while (1)
{
m = GetMouseMsg();//获取鼠标信息
x = m.x % 50;
y = m.y % 50;
setrop2(R2_COPYPEN); //二元光栅操作码:R2_COPYPEN当前颜色
if (m.uMsg == WM_LBUTTONDOWN) //按下鼠标左键
{
if (m.x <= 900 && m.y < 250 && m.x >= 800 && m.y > 200) //悔棋
{
regret(p);//悔棋
continue;
}
if (m.x <= 900 && m.y < 350 && m.x >= 800 && m.y > 300) //重开
{
initialize(p); //初始化
begin(p);
}
if (m.x <= 900 && m.y < 450 && m.x >= 800 && m.y > 400) //后手
{
if (num < 1)
{
robot(p); //电脑执棋
num++;
}
}
if (m.x <= 900 && m.y < 550 && m.x >= 800 && m.y > 500) //退出
{
closegraph(); // 关闭绘图窗口
exit(0); //强制退出
}
if (x >= 25) //玩家执棋
m.x = m.x - x + 50;
else
m.x = m.x - x;
if (y >= 25)
m.y = m.y - y + 50;
else
m.y = m.y - y;
i = m.x / 50 - 1+ MIN; //坐标转换
j = m.y / 50 - 1+ MIN;
if (i < 20 && j < 20)
{
if (p[i][j].state==-1)
break;
if (m.x <= 750 && m.y <= 750 && m.x >= 50 && m.y >= 50)
{
setfillcolor(RED);//设置当前设备画线颜色
fillcircle(m.x, m.y, 20); //在该位置画圆下棋
ii = i; //为悔棋坐标做记录
jj = j;
p[i][j].state = -1;//修改该位置的状态
}
if (end(p) != 0)//结束判断
{
Sleep(1000);
over(end(p));//结束界面
}
robot(p); //电脑执棋
if (end(p) != 0)//结束判断
{
Sleep(1000);
over(end(p));//结束界面
}
num++; //对弈次数
}
}
}
}
//结束界面
void over(int x)
{
point pp[25][25]; // 5--19
initialize(pp); //初始化
initgraph(400, 400);
cleardevice(); //使用当前背景色清空绘图设备
settextstyle(50, 24, "宋体");
settextcolor(RED); //字体颜色
if (x == 1)
{
outtextxy(100, 50, "平局");
}
else if (x == 2)
{
outtextxy(100, 50, "电脑获胜");
}
else if(x==3)
{
outtextxy(100, 50, "玩家获胜");
}
settextcolor(WHITE);
outtextxy(50, 200, "返回游戏界面");
outtextxy(80, 300, " 结束游戏");
while (true)
{
MOUSEMSG n;//鼠标信息
n = GetMouseMsg();
switch (n.uMsg) {
case WM_LBUTTONDOWN:
if (n.x <= 350 && n.x >= 50 && n.y <= 250 && n.y >= 200)
begin(pp); //返回游戏界面
if (n.x <= 300 && n.x >= 80 && n.y <= 350 && n.y >= 300)
{
closegraph(); // 关闭绘图窗口
exit(0); //强制退出
}
}
}
}
//局面优势评估
double assess(struct point p[25][25])
{
int i, j;
p_assess(p); //某点价值评定
long double s_value = 0;
for (i = MIN; i < MAX; i++)
{
for (j = MIN; j < MAX; j++)
{
s_value += p[i][j].value;//棋盘总优势分为所有点分数的和
}
}
return s_value;
}
//某点价值评定
void p_assess(struct point p[25][25])
{
int i, j, k, m, n, x, y;
for (i = MIN; i < MAX; i++) //可改进为米字刷新
{
for (j = MIN; j < MAX; j++)
{
if (p[i][j].state == 0)
{
p[i][j].value = 0; //空位价值为零
}
else //不为空
{ //8个方向每个价值为10
long double v1 = V, v2 = V, v3 = V, v4 = V, v5 = V, v6 = V, v7 = V, v8 = V;
//****************************************************************************
for (x = 0, n = j; p[i][j].state != -p[i][n + 1].state && n + 1 < 20 && x < 4; x++, n++) //右
{
}
if (x < 4)
{
v1 = 0; //被挡住为0
}
else {
for (k = 0, n = j; p[i][j].state == p[i][n + 1].state && k < 5; k++, n++) //右
{
v1 *= V; //连续分数翻倍
}
}
for (y = 0, n = j; p[i][j].state != -p[i][n - 1].state && n - 1 > 4 && y < 4; y++, n--) //左
{
}
if (y < 4)
{
v2 = 0; //被挡住为0
}
else {
for (k = 0, n = j; p[i][j].state == p[i][n - 1].state && k < 5; k++, n--) //左
{
v2 *= V; //连续分数翻倍
}
}
//****************************** 以下同上 ***************************************
for (x = 0, n = i; p[i][j].state != -p[n + 1][j].state && n + 1 < 20 && x < 5; x++, n++) //上
{
}
if (x < 4)
{
v3 = 0; //被挡住为0
}
else {
for (k = 0, n = i; p[i][j].state == p[n + 1][j].state && k < 5; k++, n++) //上
{
v3 *= V; //连续分数翻倍
}
}
for (y = 0, n = i; p[i][j].state != -p[n - 1][j].state && n - 1 > 4 && y < 5; y++, n--) //下
{
}
if (y < 4)
{
v4 = 0; //被挡住为0
}
else {
for (k = 0, n = i; p[i][j].state == p[n - 1][j].state && k < 5; k++, n--) //下
{
v4 *= V; //连续分数翻倍
}
}
//********************************** 以下同上 **************************************
for (x = 0, m = i, n = j; p[i][j].state != -p[m - 1][n + 1].state && n + 1 < 20 && m - 1 > 4 && x < 5; x++, m--, n++) //右上
{
}
if (x < 4)
{
v5 = 0; //被挡住为0
}
else {
for (k = 0, m = i, n = j; p[i][j].state == p[m - 1][n + 1].state && k < 5; k++, m--, n++) //右上
{
v5 *= V; //连续分数翻倍
}
}
for (y = 0, m = i, n = j; p[i][j].state != -p[m + 1][n - 1].state && m + 1 < 20 && n - 1 > 4 && y < 5; y++, m++, n--) //左下
{
}
if (y < 4)
{
v6 = 0; //被挡住为0
}
else {
for (k = 0, m = i, n = j; p[i][j].state == p[m + 1][n - 1].state && k < 5; k++, m++, n--) //左下
{
v6 *= V; //连续分数翻倍
}
}
//*********************************** 以下同上 **************************************
for (x = 0, m = i, n = j; p[i][j].state != -p[m - 1][n - 1].state && n - 1 > 4 && m - 1 > 4 && x < 5; x++, m--, n--) //左上
{
}
if (x < 4)
{
v7 = 0; //被挡住为0
}
else {
for (k = 0, m = i, n = j; p[i][j].state == p[m - 1][n - 1].state && k < 5; k++, m--, n--) //左上
{
v7 *= V; //连续分数翻倍
}
}
for (y = 0, m = i, n = j; p[i][j].state != -p[m + 1][n + 1].state && n + 1 < 20 && m + 1 < 20 && y < 5; y++, m++, n++) //右下
{
}
if (y < 4)
{
v8 = 0; //被挡住为0
}
else {
for (k = 0, m = i, n = j; p[i][j].state == p[m + 1][n + 1].state && k < 5; k++, m++, n++) //右下
{
v8 *= V; //连续分数翻倍
}
}
//********************************************************************************
p[i][j].value = v1 + v2 + v3 + v4 + v5 + v6 + v7 + v8 + 0.1 * (15 - abs(i - 12) - abs(j - 12)); //加上距离中心优势分
if (p[i][j].state == -1) //玩家棋子为负分
{
p[i][j].value = -p[i][j].value * E; //E为偏向防守程度
}
}
}
}
}
//递归推演
double deduction(struct point p[25][25], int sex, int depth, long double a, long double b)
{
int m, n,i, j, t = 0,br=0;
long double va = 0;
if (depth == 0 || end(p) != 0) //达到深度或棋局结束
{
return assess(p); //递归出口,返回分数
}
else if (sex % 2 == 1) //玩家回合
{
for (m = MIN; m < MAX; m++)
{
if (br == 1) { //b剪枝
break;
}
for (n = MIN; n < MAX; n++)
{
if (p[m][n].state == 0 ) //为空
{
if (num < 80) {
t = 0;
for (i = -1; i < 2; i++) {
for (j = -1; j < 2; j++) {
if (p[i + m][j + n].state != 0) {
t++; //偏僻点剪枝
}
}
}
}
else {
t = 1;
}
if (t == 0) //偏僻
{
va = B;
}
else {
p[m][n].state = -1; //棋下在这个地方
va = deduction(p, sex + 1, depth - 1, a, b);
p[m][n].state = 0; //撤回
}
if (va < b) //找最小值
{
b = va;
}
if (b < a)
{
break; //b剪枝
br = 1;
}
}
}
}
return b; //返回分数
}
else if (sex % 2 == 0) //电脑回合
{
for (m = MIN; m < MAX; m++)
{
if (br == 1) { //a剪枝
break;
}
for (n = MIN; n < MAX; n++)
{
if (p[m][n].state == 0 ) //为空
{
if (num < 80) {
t = 0;
for (i = -1; i < 2; i++) {
for (j = -1; j < 2; j++) {
if (p[i + m][j + n].state != 0) {
t++; //偏僻点剪枝
}
}
}
}
else {
t = 1;
}
if (t == 0) //偏僻
{
va = A;
}
else {
p[m][n].state = 1; //棋下在这个地方
va = deduction(p, sex + 1, depth - 1, a, b);
p[m][n].state = 0; //撤回
}
if (va > a) //找最大值
{
a = va;
}
if (b < a)
{
break; //a剪枝
br = 1;
}
}
}
}
return a;//返回分数
}
return 0;
}
//电脑执棋
int robot(struct point p[25][25])
{
int i, j, x = 12, y = 12,m, n, t = 0;
long double v = -999999999999999999; //10^18
for (i = MIN; i < MAX; i++) //寻找最佳落子点
{
for (j = MIN; j < MAX; j++)
{
if (p[i][j].state == 0 ) //为空
{
t = 0;
for (m = -1; m < 2; m++) {
for (n = -1; n < 2; n++) {
if (p[i + m][j + n].state != 0) {
t++; //偏僻点剪枝
}
}
}
if (t != 0) //不偏僻
{
p[i][j].state = 1; //假设电脑下在这里
if (end(p) == 2)
{
execute(p, i, j); //下棋
return 0;
}
p[i][j].n_value = deduction(p, 1, 2, A, B);
p[i][j].state = 0; //撤回
if (p[i][j].n_value > v)
{
v = p[i][j].n_value; //找最大值
x = i;
y = j; //获取坐标
}
}
}
}
}
execute(p, x, y); //下棋
return 0;
}
int main()
{
point p[25][25]; // 棋盘大小15*15 边界为5
initialize(p); //初始化
begin(p); //开局
return 0;
}