【Python算法】数值分析—拉格朗日插值法（2-已知原函数做拟合分析）——附源码
一、背景
拉格朗日插值法可在未知原函数，只知道节点值、节点函数值时，以多项式的形式拟合出原函数。它也可以在已知原函数的情况下，对拟合出的多项式进行分析，进一步讨论多项式次数、插值区间大小对拟合出的多项式的精度影响。
对于未知原函数，拟合后做预测的讨论，请移步拉格朗日插值法（1-原函数未知做预测）
拟合出的多项式：
而
、
是已知量，是实际容易测得的值，如一天内的时间和温度值，其拟合出的
就是温度关于时间变化的函数表达式
二、函数逻辑（function文件，完整代码在文末）
主要步骤：
- 计算
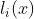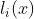的分子 - 计算的分母
- 通过 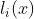的分子分母组合出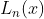
- 分别计算多项式和原函数在同一点的值，做比较
1.给定区间两点及划分次数，求出区间列表
def get_list_x(a, # 左区间
b, # 右区间
n # 区间n等分
):
if a < b:
return np.linspace(a, b, n)
else:
return np.linspace(b, a, n) 2.计算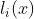的分子
def get_li_numerator(list_x):
""" 计算li(x)的分子部分，返回分子的表达式 """
x = sp.symbols('x')
numerator = [1 for _ in range(0, len(list_x))] # 初始化分子列表，全置为1
for i in list(range(0, len(list_x))):
for j in list(range(0, len(list_x))):
# 循环计算到自己时，跳过此次循环
if j == i:
continue
value_item = x - list_x[j]
numerator[i] = numerator[i] * value_item
return numerator 3.计算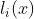的分母
def get_li_denominator(list_x):
""" 计算li(x)的分母部分 """
denominator = [1 for _ in range(0, len(list_x))] # 初始化分母列表，全置为1
for i in list(range(0, len(list_x))):
for j in list(range(0, len(list_x))):
# 循环计算到自己时，跳过此次循环
if j == i:
continue
value_item = list_x[i] - list_x[j]
denominator[i] = denominator[i] * value_item
return denominator 4.组合出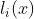的表达式
def get_expression_li(list_x):
""" 计算li(x)的表达式 """
# 获取分子表达式
numerator = get_li_numerator(list_x)
# 获取分母的数值列表
denominator = get_li_denominator(list_x)
# 初始化li的表达式列表
expression_li = []
for i in list(range(0, len(numerator))):
expression_li.append(numerator[i] / denominator[i])
return expression_li5.组合出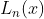表达式
def get_expression_lagrange(list_fx, list_x):
""" 获取拉格朗日差值多项式的表达式 """
# 获取li(x)的表达式
expression_li = get_expression_li(list_x)
# 初始化拉格朗日插值多项式为0
expression_lagrange = 0
for i in list(range(0, len(list_x))):
expression_lagrange += expression_li[i] * list_fx[i]
return expression_lagrange6.计算原函数在x点的值
def get_value_fx(fx, x,
precision=5 # 计算保留的有效数字
):
""" 计算fx的值 """
return fx.evalf(subs={'x': x}, n=precision)7.计算拟合出的多项式在x点的值
def get_value_expression_lagrange(expression_lagrange, # 拉格朗日差值多项式的表达式
x, # 某一点x
precision=5 # 计算保留的有效数字
):
""" 计算拉格朗日差值多项式在某一点x的值 """
return expression_lagrange.evalf(subs={'x': x}, n=precision)三、最终实现（main文件，完整代码）
import function as fun
import sympy as sp
x = sp.symbols('x')
# 设置原函数
fx = 1/(1+x**2)
# 给定区间及等分次数，获取对应x列表
list_x = fun.get_list_x(-5, 5, 5)
# 设置待计算的点
interpolation_x = 0
# 获取拉格朗日插值多项式
expression_lagrange = fun.get_expression_lagrange(fx, list_x)
# 计算该多项式在计算点的值
result_interpolation = fun.get_value_expression_lagrange(expression_lagrange, interpolation_x)
result_true = fun.get_value_fx(fx, interpolation_x)简单输出结果
print("原始表达式：", fx)
print("拉格朗日插值多项式：", expression_lagrange)
print("插值结果：", result_interpolation)
print("真值结果：", result_true)部分结果展示
function文件完整代码
import numpy as np
import sympy as sp
def get_list_x(a, # 左区间
b, # 右区间
n # 区间n等分
):
if a < b:
return np.linspace(a, b, n)
else:
return np.linspace(b, a, n)
def get_li_numerator(list_x):
""" 计算li(x)的分子部分，返回分子的表达式 """
x = sp.symbols('x')
numerator = [1 for _ in range(0, len(list_x))] # 初始化分子列表，全置为1
for i in list(range(0, len(list_x))):
for j in list(range(0, len(list_x))):
# 循环计算到自己时，跳过此次循环
if j == i:
continue
value_item = x - list_x[j]
numerator[i] = numerator[i] * value_item
return numerator
def get_li_denominator(list_x):
""" 计算li(x)的分母部分 """
denominator = [1 for _ in range(0, len(list_x))] # 初始化分母列表，全置为1
for i in list(range(0, len(list_x))):
for j in list(range(0, len(list_x))):
# 循环计算到自己时，跳过此次循环
if j == i:
continue
value_item = list_x[i] - list_x[j]
denominator[i] = denominator[i] * value_item
return denominator
def get_expression_li(list_x):
""" 计算li(x)的表达式 """
# 获取分子表达式
numerator = get_li_numerator(list_x)
# 获取分母的数值列表
denominator = get_li_denominator(list_x)
# 初始化li的表达式列表
expression_li = []
for i in list(range(0, len(numerator))):
expression_li.append(numerator[i] / denominator[i])
return expression_li
def get_value_fx(fx, x,
precision=5 # 计算保留的有效数字
):
""" 计算fx的值 """
return fx.evalf(subs={'x': x}, n=precision)
def get_expression_lagrange(fx, list_x,
precision=5 # 计算保留的有效数字
):
""" 获取拉格朗日差值多项式的表达式 """
# 获取li(x)的表达式
expression_li = get_expression_li(list_x)
# 初始化拉格朗日插值多项式为0
expression_lagrange = 0
for i in list(range(0, len(list_x))):
value_fx = get_value_fx(fx, list_x[i], precision)
expression_lagrange += expression_li[i] * value_fx
return expression_lagrange
def get_value_expression_lagrange(expression_lagrange, # 拉格朗日差值多项式的表达式
x, # 某一点x
precision=5 # 计算保留的有效数字
):
""" 计算拉格朗日差值多项式在某一点x的值 """
return expression_lagrange.evalf(subs={'x': x}, n=precision)demo源码链接如下
github地址：https://github.com/method_lagrange_interpolation
gitee地址：https://gitee.com/darlingxyz/method_lagrange_interpolation